Parametric Modeling & Simulation Modes in EM.Cube
Contents
- 1 The Variety of Simulation Modes in EM.Cube
- 2 Running Frequency Sweep Simulations in EM.Cube
- 3 EM.Cube Variables
- 4 Running Parametric Sweep Simulations in EM.Cube
- 5 Running Monte Carlo Simulations in EM.Cube
- 6 Generating Surrogate Models
- 7 Performing Optimization in EM.Cube
- 7.1 Planning for Optimization
- 7.2 Understanding the Design Objectives
- 7.3 Defining Design Objectives
- 7.4 EM.Cube's Optimization Algorithms
- 7.5 Defining the Optimization Variables & Other Settings
- 7.6 Running a Single-Objective Optimization Simulation
- 7.7 Building the Error Function for a Multivariable Optimization
The Variety of Simulation Modes in EM.Cube
EM.Cube's computational modules offers different simulation modes for different purposes. The simplest simulation mode is analysis, single-frequency analysis or wideband analysis. All of these three modes involve a single run of the simulation engine, which takes the mesh of the physical structure "As Is". EM.Ferma's analysis mode simulates the structure at DC or under quasi-static assumption. The single-frequency analysis modes of EM.Terrano, EM.Illumina, EM.Picasso and EM.Libera simulate the physical structure at the center frequency of the project. EM.Tempo's wideband analysis mode first simulates the physical structure in the time domain and then computes its frequency domain characteristics at a number of frequency samples within the specified bandwidth of the project. All the other simulation modes involve multiple simulation engine runs. In the case of EM.Terrano's frequency sweep, the more time consuming geometrical optics ray tracing analysis is carried out once independent of the operational frequency and the electromagnetic quantities are computed at all the specified frequency samples. In that respect, this mode may qualify as single-run.
The table below lists all the available simulation modes in EM.Cube's various computational modules:
| Simulation Mode | Usage | Number of Engine Runs | Frequency | Supporting Module(s) |
|---|---|---|---|---|
| Single-Frequency Analysis | Simulates the physical structure "As Is" | Single run | Runs at the center frequency fc | EM.Terrano, EM.Picasso, EM.Libera, EM.Illumina |
| Wideband Analysis | Simulates the physical structure "As Is" | Single run | Generates data for many frequency samples within the specified project bandwidth | EM.Tempo |
| Static Analysis | Simulates the physical structure "As Is" | Single run | Runs at DC or under quasi-static assumption | EM.Ferma |
| Frequency Sweep | Varies the operating frequency of the solver | Multiple runs | Runs at a specified set of frequency samples or adds more frequency samples in an adaptive way | EM.Terrano, EM.Picasso, EM.Libera, EM.Illumina |
| Parametric Sweep | Varies the value(s) of one or more project variables | Multiple runs | Runs at the center frequency fc or DC | EM.Tempo, EM.Terrano, EM.Ferma, EM.Picasso, EM.Libera, EM.Illumina |
| Optimization | Optimizes the value(s) of one or more project variables to achieve a design goal | Multiple runs | Runs at the center frequency fc or DC | EM.Tempo, EM.Ferma, EM.Picasso, EM.Libera, EM.Illumina |
| HDMR Sweep | Varies the value(s) of one or more project variables to generate a compact model | Multiple runs | Runs at the center frequency fc | EM.Tempo, EM.Picasso, EM.Libera, EM.Illumina |
| Dispersion Sweep | Varies the value of wavenumber in a periodic structure | Multiple runs | Runs at multiple frequency points corresponding to constant wavenumber values | EM.Tempo |
For a detailed description of each simulation mode, please refer to the manuals of individual computational modules under the sections titled "Running Simulations".
Running Frequency Sweep Simulations in EM.Cube
Uniform Frequency Sweep
In a frequency sweep, the operating frequency of your project is varied during each sweep run. Since the center frequency of your project is controlled by a default variable called fc, you can always sweep fc in lieu of a dedicated frequency sweep. In that case, you can even perform multivariable sweep simulations, whereby the frequency and other variables vary simultaneously.
Four of EM.Cube's computational modules provide an automated frequency sweep as one of their simulation modes. These are:
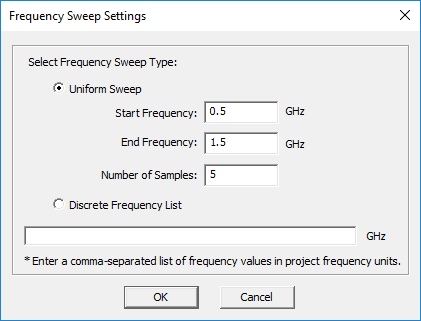
An automated frequency sweep is a single-variable sweep and cannot be combined with other variables. In a uniform frequency sweep, the frequency range and the number of frequency samples are specified. The samples are equally spaced over the frequency range. At the end of each individual frequency run, the output data are collected and stored. At the end of the frequency sweep, the 3D data can be visualized and/or animated, and the 2D data can be plotted s. frequency in EM.Grid graphs.
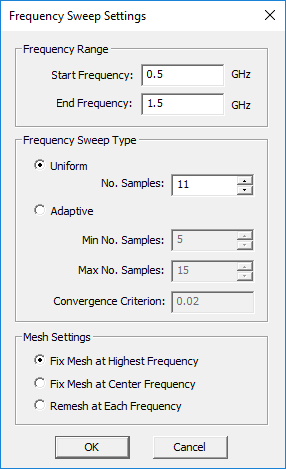
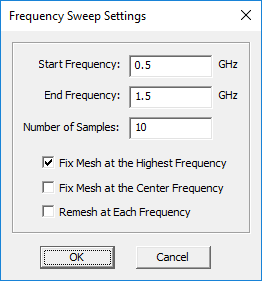
To run a uniform frequency sweep, open the Simulation Run dialog and select the Frequency Sweep option from the drop-down list labeled Simulation Mode. When you choose the frequency sweep option, the Settings button next to the simulation mode drop-down list becomes enabled. Clicking this button opens the "Frequency Sweep Settings" dialog. Set the values of Start Frequency, End Frequency and Number of Samples in this dialog.
During a frequency sweep in EM.Picasso, EM.Libera or EM.Illumina, the project's frequency changes at each sweep run, and so does the operating wavelength. As a result, the default mesh of the structure also changes at each frequency sample because its density is expressed in cells per effective wavelength. The frequency sweep settings dialogs of EM.Picasso, EM.Libera and EM.Illumina give you three choices regarding the mesh of the physical structure during a frequency sweep:
- Fix Mesh at the Highest Frequency
- Fix Mesh at the Center Frequency
- Re-Mesh at Each Frequency
The first option is the default choice which provides more accurate and smoother results for reasonable frequency ranges. However, if your sweep frequency range is very large and you fix the mesh of your structure at the highest frequency, it may lead to an unnecessarily large computational problem at the lower frequencies.
Adaptive Frequency Sweep
Frequency sweeps are often performed to study the frequency response of a given structure. In particular, the variation of scattering parameters like S11 (return loss) and S21 (insertion loss) with frequency are of primary interest. When analyzing resonant structures like patch antennas or filters over large frequency ranges, you may have to sweep a large number of frequency samples to capture their behavior with adequate details. The resonant peaks or notches are often missed due to the lack of adequate resolution. EM.Picasso and EM.Libera offer a powerful adaptive frequency sweep option for this purpose. It is based on the fact that the frequency response of a physical, causal, multiport network can be represented mathematically using a rational function approximation. In other words, the S-parameters of a circuit exhibit a finite number of poles and zeros over a given frequency range. An adaptive sweep first starts with very few frequency samples and tries to fit rational functions of low orders to the scattering parameters. Then, it increases the number of samples gradually by inserting intermediate frequency samples in a progressive manner. At each iteration cycle, all the possible rational functions of higher orders are tried out. The process continues until adding new intermediate frequency samples does not improve the resolution of the "Sij" curves over the given frequency range. In that case, the curves are considered as having converged.
You must first define one or more ports for your physical structure before you run an adaptive frequency sweep. Open the Frequency Sweep Settings dialog from the Simulation Run dialog and select the Adaptive option for Frequency Sweep Type. You have to set values for Minimum Number of Samples and Maximum Number of Samples. Their default values are 5 and 15, respectively. You also set a value for the Convergence Criterion, which has a default value of 0.02. At each iteration cycle, all the S parameters are calculated at the newly inserted frequency samples, and their average deviation from the curves of the last cycle is measured as an error. When this error falls below the specified convergence criterion, the iteration is ended. If EM.Cube reaches the specified maximum number of iterations and the convergence criterion has not yet been met, the program will ask you whether to continue the process or exit it and stop.
Cases of Failure of Adaptive Sweep
The results of adaptive sweep simulations are continuous and smooth most of the time. This is due to the fact that a rational function curve is fitted through the discrete frequency data points. This usually captures frequency response characteristics such as resonances with much fewer calculated data points. However, you have to make sure that the process converges. Otherwise, you might get an entirely wrong, but still perfectly smooth, graph at the end of the simulation.
For larger frequency ranges, you may have to increase both the minimum and maximum number of samples. For example, consider starting with 5 initial samples. The next iteration will insert 4 intermediate (midpoint) samples to have a total of 9 frequency samples. Note that all the previously computed samples are used in each progressive iteration. In the next iteration, 8 midpoint samples are inserted for a total of 17 samples. The next iteration will add 16 new samples for a total of 33 samples. If you start with M initial samples, then at the kth iteration, you will have a total of 2k(M-1) + 1 frequency samples.
EM.Cube's adaptive sweep algorithm computes a rational approximation of the S-parameter data in the following form:
- [math] H(s) = \frac{N(s)}{D(s)} = \frac{ \sum_{m=0}^{N} b_m s^m }{ \sum_{n=0}^{N+1} a_n s^n } [/math]
where 2N + 1 = 2k(M-1) + 1, which works well when the initial number of samples M is an odd number. In other words, the highest-order rational function is fitted at each iteration. As the total number of frequency samples grows at each subsequent iteration, the rational interpolation scheme might become unstable and produce spurious spikes. For this reason, when EM.Cube reaches the specified maximum number of iterations and the convergence criterion has not yet been met, you may choose to exit the loop and stop.
As an alternative to the automated adaptive sweep, you may perform a uniform sweep with a reasonable number of frequency samples (neither too few, nor too excessive) and then use EM.Cube's Smart Fit utility to fit a rational approximation of arbitrary order to the generated S-parameter data.
![]() Click here to learn more about Rational Interpolation of Port Characteristics.
Click here to learn more about Rational Interpolation of Port Characteristics.
EM.Cube Variables
What Are Variables For?
Variables provide the foundation for EM.Cube's parametric CAD modeling environment. A variable is a mathematical entity with a numeric value, which can be changed at any time. EM.Cube has two types of variables: independent and dependent. An independent variable is one that is defined by an initial numeric value. You can change the numeric value of an independent variable either manually or through a number of automated processes like parametric sweep, optimization, etc. A dependent variable, on the other hand, is defined by a mathematical expression that may involve other existing variables. The numeric value of a dependent variable is always determined by evaluating the mathematical expression that defines it.
Consider the following example:
x = 1
y = x
z = x+y
s = sp.j0(x)
t = s/t**2
In the above example, x is an independent variable, while y, z, s and t are all dependent variables. You can define an unlimited number of independent and dependent variables in EM.Cube. Note that precedence is important in the definition of variables. You should first define all the independent variables that are going to be used in the definition of a dependent variable.
You can use a large number of standard and advanced library functions to create expressions when defining dependent variables. You can use the basic arithmetic operations: addition "+", subtraction "-", multiplication "*", division "/", as well as the right and left parentheses "(" and ")" as delimiters. For raising powers, you can either use the power function pow(x,y) or simply use the symbol "**", e.g. "x**y". Use the constant "pi" as a reserved name to denote the Pi number π = 3.1415926..., and use the constant "e" as a reserve name to denote the Euler number e = 2.7182818... or the base of natural logarithm. You can also use any user-defined Python function in the definition of dependent variables.
![]() Click here to see a List of Library Functions.
Click here to see a List of Library Functions.
![]() Click here to learn more about Python's Standard & Advanced Mathematical Functions.
Click here to learn more about Python's Standard & Advanced Mathematical Functions.
![]() Click here to learn more about Creating Custom Python Functions.
Click here to learn more about Creating Custom Python Functions.
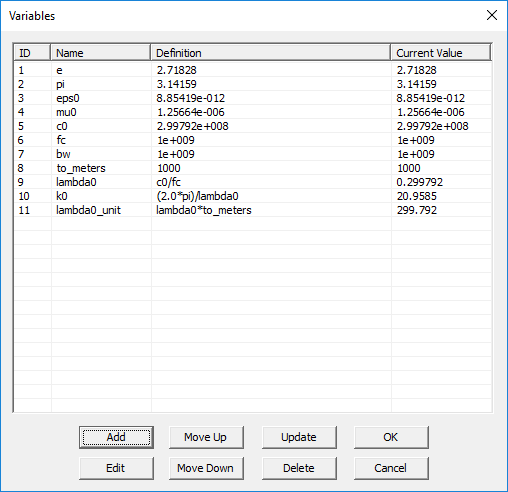
EM.Cube's Default Project Variables
When you start EM.Cube, it has a number of default variables that are associated with the general attributes of your project. These are listed in the table below:
| Variable Name | Definition | Usage |
|---|---|---|
| e | 2.71828 | Constant: The Euler number |
| pi | 3.14159 | Constant: The Pi (π) number |
| eps0 | 8.854e-012 | Constant: The free-space permittivity |
| mu0 | 1.257e-006 | Constant: The free-space permeability |
| c0 | 2.99792e+008 | Constant: The free-space speed of light |
| fc | 1e+009 | project center frequency in Hz |
| bw | 1e+009 | project bandwidth in Hz |
| to_meters | 1000 | conversion factor from the current project units to meter |
| lambda0 | c0/fc | the operating free-space wavelength in meters |
| k0 | (2.0*pi)/lambda0 | the operating free-space wavenumber in m-1 |
| lambda0_unit | lambda0*to_meters | the operating free-space wavelength in the current project units |
You can associate variables with almost any numeric quantity or parameter in EM.Cube such as the properties of geometric objects (coordinates, rotation angles, dimensions, etc.) or material properties of object groups and background structure, source properties, project frequency, mesh density, and unit cell periods in the case of periodic structures.
"fc" is perhaps EM.Cube's most important variable. It is tied to your project's center frequency. If you change the value of fc, the project's center frequency will change. Similarly, if you change the project's center frequency from the Frequency dialog or during a frequency sweep, the value of fc will also change accordingly. "lambda0" and lambda0_unit" are other useful variables widely used by most of EM.Cube wizards. These variables can be used to parameterize your physical structure in a frequency-scaled manner.
Defining a New Variable
You can define a new variable in EM.Cube either in formal manner using its Variables Dialog or directly from the property dialog of various objects. First, we discuss the "formal" manner. Follow the steps below to define a new variable:
- Open EM.Cube's Variables Dialog by clicking the Variables
 button of the Simulate Toolbar or selecting Menu → Simulate → Variables... or using the keyboard shortcut Ctrl+B.
button of the Simulate Toolbar or selecting Menu → Simulate → Variables... or using the keyboard shortcut Ctrl+B.
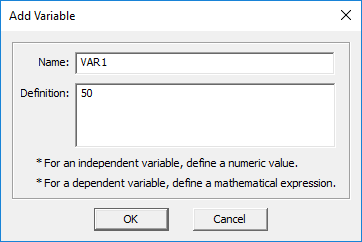
- To add a new variable, click the Add button to open the "Add Variable" dialog. Choose a Name for your new variable.
- In the box labeled Definition, define your new variable either as an independent variable with a numeric value or as a dependent variable using a mathematical expression that involves previously defined variables.
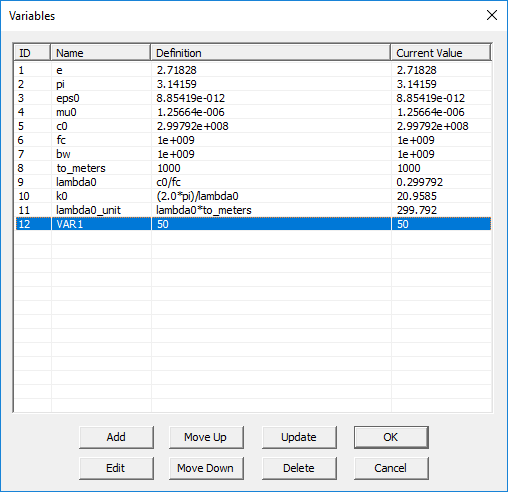
- Close the "Add Variable" dialog and return to the variables dialog. You will see the name and definition of your new variable added to the variables list.
You can select any variable from the list and edit its definition using the Edit button of the variables dialog at any time. Note that defining a variable simply adds it to EM.Cube's variables list. In order for a variable to be useful and do something, you have to associate it with the properties of actual objects or the general project properties.
Associating Variables with Object Properties
In most places where you see a numeric value for a parameter in any property dialog, e.g. the length of a rectangle strip object or the offset of a lumped or gap source on a line object, you can replace the numeric value with a variable. In that case, that parameter or quantity becomes tied up with the associated variable. This means that every time you change the value of a variable, the values of all of its associated object parameters or project properties will change accordingly. You can associate a variable with more than one object property and there is no limit in that respect.
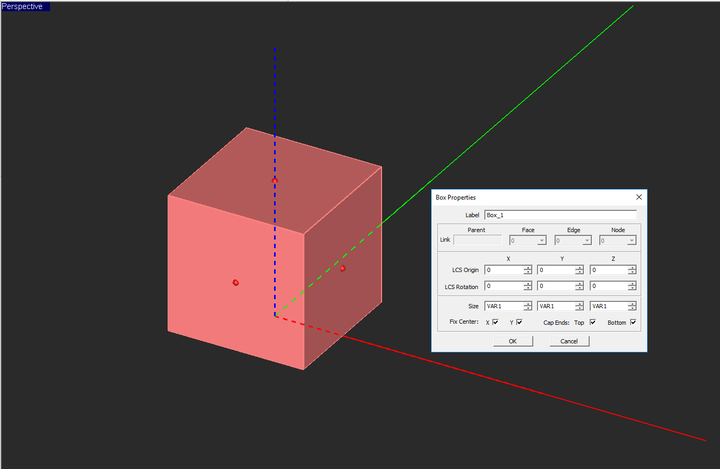
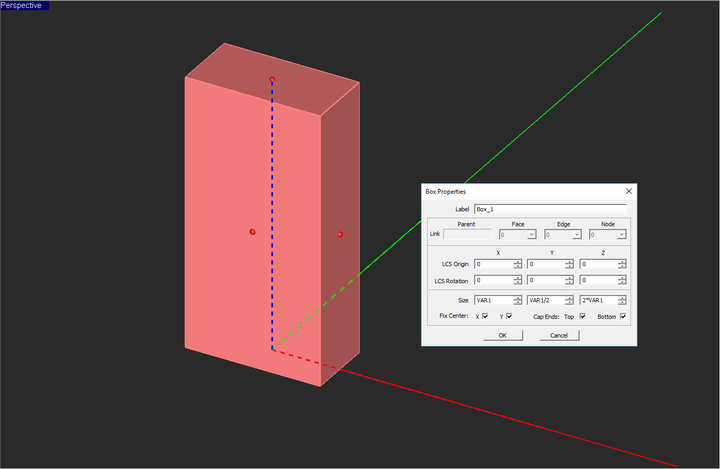
You can replace the numeric value of an object property either with a variable's name directly or with a mathematical expression using the names of the currently available variables. In the examples shown in the figures below, the X, Y and Z dimensions of a box object are replaced by the new variable VAR1 or expressions involving this variable.
| |
After changing a variable's value in the variables dialog, you may have to update your changes in the project workspace using the Update button of this dialog. |
Alternatively, you can define new variables directly from the property dialog of geometric objects or many other EM.Cube dialogs. If you replace the numeric value of a parameter with a text string, two things may happen. If the text string is already the name of an existing variable in the project's variables list, that parameter will be associated with the existing variable and the object who owns that parameter will be adjusted accordingly. If the text string has not already been used as the name of any variable, a new independent variable by that name is then created and added to EM.Cube's variables list. The numeric value of the modified parameter at the time of replacement is taken as both "Definition" and "Current Value" of the newly created independent variable.
The Scope of EM.Cube Variables
Every variable of your EM.Cube project has a global scope throughout that project. In other words, the name of every variable is regarded as a reserved name that is recognized by all of EM.Cube modules and utilities. If you use a mathematical expression that involves the name of a variable or a Python function that uses the name of a variable as its argument, the current value of that variable will be used for evaluation of that expression or function.
EM.Cube's variables list and its Python command line are synchronized. When you define and add a new independent or dependent variable in EM.Cube's variables dialog, it will be recognized in the Python command line. You can simply type the name of the variable at the command line and press the Enter key to execute the command, and you will see the current value of that variable in the command window. On the other hand, if you execute a variable assignment like x = 5 at the command line, a new variable called "x" with a definition of "5" is added to the variables list in the variables dialog. If you next type y = 2*x at the command line, the expression (2*x) will be evaluated first, and a new variable called "y" with a definition of "10" is then added to the variables list. However, if you type z = "2*x" at the command line, the text string "2*x" will be taken as the definition of the new variable "z" and will be reflected in the variables dialog. In other words, x and y are considered independent variables, while z is considered a dependent variable by the variables dialog.
Running Parametric Sweep Simulations in EM.Cube
Parametric Sweep as a Set of Successive Simulation Runs
Parametric sweep is a type of simulation where the values of one or more variables are varied in an automated manner during the course of the simulation. The variables whose values are varied are called the sweep variables. The rest of your project variables maintain their "current values" during a sweep simulation. If you have N sweep variables, then a complete set of N-tuples of the sweep variable samples is constructed. For each N-tuple (combination of variable values), the entire structure in your project workspace is updated, and so are all the other project properties that have been tied to the sweep variables. Each N-tuple requires an individual simulation engine run. Before the start of each simulation run, the mesh of the physical structure is regenerated. At the end of a parametric sweep simulation, all the sweep variables are reset to their original values in the variables dialog, as if the changes during the parametric sweep never took place.
In a parametric sweep, you have to choose your sweep variables from the pool of your project variables. Only independent variables are qualified to be designated as a sweep variable. This is expected because you cannot vary the value of a dependent variable freely. You can select one or more independent variables as sweep variables and specify how they should vary (be sampled) during the sweep simulation process.
Specifying Sweep Variables
To define a sweep variable and run a parametric sweep, follow the procedure below:
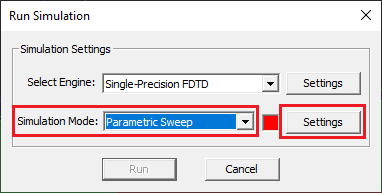
- Open the Simulation Run Dialog of any of EM.Cube's computational modules, and select the Parametric Sweep option from the dropdown list labeled Simulation Mode.
- When you choose the parametric sweep option, the Settings button next to the simulation mode dropdown list becomes enabled. Click this button to open up the Parametric Sweep Settings dialog.
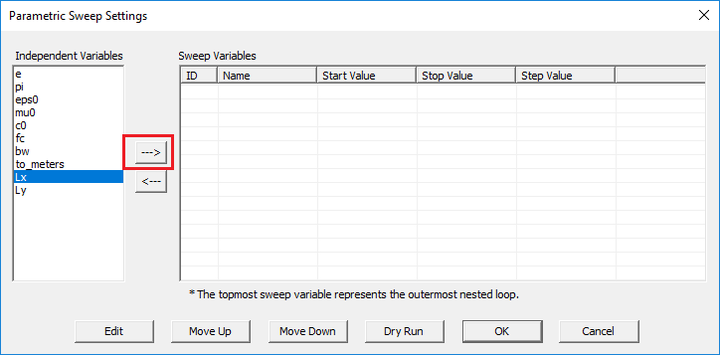
- On the left side of the dialog you see the "'Independent Variables Table", which lists all the available independent variables of your project. Select an independent variable from the table and use the Right Arrow (-->) button of the dialog to move it to the Sweep Variables List.
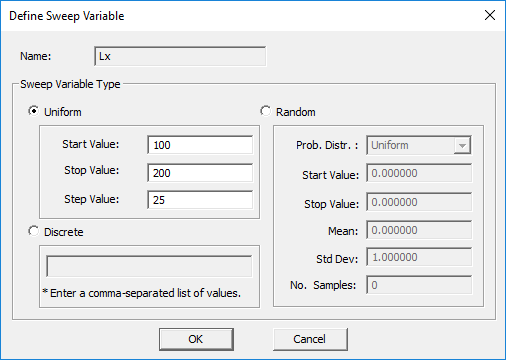
- Before moving the variable to the new location, the "Define Sweep Variable Dialog" opens up, where you have to define the attributes of your new sweep variable, e.g. its start, stop and step values.
- Once you finish the definition of a sweep variable, its name and attributes are added to the Sweep Variables List.
Note that you can change your mind and remove a sweep variable from the list. To do so, select its name or row from the list and use the Left Arrow (<--) button to move it back to the Independent Variables Table. You can also change the attributes of a sweep variable after it has been defined. Select the variable and click the Edit button of the dialog. After you are satisfied with the choice and definition of all your sweep variables, close the Parametric Sweep Settings dialog to return to the Run dialog, where you can start the Parametric Sweep simulation by clicking the Run ![]() button.
button.
The Variety of Sweep Variable Types
EM.Cube provides three types of sweep variables:
- Uniform sweep variable
- Discrete sweep variable
- Random sweep variable
The most widely used sweep simulation type is a uniform sweep. In this case, the value of a sweep variable is incremented from a "start value" to a "stop value" at a specified "step value". Depending on how you define the step value, the sweep process may get close to the stop value but miss the exact stop value before termination. You can also define a discrete sweep variable, whereby you specify the individual values of the sweep variable in a comma-separated list. The random variable will be discussed below in the context of Monte Carlo simulations in EM.Cube.
Sweep Simulation's Output Data Files
In a parametric sweep simulation, the geometrical or physical properties of one or more objects are changed during each sweep run, and the results of specified observables are collected in ASCII output data files. After the completion of a parametric sweep, you will see as many 3D output plots as the total number of variable samples under various nodes under various nodes of the Navigation Tree like sensors, current distributions, far fields, etc. Only the total field plots are saved on the Navigation Tree. You can run an animation of these 3D plots.
On the other hand, besides all the 2D data files with .DAT, .CPX and .ANG file extensions you would normally expect at the end of a basic analysis simulation, you will get additional similar data files with a "_Sweep" suffix in their names. These file contain the results of the sweep simulation process. They contain as many rows as the number of samples of the sweep variable(s). The left columns(s) represent the samples of the sweep variable(s) and the last column(s) on the right hold the computed values of standard or custom output parameters for each variable sample.
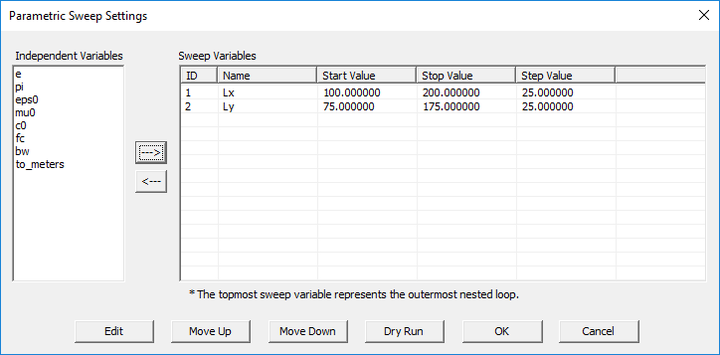
Multivariable Sweep Simulations
If you define two or more sweep variables, the sweep simulation process will then involve nested sweep loops that follow the order of definition of the sweep variables in the Parametric Sweep Settings dialog. The topmost sweep variable in the list will form the outermost nested loop, and the sweep variable at the bottom of the list will form the innermost nested loop. You can change the order of the sweep variables using the Move Up and Move Down buttons of this dialog.
At the end of a multivariable sweep simulation, the output data files contain as many columns as the number of the sweep variables on the left holding the individual sweep variable sample values plus the last column(s) holding the standard or custom output parameters. The order of the sweep variable columns from left to right is identical to the order of the sweep variables in the Parametric Sweep Settings dialog.
Conducting Dry Runs
The Parametric Sweep Settings dialog also features another useful button labeled Dry Run, which runs a "fake" sweep animation. During a dry run, the sweep variables are varied sample by sample and all of their associated parameters in the project workspace are updated at each run. However, no simulation engine is called during a dry run, and no simulation data are generated. Also, the Variable Dry Run dialog appears on the screen which shows the changing values of all the variables at all times. The dry run process continues indefinitely until you stop it by clicking the close (X) button of the Dry Run dialog of simply hitting the keyboard's Esc key.
Running Monte Carlo Simulations in EM.Cube
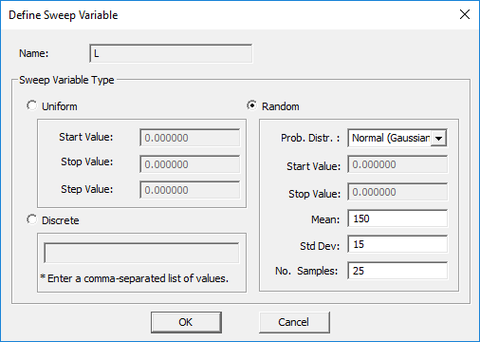
Specifying the Random Variables
EM.Cube allows you to define sweep variables of random type. When you designate an independent variable as a sweep variable, you can choose the "random variable" option of the "Define Sweep Variable" dialog. The currently available statistical distribution types are Uniform and Normal Gaussian. In the case of uniform distribution, you need to specify the lower and upper bounds of the random variable and the total number of samples. The samples of the random variable are picked randomly between the start and stop values. In the case of normal Gaussian distribution, you need to specify the samples' mean and standard deviation along with the total number of samples.
Post-Processing the Output Simulation Data
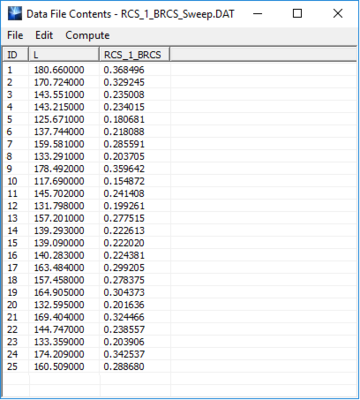
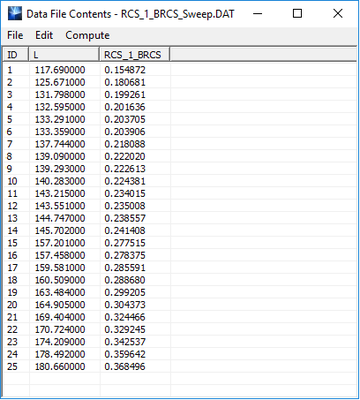
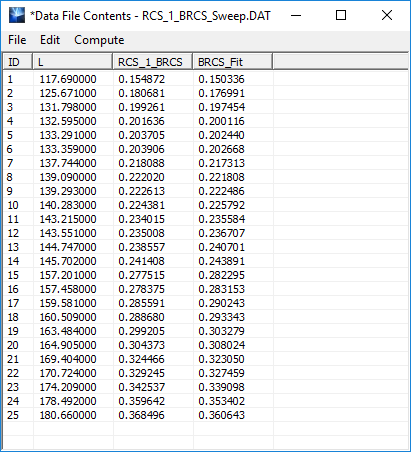
Similar to the other parametric sweep types, at the end of a Monte Carlo simulation, the output simulation data are stored and written to ASCII data files of various types with ".DAT", ".CPX" or ".ANG" file extensions. Since the sweep variable samples are randomly generated in this case, they are not ordered in ascending order. Before plotting the data in EM.Grid, you may have to order the sweep variable column. You can do this easily by opening the data file in Data Manager's spreadsheet and clicking on the title of the variable column at the top of the spreadsheet. In the example below showing the output data file for the back-scatter RCS at the end of a Monte Carlo simulation, you simply click on the "L" column header to sort the spreadsheet.
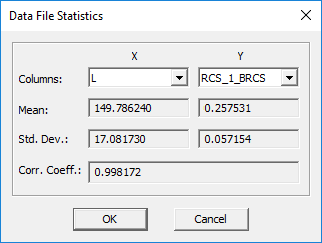
You can compute the statistical characteristics of your Monte Carlo simulation data using the "Compute" utilities of Data Manager's spreadsheet. While a sweep data file is open in the spreadsheet, select the menu item Compute → Statistics.... The "Data File Statistics" dialog opens up. In this dialog, you can see the mean and standard deviation of the X and Y column data (σX, σY) as well as their (Pearson) correlation coefficient defined as:
- [math]\rho = \frac {\operatorname{cov}(X,Y)} { \sigma_X \sigma_Y }[/math]
where the covariance between X and Y is defined as:
- [math]\operatorname{cov} (X,Y)=\frac{1}{N}\sum_{i=1}^N (x_i-E(X))(y_i-E(Y)) [/math]
In the case of several random sweep variable, the correlation coefficient between the variables pairs can be measured in this way.
After sorting the output simulation data, you can fit them using the least squares method. For this purpose, select the menu item Compute → Least Squares Fit.... The "Least Squares Fit" dialog opens up. In this dialog, you need to specify the independent (X) and dependent (Y) variable columns and choose a name for the new column to be generated, which will contain the fitted data for the same values of the X variable.
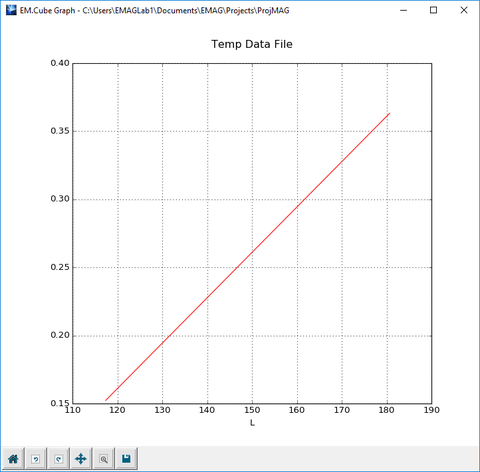
From the Data Manager's spreadsheet utility, you can also plot one column versus another column. To do so, select the menu item Plot → Cartesian to open the "Data File Plot" dialog. Here, too, you need to specify the independent (X) and dependent (Y) variable columns. Click the Plot button of this dialog to graph the data with PyPlot.
Generating Surrogate Models
In many practical situations, you may deal with highly complex modeling problems that involve a large and diverse set of parameters. Most of these parameters are oftentimes either fixed or have limited ranges or take on a few discrete values. Therefore, the variation of only a limited number of parameters might be of interest to you. As a simple example, consider a patch antenna with a single-layer conductor-backed dielectric substrate. The substrate parameters include the thickness h, relative permittivity εr and possibly tangent loss tanδ if losses are not negligible. It is one thing to develop a macromodel for the input impedance or radiation pattern of a patch antenna as a general function of h, εr and tanδ for all possible values of these variables. It would be an entirely different matter if you are just interested in practical substrates, which printed circuit board suppliers offer in a few thickness and material varieties.
EM.Cube allows you to develop computationally efficient and compact models of complex processes as functions of several parameters. This process is based on the High-Dimensional Model Reduction (HDMR) method. In the HDMR method, you run successive evaluations of a given function of one or more variables for a number of variables samples. Then you create an optimal monomial-based surface representation of the computed data as a function of those variables. The resulting simplified function is characterized by a finite number of monomial coefficients that are stored in an ASCI data file with a ".HDM" file extension. Obviously, the computation of the reduced surrogate function is much more faster and computationally more efficient than the original function used to create the source data. In the context of EM.Cube, the original function is indeed represented by a parametric sweep simulation that generated one or more output quantities of interest for each combination of the input input variable values.
Defining the HDMR Variables
To define the HDMR variables, follow the procedure below:
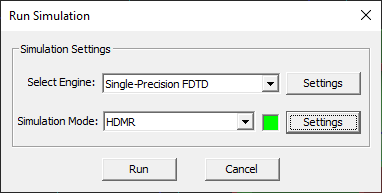
- Open the Simulation Run Dialog of most of EM.Cube's computational modules and select the HDMR option from the Simulation Mode dropdown list.
- Click the Settings button next to the simulation mode dropdown list to open up the HDMR Settings Dialog.
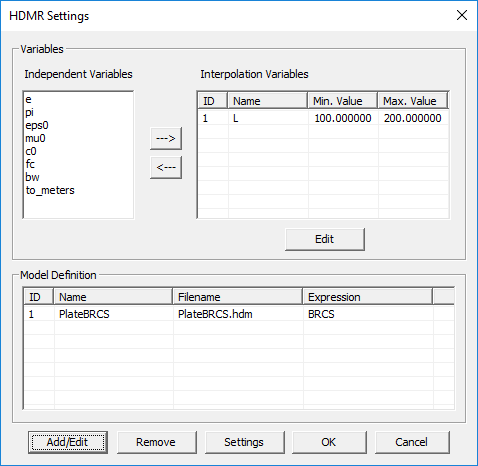
- On the left side of the "Variables" section of the dialog you see the "'Independent Variables Table", which lists all the available independent variables of your project. Select an independent variable from the table and use the Right Arrow --> button of the dialog to move it to the "HDMR Variables Table".
- Before moving the variable to the new location, the "Define Optimization Variable " dialog opens up, where you have to define the start and stop values of the variable (ignore the precision).
- Once you finish the definition of an HDMR variable, its name and attributes are added to the HDMR variables list.
Note that you can change your mind and remove an HDMR variable from the list. To do so, select its name or row from the list and use the Left Arrow <-- button to move it back to the independent variables table. You can also change the attribute values of an HDMR variable after it has been defined. Select the variable from the list and click the Edit button of the dialog.
Defining the HDMR Models
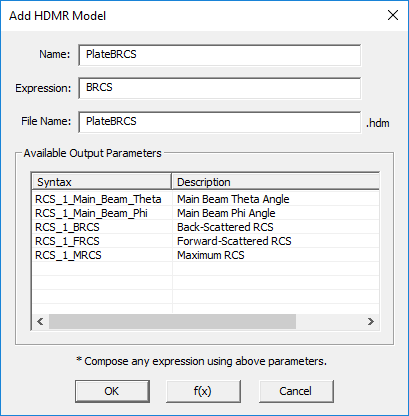
To define an HDMR model, follow the procedure below:
- Click the Add/Edit button in the "Model Definition" section of the HDMR Settings dialog to open up the Add HDMR Model Dialog.
- Choose a name for your HDMR model. Make sure that this name is unique and does not conflict with the existing data file names in your project's folder. Also make sure that your chosen name isn't one of the standard, preloaded or user-defined Python functions.
- At the bottom of the "Add HDMR Model" dialog, you will see a list of all the available EM.Cube standard output parameters. This list may vary depending on the types of sources and observables you have defined in your project.
- Type in any mathematical expressions in the box labeled Expression. If you select the name of any standard parameter in the table and double-click on it, it will be reflected in the expression box. Your expression can involve elementary and advanced mathematical functions as well as standard, preloaded or user-defined Python functions or the names of your project's variables.
- You can have different names for your HDMR model and its model file with the .HDM file extension. But it is recommended that you choose the same name.
Select one of the available options in the dropdown list labeled Logical Operator. The default operator is "== (Equal To)".
- Once the definition of your HDMR model is complete, click the OK button of the dialog to close it and return to the HDMR Settings dialog.
- You will see your new HDMR model added to the model list table.
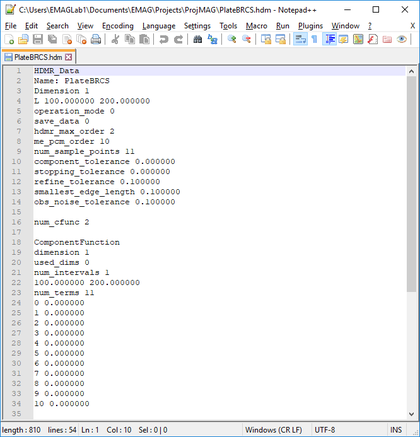
You can modify a model definition using the Add/Edit button of the HDMR settings dialog. You can also define more than one HDMR model at a time. Such models will be generated using the same simulation runs. However, it is recommended not to generate unrelated models together. In the example below, we have defined an HDMR model called "PlateBRCS" for the back-scatter RCS of a square metal plate as a function of its side dimension defined by an independent variable "L".
Running an HDMR Sweep
After you define all of your HDMR variables and model(s), close the HDMR Settings dialog to return to the simulation Run dialog. When you click the Run button of the Simulation Run dialog to start the HDMR sweep process, an Output Window pops up that reports the various stages of the sweep loop and displays the progress or percentage of completion. After the sweep process is finished, an HDMR file with a .HDM file extension is added to the "Models" sub-folder under "Documents → EMAG", which contains all the monomial coefficients of your HDMR model.
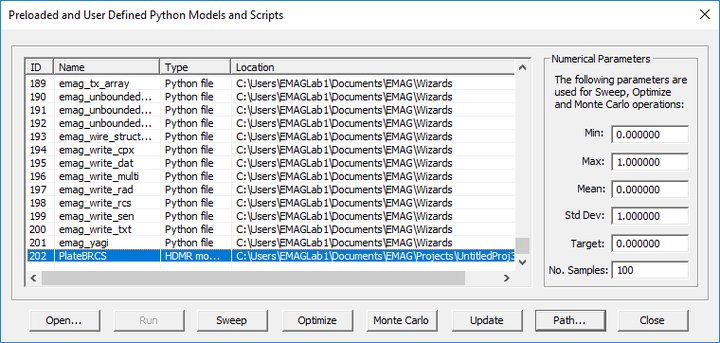
Note that once you generate an HDMR model, you can use it everywhere in EM.Cube just like any standard or library function. In the above example, the syntax of your new custom function is PlateBRCS(L) or PlateBRCS(x). All of you generated HDMR models are listed in EM.Cube's models dialog. You can access this dialog by clicking the Models ![]() button of the Simulate Toolbar or selecting the menu item Simulate → Models... or using the keyboard shortcut Ctrl+L. In the models dialog's list, select and highlight any model and click the Open button of this dialog to open the contents of the selected model file in your text editor of choice.
button of the Simulate Toolbar or selecting the menu item Simulate → Models... or using the keyboard shortcut Ctrl+L. In the models dialog's list, select and highlight any model and click the Open button of this dialog to open the contents of the selected model file in your text editor of choice.
Performing Optimization in EM.Cube
Planning for Optimization
Optimization is the process of finding the values of one or more variables that minimize a given error function. The error function, also known as the objective function, is typically a mathematical expression involving the optimization variables, functions of these variables and other fixed or variable quantities. You can perform optimization simulations in most of EM.Cube's computational modules. A simulation engine, in effect, can be regarded as a virtual function that takes a number of arguments defined by your project variables as input values, and then returns a number of standard or custom output parameters as output values. You can build your error or objective function based on these output parameters. You can also run optimizations of the surrogate models you create in EM.Cube.
Running an optimization process in EM.Cube involves a number of steps as follows:
- Defining the relevant design variables to be optimized
- Setting up the constraints, if any
- Defining the design objective(s)
- Constructing the error function based on the objectives and assigning weights
- Selecting the optimizer algorithm
- Running the simulation and waiting for the optimizer to converge
Each of these steps are described below in detail.
Understanding the Design Objectives
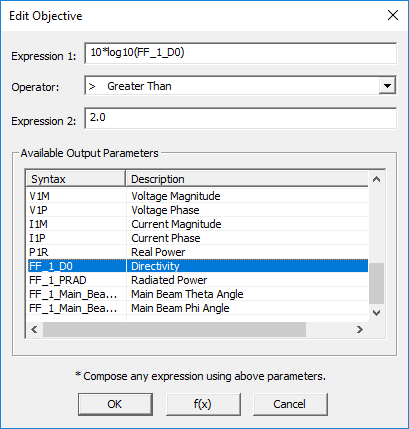
You can define a variety of design objectives in EM.Cube such as matching a one-port network and reducing its return loss to zero, or setting the insertion loss of a two-port network equal to a certain value, or tuning a radiator and setting its input reactance equal to zero, or obtaining a certain value of directivity from an antenna or array, or obtaining a certain value of RCS from a target, to name a few.
Design objectives are defined based on EM.Cube's standard or custom output parameters. These depend on what observables you have defined in your project. For example, if you have an antenna structure with a port definition, then you will have S11, Z11, Y11 and VSWR available for defining your objective. If your project's structure involves more than one port, then you also have all the Sij, Zij and Yij parameters. If you have defined a far-field observable, then the available output parameters include directivity (D0), total radiated power (PRAD), half power beam width (HPBW), maximum side lobe level (SLL), axial ratio (AR), etc. In periodic structures excited by a plane wave source, you also have access to the reflection coefficient (RC) and transmission coefficient (TC).
You can define more than one design objective for your optimization process. You can give different weights to different design objectives based on their priority in your design.
![]() Click here to learn more about EM.Cube's Standard Output Parameters.
Click here to learn more about EM.Cube's Standard Output Parameters.
![]() Click here to learn more about Defining Custom Output Parameters.
Click here to learn more about Defining Custom Output Parameters.
Defining Design Objectives
A design objective in EM.Cube is a logical expression that relates two quantities with a relational operator. Most design objectives consist of a mathematical expression involving standard output parameters set equal to a constant target value. The target value on the right side of the logical expression can also be another mathematical expression. The available relational operators are: == (equal to), != (not equal to), < (less than), ≤ (less than or equal to), > (greater than), and ≥ (greater than or equal to).
To define a design objective, follow the procedure below:
- Open the Objectives Dialog either by clicking the Objectives
 button of the Simulate Toolbar, or by selecting the menu item Simulate → Objectives..., or using the keyboard shortcut Ctrl+J. The objectives dialog is initially empty.
button of the Simulate Toolbar, or by selecting the menu item Simulate → Objectives..., or using the keyboard shortcut Ctrl+J. The objectives dialog is initially empty.
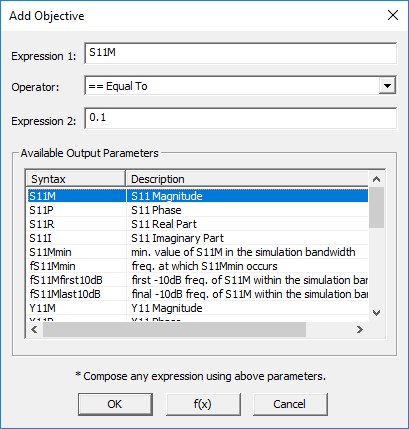
- To add a new objective, click the Add button of the dialog to open up the Add Objective Dialog. At the bottom of this dialog, you can see a list of all the available EM.Cube standard output parameters. This list may vary depending on the types of sources and observables you have defined in your project.
- Type in any mathematical expressions in the boxes labeled Expression 1 and Expression 2. If you select the name of any standard parameter in the table and double-click on it, it will be reflected in the expression box that has the mouse focus.
- Select one of the available options in the drop-down list labeled Logical Operator. The default operator is "== (Equal To)".
- Once the construction of your objective is complete, click the OK button on the dialog to close it and return to the Objectives dialog.
You will see your new objective added to the Objective List table. You can modify a design objective using the Edit button of the objectives dialog. Only design objectives that contain the logical operator "==" can be used as an optimization goal. All the design objectives that contain a logical operator other than "==" are treated as optimization constraints. This means that the optimizer algorithm first tries to minimize an error function that is based on the goals solely and then it verifies whether the constraints are satisfied additionally.
![]() Click here to learn more about Python's Standard & Advanced Mathematical Functions.
Click here to learn more about Python's Standard & Advanced Mathematical Functions.
![]() Click here to learn more about Creating Custom Python Functions.
Click here to learn more about Creating Custom Python Functions.
EM.Cube's Optimization Algorithms
EM.Cube offers three different types of optimization algorithms:
- Powell's method of Conjugate Directions
- A Basic Evolutionary Genetic Algorithm (GA)
- A Fast Multi-Objective Pareto Algorithm
Powell's method is a classical optimizer based on the method of conjugate directions, which is similar to the conjugate gradient (CG) method but it avoids direct calculation of the derivatives. If your project has N optimization variables, then an N-dimensional vector space is constructed. The algorithm searches for the minimum along linear directions in the N-dimensional space. A weakness of Powell's method is that it may get trapped at local minima.
EM.Cube's evolutionary genetic algorithm constructs continuous chromosomes from the vector of optimization variables. Then, it creates populations with different chromosomes using evolutionary operations such as uniform and non-uniform mutation, arithmetic and heuristic crossover and recombination. At each generation, the best-fit solutions are selected and their genes are passed to the next generation. Since very large populations may be developed during this process, genetic algorithms can be exhaustive and computationally very expensive. However, a major advantage of genetic algorithm is that they find the global minimum and do not get trapped around local minima. Pareto algorithm is an advanced evolutionary genetic algorithm that is particularly efficient when the optimization is trying to achieve a large number of simultaneous design objectives.
![]() For a theoretical discussion of the Pareto optimization algorithm, see Multi-Objective Optimization on Wikipedia.
For a theoretical discussion of the Pareto optimization algorithm, see Multi-Objective Optimization on Wikipedia.
Defining the Optimization Variables & Other Settings
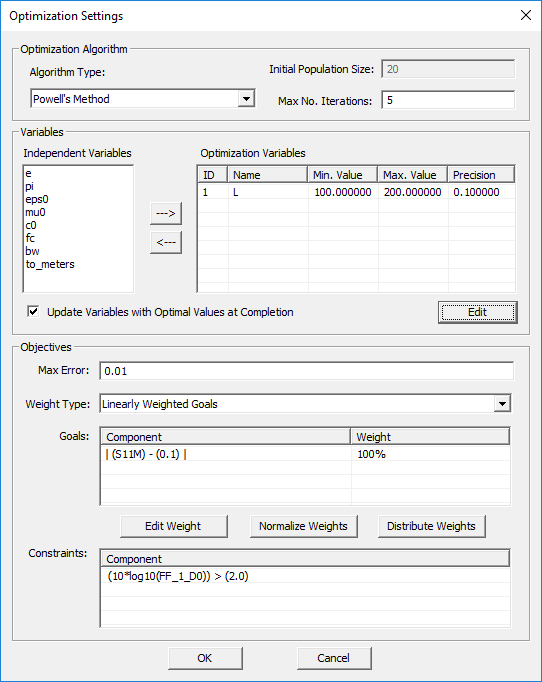
Most of the optimization parameter are define using EM.Cube's Optimization Settings dialog. To access this dialog, follow the procedure below:
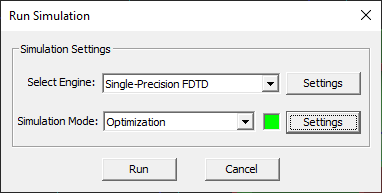
- Open the Simulation Run dialog of any of EM.Cube's computational modules and select the Optimization option from the Simulation Mode drop-down list.
- Press the Settings button next to the simulation mode drop-down list to open up the Optimization Settings Dialog.
- At the top section of this dialog, you can select the Optimizer Algorithm, which offers three options: Powell' Method, Basic Genetic Algorithm and Fast Pareto Algorithm.
- In the case of the two genetic algorithms, you can set the Initial Population Size, which has a default value of 20. The actual population size is indeed this number multiplied by 5, as five evolutionary operations are performed on the chromosomes.
- You can also set the Maximum Number of Iterations, which has a default value of 5.
You have to select your optimization variables from the list of your project's independent variables just as you do for sweep variables in a parametric sweep. Keep in mind that you cannot designate a dependent variable as an optimization variable because you cannot vary its value directly. Dependent variables can be used to tie up different object parameters in quite complicated ways. This is part of the planning process for optimization. The more constraints you define for your object properties, the fewer independent variables you will have to vary during optimization.
| |
Optimization simulations, particularly those involving full-wave simulation engines, can be extremely time consuming. |
To designate an independent variable as an optimization variable, follow the steps below:
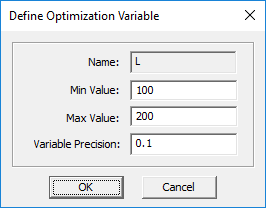
- Select one of the entries in the Independent Variables list box on the left side of the "Variables" section of the dialog and move it to the Optimization Variables list box on the right side by clicking the Right Arrow ---> button.
- A new dialog titled Define Optimization Variable opens up, where you can specify the optimization variable's range and its precision. The variable's precision is the minimum value by which it can be changed by the optimization algorithm.
- Click OK button after specifying the optimization variable's minimum value, maximum value and precision to return to the Optimization Settings dialog.
You can change the attributes of an optimization variable using the Edit button of the Optimization Settings dialog. You can also remove any optimization variable from the list box on the right by selecting it and using the Left Arrow <--- button to move it back to the independent variables list box on the left.
Running a Single-Objective Optimization Simulation
Only the design objectives that involve the "Equal To (==)" logical operator are used for the construction of the error function. If your project has only one design objective of the form "Expression 1 == Expression 2", then the error function is simply defined as "Error = | Expression 1 - Expression 2 |". In most cases, "Expression 2" is simply a fixed target value. For example, the objective "S11M == 0.1" leads to an error function of the form | S11M - 0.1 | as you can see in the above figure. In the Optimization Settings dialog, you can also set the value of Max Error, which has a default value of 0.01. When the computed value of the error function falls below this tolerance, the optimization process is considered to have converged and it is terminated. Otherwise, the optimization loop continues until it reaches the specified Maximum Number of Iterations.
When you click the Run button of the simulation run dialog to start the optimization process, an Output Window pops up that reports the various stages of the optimization loop and displays the progress or percentage of completion. At every run, you can see the new values of the optimization variables as well as the computed error. After the optimization converges, all the optimization variables are updated with their optimal values by default. You can disable this feature by unchecking the box labeled Update Variables with Optimal Values at Completion.
In some cases, the optimizer algorithm may get trapped around a local minimum. The consecutive values of the optimization variable get closer and closer to a "fake solution" as if the process is converging. If the successive values of the optimization variable stay the same within the specified precision while the value of the error function is still larger than your specified maximum error, it is considered as a local minimum trap and the optimization process is terminated.
Building the Error Function for a Multivariable Optimization
EM.Cube allows you to define more than one design objective. If you have NOBJ goals or objectives with the "Equal To (==)" logical operator, then error components are built from each design objective:
ek = | (Expression 1)k - (Expression 2)k |, k = 1, 2, ..., NOBJ.
You can assign different weights to these error components. By default, all the weights are zeros. In other words, the error function is initially not constructed. It is your responsibility to build it. In the "Objectives" section of the Optimization Settings dialog, you will see a list of all the defined goals as well as a list of all the constraints (non-goal objectives). If you click the Distribute Weights button of the dialog, the weights are distributed equally among all the goals. You can also manually edit the weight values and use the Normalize Weights button of the dialog to adjust them properly.
| |
You can assign a zero weight to a goal to effectively remove it from the objective function. |
EM.Cube gives you two options to apply the weights in the construction of the project's error function. The drop-down list labeled Weight Type gives two options:
- Linearly Weighted Goals: Error = Σ( wk . ek)
- Mean Square Weighted Goals: Error = sqrt( Σ( wk . | ek |2 ) )
where wk denotes the weights.