Defining Project Observables & Visualizing Output Data
Contents
- 1 The Objective of a Numerical Simulation
- 2 The Variety of Simulation Data and Observable Types in EM.Cube
- 3 An Overview of EM.Cube Data Types
- 4 Basic 2D Data Files
- 5 Basic 3D Data Files
- 6 The Data Manager
- 7 EM.Cube's Basic Graph Types
- 8 The PyPlot Window
- 9 Customizing a Graph
- 10 Using Data Manager's Spreadsheet
- 11 Data Manager's Computational Tools
- 12 Graphing Port Characteristics & Other Complex-Valued Data
- 13 Rational Interpolation of Port Characteristics
- 14 Probing Fields in Time and Frequency Domains
- 15 Visualizing & Plotting Near-Field Distributions
- 16 Plotting Field Distribution Graphs Along Lines
- 17 Visualizing & Plotting Current Distributions
- 18 Visualizing & Plotting Far-Field Radiation Patterns
- 19 Using Array Factor to Model Antenna Arrays
- 20 Far Field Data Files
- 21 Visualizing & Plotting Radar Cross Section
- 22 3D Field Animation
- 23 Building New Data Files from Scratch
- 24 Using Data Manager to Create New Data Files
- 25 Using Spatial Data Generator to Create New 3D Data
- 26 Visualizing 3D Data in CubeCAD
The Objective of a Numerical Simulation
Each of EM.Cube's computational modules provide one or more electromagnetic field solvers. At the end of a simulation, either the electric and/or magnetic fields in the computational domain are determined directly, or the electric and/or magnetic currents are computed, from which one can also determine the electric and magnetic fields. Electric and magnetic fields and currents are considered "primary" solutions or output quantities. In many practical cases, you may not be directly interested in the field or current distributions. Rather, you may want to compute "secondary" quantities such as input impedance, return loss, radiation pattern, radar cross section, or reflection and transmission coefficients of a periodic structure. These quantities are computed at the post-processing stage of a numerical simulation. Because the calculation of many of these characteristics are often time consuming, the data are not generated automatically. In most of EM.Cube's computational modules, you have to define one or more observables to generate any output data at the end of a simulation. In other words, no simulation data is generated until you instruct EM.Cube to do so. EM.Cube provides a large variety of simulation data and observable types. Most of the output simulation data types are saved in ASCII data files. These data can be plotted or loaded into Python arrays for further processing.
![]() Click here to access Glossary of EM.Cube's Simulation Observables & Graph Types.
Click here to access Glossary of EM.Cube's Simulation Observables & Graph Types.
The Variety of Simulation Data and Observable Types in EM.Cube
EM.Cube provides a large variety of simulation data and observable types as listed in the table below:
| Simulation Data Type | Required Observable | Supporting Module(s) |
|---|---|---|
| Electric and Magnetic Field Distributions | Field Sensor | EM.Tempo, EM.Terrano, EM.Ferma, EM.Picasso, EM.Libera, EM.Illumina |
| Electric and Magnetic Current Distributions | Current Distribution | EM.Picasso, EM.Libera, EM.Illumina |
| Temporal Fields | Field Probe | EM.Tempo |
| Far-Field Radiation Patterns | Far-Field Radiation Pattern | EM.Tempo, EM.Picasso, EM.Libera, EM.Illumina, EM.Terrano |
| Radiation Characteristics (D0, HPBW, SLL, AR, etc.) | Far-Field Radiation Pattern | EM.Tempo, EM.Picasso, EM.Libera, EM.Illumina, EM.Terrano |
| Radar Cross Section (RCS) | RCS | EM.Tempo, EM.Picasso, EM.Libera, EM.Illumina |
| Equivalent Electric and Magnetic Surface Current Data | Huygens Surface | EM.Tempo, EM.Picasso, EM.Libera, EM.Illumina, EM.Terrano |
| Port Characteristics (S/Z/Y Parameters) | Port Definition | EM.Tempo, EM.Picasso, EM.Libera |
| Port Voltags, Currents & Powers | Port Definition | EM.Tempo |
| Periodic Reflection and Transmission Coefficients | No Observables Required | EM.Tempo, EM.Picasso |
| Temporal Electric and Magnetic Energies and Dissipated Power | Energy-Power | EM.Tempo |
| Electric and Magnetic Energy Densities and Dissipated Power Density | Field Sensor & Energy-Power | EM.Tempo, EM.Ferma |
| Specific Absorption Rate (SAR) Density | Field Sensor & Energy-Power | EM.Tempo |
| Complex Poynting Vector | Field Sensor & Energy-Power | EM.Tempo |
| Static Electric and Magnetic Energies & Ohmic Losses | Field Integral | EM.Ferma |
| Voltage and Current | Field Integral | EM.Ferma |
| Electric and Magnetic Flux | Field Integral | EM.Ferma |
| Resistance, Capacitance, Self-Inductance and Mutual Inductance | Field Integral | EM.Ferma |
| Temperature and heat flux distributions | Field Sensor | EM.Ferma |
| Thermal energy density | Field Sensor | EM.Ferma |
| Thermal Flux and Thermal Energy | Field Integral | EM.Ferma |
| Received Power | Point Receiver Set | EM.Terrano |
| Channel Path Loss | Point Receiver Set | EM.Terrano |
| Singal-to-Noise Ratio (SNR) | Point Receiver Set | EM.Terrano |
| Eb/N0 | Point Receiver Set | EM.Terrano |
| Bit Error Rate (BER) | Point Receiver Set | EM.Terrano |
| Power Delay Profile | Point Receiver Set | EM.Terrano |
| Angles of Arrival and Departure | Point Receiver Set | EM.Terrano |
An Overview of EM.Cube Data Types
EM.Cube's various computational modules and simulation engines generate a large variety of data representing field values, current distributions, port characteristics like S/Z/Y parameters, radiation patterns, radar cross sections, reflection and transmission coefficients, capacitance, inductance, etc. Some of these data are real-valued, and some are complex-valued. Some represent scalar physical quantities, while others represent vector quantities. For example, the static electric and magnetic fields in EM.Ferma or the time domain fields in EM.Tempo are real-valued vectors, while the frequency domain field quantities in EM.Picasso, EM.Libera and EM.Illumina are complex-valued vectors. The electric potential in EM.Ferma is a real-valued scalar quantity. Scattering (S), impedance (Z) and admittance (Y) parameters as well as reflection (R) and transmission (T) coefficients of periodic surfaces are all complex-valued scalar quantities often expressed as functions of frequency. Some data such as field and current distributions are also spatial by nature, meaning they are defined on a set of points in the 3D space, possibly on a plane or on a surface mesh.
In the most general sense, one can think of four data types:
- Real scalar
- Complex scalar
- Real vector
- Complex vector
Most of EM.Cube's simulation data are written to ASCII data files. The data values are arranged in columns in an ASCII data file. For example, the data file containing the voltage standing wave ratio (VSWR) has two columns. The firs column contains the frequency values and the second column contains the real-valued VSWR. A complex scalar quantity is represented by two columns, one for the real part and the other for the imaginary part. A real vector quantity is represented by three columns for the three X, Y and Z components. A complex vector quantity is represented by six columns, two for each component's real and imaginary parts.
Basic 2D Data Files
2D numeric data files contain data that can be plotted on 2D graphs. In general, EM.Cube supports four such data file types:
- Real Data
- Complex Data
- Angular Data
Real data represent one or more sets of real numbers (dependent variables) as functions of one or more real variables (independent variables). Real data must be saved to a file with a .DAT extension such as "MyRealData.dat". Examples of real data are voltage standing wave ratio (VSWR) vs. frequency, directivity of a dipole antenna vs. its length or path loss of a receiver set vs. the receiver index.
Complex data represent one or more sets of complex numbers (dependent variables) as functions of one or more real variables (independent variables). Complex data must be saved to a file with a .CPX extension such as "MyComplexData.cpx".Examples of complex data are the scattering, impedance or admittance parameters of a two-port network.
Angular data represent one or more sets of real numbers (dependent variables) as functions of an angle expressed in degrees. Angular data must be saved to a file with a .ANG extension such as "MyAngularData.ang". Examples of angular data are 2D polar radiation patterns of an antenna or 2D polar radar cross section (RCS) of a target in the principal planes vs. the elevation or azimuth angles.
EM.Cube's computational modules generate a large number of 2D data files, some of which are listed below:
| 2D File Name | File Extension | Purpose | 2D Data Type |
|---|---|---|---|
| Sij | .CPX | scattering parameters | complex |
| Zij | .CPX | impedance parameters | complex |
| Yij | .CPX | admittance parameters | complex |
| VSWR | .DAT | voltage standing wave ratio | real |
| reflection_coefficient | .CPX | reflection coefficient of periodic surfaces | complex |
| transmission_coefficient | .CPX | transmission coefficient of periodic surfaces | complex |
| FF_1_PATTERN_CART_YZ | .DAT | 2D Cartesian radiation pattern in YZ plane | real |
| FF_1_PATTERN_POLAR_YZ | .ANG | 2D polar radiation pattern in YZ plane | angular |
| FF_1_RCS_CART_YZ | .DAT | 2D Cartesian radar cross section in YZ plane | real |
| FF_1_RCS_POLAR_YZ | .ANG | 2D polar radar cross section in YZ plane | angular |
| ProbeName_X_E_Time | .DAT | variation of the electric field component vs. time | real |
| ProbeName_X_E_Fre | .CPX | variation of the electric field component vs. frequency | complex |
| Sensor_1_X_ETotal | .DAT | total electric field distribution along X direction | real |
| Sensor_1_X_HTotal | .DAT | total magnetic field distribution along X direction | real |
| D0 | .DAT | directivity | real |
| voltage | .DAT | voltage along the specified path | real |
| current | .DAT | total current passing through the specified loop | real |
Basic 3D Data Files
3D numeric data files contain data that require 3D visualization. Such data are expressed at functions of space coordinates either in the Cartesian or spherical coordinated system. Most of EM.Cube's 3D data files are vectorial in nature. In general, EM.Cube supports three 3D data file types:
- Cartesian Data
- Spherical Data
- Mesh Data
Cartesian data represent one or more sets of real or complex numbers (dependent variables) as functions of 3D point coordinates (X, Y, Z). In most general case, they represent values of scalar or vector functions at the points inside a given cubic grid. If one of the three coordinates is fixed, then the domain will represent the points on a grid plane. Cartesian data are saved to a file with a .CAR extension such as "MyVolumeData.car". Examples of Cartesian data are the electric or magnetic field distributions on field sensor planes or the electric scalar potential or magnetic vector potential.
Spherical data represent one or more sets of real or complex numbers (dependent variables) as functions of the two spherical angles θ and φ expressed in radians. In other words, they represent the values of scalar or vector functions on a unit sphere. Spherical data are saved to a file with a .SPH extension such as "MySphericalData.sph". Examples of spherical data are 3D far-field radiation patterns of antennas or 3D radar cross section (RCS) of targets.
Mesh data represent one or more sets of real or complex numbers (dependent variables) as functions of 3D point coordinates over a surface mesh. The data values are indeed defined at the centroid of each mesh cell. The mesh cells can be triangular, rectangular or even linear like in a wireframe mesh. Mesh data are saved to a file with a .MSH extension such as "MySurfaceData.msh". Examples of mesh data are electric and magnetic surface current distributions.
Besides the generalized 3D data types discussed above, EM.Cube's computational modules generate a number of specialized 3D data files as follows:
| 3D File Type | File Extension | Purpose | 3D Data Type |
|---|---|---|---|
| Near-Field Distribution Data File | .SEN | Electric and magnetic field distributions | Cartesian |
| Current Distribution Data File | .CUR | Electric and magnetic surface current distributions | Mesh |
| Far-Field Radiation Pattern Data File | .RAD | 3D radiation patterns | Spherical |
| RCS Data File | .RCS | 3D radar cross section | Spherical |
| Directive Gain Data File | .SPH | 3D directive gain pattern | Spherical |
| Axial Ratio Data File | .SPH | 3D axial ratio pattern | Spherical |
| Coverage Data File | .COV | Received power coverage map | Cartesian |
| Huygens Surface Data File | .HUY | Equivalent Huygens electric and magnetic surface currents | Cartesian |
The Data Manager
EM.Cube allows you to view data files, modify their contents, perform data operations and calculations, and plot graphs or render 3D visualizations of the data. EM.Cube's computational modules generate a variety of input and output data files, all of which have similar standard formats. You can also bring in external data (e.g. measurement data) and cast them into an appropriate file format. You can access all of these data files from EM.Cube's Data Manager.
| |
All of EM.Cube's computational modules share the same data visualization and processing utilities. |
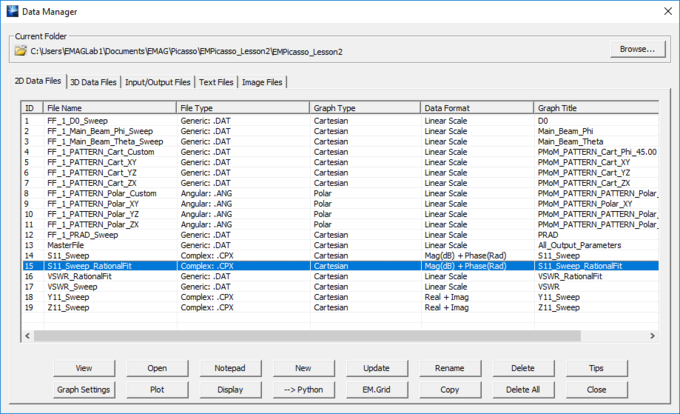
To access data files and view or graph them in EM.Cube, first open the "Data Manager" by clicking the Data Manager ![]() button of the Simulate Toolbar or selecting the menu item Simulate → Data Manager or right-clicking on the Data Manager item of the navigation tree and selecting Open Data Manager... from the contextual menu or simply using the keyboard shortcut Ctrl+D. By default, Data Manager opens at the current project folder. The path of the current directory is displayed at the top of the Data Manager dialog. Click the Browse... button of the dialog to open the Windows Explorer. Browse all the folders on your hard drive or on your network and select the desired folder to view its data files.
button of the Simulate Toolbar or selecting the menu item Simulate → Data Manager or right-clicking on the Data Manager item of the navigation tree and selecting Open Data Manager... from the contextual menu or simply using the keyboard shortcut Ctrl+D. By default, Data Manager opens at the current project folder. The path of the current directory is displayed at the top of the Data Manager dialog. Click the Browse... button of the dialog to open the Windows Explorer. Browse all the folders on your hard drive or on your network and select the desired folder to view its data files.
The data files are organized into five separate tabs:
- 2D Data Files
- 3D Data Files
- Input/Output Files
- Text Files
- Image Files
The following table shows the types of data files that are listed under each tab:
| Data Manager Tab | Listed Data File Types |
|---|---|
| 2D Data Files | .DAT, .CPX, .ANG, .SNP (.S1P, .S2P, etc.), .KBT |
| 3D Data Files | .CAR, .MSH, .SPH, .SEN, .CUR, .RAD, .RCS, .HUY, .COV |
| Input/Output Files | .IN, .OUT, .DAT1, .GRID, .MTL, .PEC, .PMC, .RTIN, .RTOUT, .BDG, .TRS, .RCV, .GRN, .CIR, etc. |
| Text Files | .TXT, .LOG |
| Image Files | .BMP, .PNG, .JPG, .GIF |
Data Manager has a number of buttons as follows:
| Button Name | Function | Tabs |
|---|---|---|
| View | Opens a spreadsheet view of the data file | 2D Files, 3D Files, Input/Output Files, Text Files, Image Files |
| Open | Opens the selected files in an application associated with the file extension | 2D Files, 3D Files, Input/Output Files, Text Files |
| Notepad | Opens the selected files in Windows Notepad application | 2D Files, 3D Files, Input/Output Files, Text Files |
| New | Creates a new data file from scratch | 2D Files, 3D Files |
| Delete | Deletes the selected files | 2D Files, 3D Files, Input/Output Files, Text Files, Image Files |
| Delete All | Deletes all the files in the current tab | 2D Files, 3D Files, Input/Output Files, Text Files, Image Files |
| Graph Settings | Opens the Graph Settings dialog for plot customization | 2D Files, 3D Files |
| Plot | Plots the contents of the selected files in PyPlot graphs | 2D Files, 3D Files |
| Display | Displays an image of a previously plotted graph in Windows Image Viewer | 2D Files, 3D Files |
| -->Python | Converts the contents of the selected data file to a Python NumPy array of the same name | 2D Files, 3D Files |
| Update | Updates the lists of all Data Manager tabs | 2D Files, 3D Files, Input/Output Files, Text Files, Image Files |
| Close | Closes the Data Manager dialog | 2D Files, 3D Files, Input/Output Files, Text Files, Image Files |
In each tab, click on the index, name or row of any data file to select and highlight it. You can select more than one data file at a time. Select a data file, and while holding the keyboard's Ctrl key down, select as many more data files as you want. All the selected data files will be highlighted. You can also select a range of data files from the list. Select the first data file, and while holding the keyboard's Shift key down, select the last data file from the list. All the data files in between will be highlighted, too.
EM.Cube's Basic Graph Types
EM.Cube provides a Python-based graphing utility that is used to plot a number of 2D and 3D graph types:
- Cartesian Graph
- Polar Graph
- Bar Graph
- Polar Stem Graph
- Smith Chart
- Colorgrid Plot
- Contour Plot
- Filled Contour Plot
- Surface Plot
Cartesian graphs are the simplest and most general type of graphs and can be used to plot real, complex and angular data. Any data file with a .DAT extension can be plotted as a Cartesian graph. When you select a data file in the Data Manager's 2D tab and click the Plot button, it plots the contents of the selected data file in a PyPlot window. PyPlot is a Python library for plotting and customizing graphs of datasets.
Polar graphs are used exclusively to plot angular data. The independent variable is represented by an angle (in degrees), while the dependent variable is represented by the radius from the origin of coordinates. A bar graph is a special type of a Cartesian graph where the data points are not connected with continuous lines. They are rather represented by vertical bars stemming from the horizontal axis. A polar stem graph is a special type of a polar graph where the data points are not connected with continuous lines. They are rather represented by radial bars stemming from the origin of coordinates. Smith charts are used exclusively to plot complex data such as S-parameters and periodic reflection coefficients. If the complex data are normalized (with a maximum unit magnitude), then the entire graph will be enclosed inside of the Smith chart.
Colorgrid, contour, filled contour and surface plot are used to visualize 3D spatial data of the form z = f(x,y). A data point on these plots represents the value of a dependent variable at a certain (X,Y) coordinate pair. Colorgrid plots use a color-coded intensity map. Contour and filled contour plots display the loci of constant z-values (isolines). Surface plots create a color-coded 3D surface over the data grid.
| |
If your 3D dataset contains a large number of data points, surface plots may take a very long time to appear t in a PyPlot window. Visualizing these kinds of data from EM.Cube's navigation tree is usually much faster. |
The PyPlot Window
When you plot a graph from Data Manager, a separate PyPlot window pops up that displays the plotted graph.
The PyPlot window has a number of controls you can use for customizing your graph. These are listed below:
There are also two keyboard shortcuts that can be used when a PyPlot window is open and active (in focus):
| Keyboard Shortcut | Function |
|---|---|
| Ctrl+W | Close the current PyPlot window |
| Ctrl+F | Toggle between full screen and original graph size |
| Ctrl+S | Save as Temp_Figure.PNG in Images folder |
| Home | Reset original view |
| p | Pan/Zoom |
| g | Toggle grid |
A PyPlot window is an active Python application that runs in the background while the window is open. As a result, you can only have one PyPlot window open at any time in each EM.Cube project. While a PyPlot window is open and possibly hidden under other windows, EM.Cube gives an error message if you try to plot another graph. You are prompted to first close the already open PyPlot window before proceeding to plot a new graph. It is important to know the difference between the two buttons Plot and Display. The former opens a PyPlot window and creates an interactive graph. The latter simply displays an image of a previously plotted graph in the Image Viewer. Note that while a PyPlot window is open, you can still display several graphs that were plotted previously.
You can select several data files from Data Manager and click the Plot button. In that case, graphs will be displayed sequentially one at time. In other words, you need to close each graph before you can view the next one in the selection list.
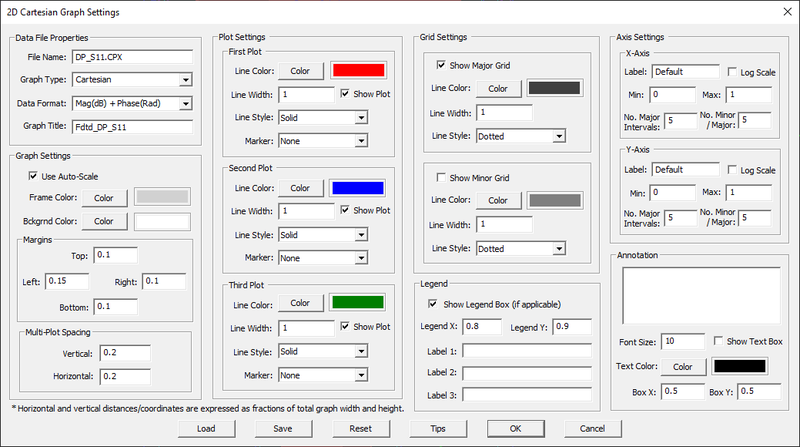
Customizing a Graph
EM.Cube provides a number of settings for each PyPlot graph. These are accessed using the Graph Settings dialog shown below:
Some data types and graph types can take different formats. For example, a real scalar data set can be expressed in linear or dB scales. Field quantities like voltage, S11, etc. are converted to dB scale as 20*log10(x), while power quantities like radiated power or directivity are converted to dB scale as 10*log10(x). Complex scalar data sets are typically plotted on double graphs and can be expressed as real and imaginary parts or as magnitude and phase. The magnitude of a complex quantity can be expressed in linear or dB scales. The phase can be expressed in radian or degrees. The table below summarizes some of these options for various data file types:
| Data File Type | Graph Type | Data Format | Python Script(s) |
|---|---|---|---|
| .DAT | Cartesian, Bar Chart | Linear Scale, dB_Field Scale, dB_Power Scale | emag_plot_dat.py, emag_plot_two_dat.py |
| .CPX | Double Cartesian, Smith Chart | Real + Imag, dB_Field + Phase(rad), dB_Power + Phase(Rad), Mag + Phase(Rad), dB_Field + Phase(Degrees), dB_Power + Phase(Degrees), Mag + Phase(Degrees) | emag_plot_cpx.py, emag_plot_two_cpx.py |
| .ANG | Polar, Polar Stem Chart | Linear Scale, dB_Field Scale, dB_Power Scale | emag_plot_ang.py, emag_plot_two_ang.py |
| .CAR | Colorgrid, Contour, Filled Contour, Surface | N/A | emag_plot_car_grid.py, emag_plot_car_contour.py, emag_plot_car_surf.py |
| .SEN | Double Colorgrid, Double Contour, Double Filled Contour, Double Surface | N/A | emag_plot_sen_grid.py, emag_plot_sen_contour.py, emag_plot_sen_surf.py, emag_plot_sen_tempo_grid.py, emag_plot_sen_tempo_contour.py, emag_plot_sen_tempo_surf.py, emag_plot_sen_ferma_grid.py, emag_plot_sen_ferma_contour.py, emag_plot_sen_ferma_surf.py |
| .COV | Colorgrid, Contour, Filled Contour | N/A | emag_plot_cov.py, emag_plot_cov_contour.py |
| .SPH | Spherical (3D Polar) | N/A | emag_plot_sph.py |
| .RAD | Spherical (3D Polar) | N/A | emag_plot_rad.py |
| .RCS | Spherical (3D Polar) | N/A | emag_plot_rcs.py |
The above table also shows the Python scripts used to plot each data file type. All of this scripts are stored in the "Documents/EMAG/Wizards".
Most of EM.Cube graphs are automatically scaled by PyPlot. You can override the default settings and customize various features of any graph. To do so, you may first need to uncheck the check box labeled Use Auto-Scale. For example, you can set the lower and upper limits (min and max values) of both horizontal and vertical axes. When both the min and max values of an axis are set equal to zero, that axis will be scaled automatically.
Using Data Manager's Spreadsheet
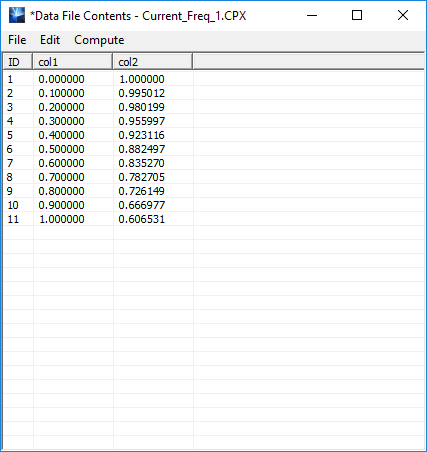
Although you can open any selected data file in Windows Notepad or any other text editor such as Notepad++, EM.Cube's Data Manager allows you to view the contents of a data file in a native spreadsheet. To open a data file in Data Manager's spreadsheet, select its name and click the View button of the dialog or simply double-click on its highlighted row. The data are organized in a tabular format featuring a number of indexed rows and titled columns. Rows are indexed as R1, R2, ... and columns have labels like col1, col2, ... The leftmost column (ID) shows the row index. You can adjust the width of columns manually using the mouse and dragging the borders of the column headers. But you cannot change the data values directly from the spreadsheet. To edit the values, you can open the spreadsheet's text editor by selecting the menu item Edit → Open Text Editor.
You can perform a number of operations on rows or columns of data. You can select and highlight an entire row by clicking on its index cell. To delete a selected row, select the menu item Edit → Remove Row(s). You can duplicate a selected row or add a new blank row. Column operations are slightly different. You can add one or more new blank columns. You can also duplicate, delete, rename or sort columns. To do so, select the proper menu item from the "Edit" menu. Each column-related menu item has a submenu that lists all the existing column names. If you click on the header of each column (where its name is displayed), it is sorted in the ascending order. Note that the entire spreadsheet has to be sorted as a result to preserve the rows. You can move and reshuffle the columns. To do so, simply grab the header of a column and drag it to the left or right and drop it in the desired place.
Data Manager's Computational Tools
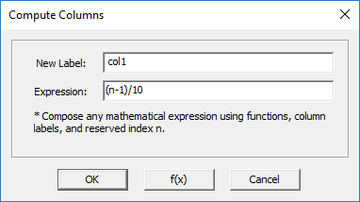
EM.Cube's Data Manager allows mathematical operations on both columns and rows. These tools can be accessed from the Compute Menu of the spreadsheet. For this purpose, the rows are denoted by R1, R2, ..., and the columns are represented by their actual header names. e.g. col1, col2, ... You can compose any mathematical expression or Python function involving the row names (R1, R2, etc.), columns names, project variables, Python global constants, as well as the reserved variable "n" which denotes the current row index in each column.
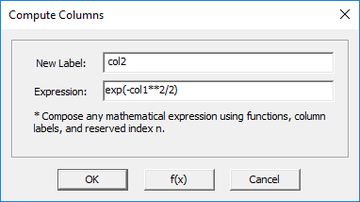
The "Compute Column" operation creates a new column or changes the contents of an existing column. The "Compute Row" operation creates a new row and adds it to the bottom of the spreadsheet. As an example, the figure below shows the Compute Columns dialog settings values for col1 and col2 of a spreadsheet. At the top, you enter the name of the column whose contents you want to change. If you type in a name that is not already a column header, a new columns by that name will be created and place as the rightmost column of the spreadsheet. In this example, we set col1 = n-1, and col2 = exp(-col1**2/2). Once you close the compute column dialog, the contents of column 1 are replaced with 0, 1, 2, ... In other words, each element in this column is replaced with its row index decremented by 1. The contents of Column 2 are then calculated based on the value of Column 1 using the specified expression. This operation is very similar to element-wise array operations in Python or Matlab.
The table below summarizes the tools and operations available under the Compute menu of Data Manager's spreadsheet:
| Tool | Function |
|---|---|
| Compute Columns | Performs general mathematical and/or Python operations on one or more columns and creates a new column for the results. |
| Compute Rows | Performs general mathematical and/or Python operations on one or more rows and creates a new column for the results. |
| Matrix Computations | Computes the minimum, maximum, norm, mean, standard deviation, sum and product of any subset of the entire spreadsheet regarded as a matrix and shows the results in the dialog. |
| Derivative | Computes the derivative of column Y with respect to column X and creates a new column for the results. |
| Integral | Computes the integral of column Y with respect to column X and shows the results in the dialog. |
| Discrete Fourier Transform | Computes the complex-valued DFT of a selected column and creates two new columns for the real and imaginary parts of the results. |
| Statistics | Computes the mean, standard deviation and correlation coefficient of any two selected columns and shows the results in the dialog. |
| Least Squares Fit | Computes the least squares fit (linear regression) of column Y with respect to column X and creates a new column for the fitted results. |
Graphing Port Characteristics & Other Complex-Valued Data
If your physical structure has a port definition observable, then the scattering [S], impedance [Z] and admittance [Y] parameters of your multiport network are computed at the end of an EM.Cube simulation. EM.Tempo, EM.Picasso and EM.Libera are three EM.Cube modules that allow for port definitions. Each port is excited separately with all the other ports turned off. When the jth port is excited, all the Sij parameters are calculated during a single engine run. At the end of the full-wave simulation, the S/Z/Y parameters are written into output ASCII data files. Since these data are complex, they are stored as .CPX files. Each parameter Sij, Zij or Yij is stored in a single CPX file. Every file begins with a header starting with "#".
![]() Click here to learn more about the Port Definition Observable.
Click here to learn more about the Port Definition Observable.
To plot the S/Z/Y parameters, select a CPX data file from the Data Manager's 2D tab and click the Plot button. You can also plot the port characteristics from the navigation tree. Right-click on the Port Definition item in the "Observables" section of the navigation tree and select one of the items: Plot S Parameters, Plot Y Parameters, Plot Z Parameters, or Plot VSWR. By default, S-parameters are plotted as magnitude-phase Cartesian graphs, while Z and Y parameters are plotted as real-imaginary Cartesian graphs. You can also plot S parameters on a Smith chart. To change the graph type for a data file, select it in the Data Manager and click the Graph Props button. You will see a number of graphing options for each particular data file type. You can also change the graph scale from linear to dB-Field or dB-Power, and vice versa.
EM.Tempo and EM.Picasso can analyze periodic surfaces illuminated by a plane wave source. At the end of such simulations, the reflection and transmission coefficients of the periodic surface are calculated and written to complex-type ".CPX" files. These coefficients respectively represent the S11 and S21 parameters of a two-port network, where Ports 1 and 2 are in effect the top and bottom half-spaces.
Rational Interpolation of Port Characteristics
EM.Tempo computes the S/Z/Y parameters of your structure by taking a discrete Fourier transform (DFT) of the time-domain data generated during the FDTD time marching loop. The default number of frequency samples within the project's bandwidth is 200. This usually results in fairly smooth frequency response graphs. In contrast, the frequency-domain MoM engines of EM.Picasso and EM.Libera calculate the S/Z/Y parameters by performing a full-wave simulation at each individual frequency. Running a frequency sweep with 200 frequency samples wwould take a significant amount of computation time. With fewer frequency samples, on the other hand, the MoM solvers typically produce jagged frequency response graphs. One of way generating smooth frequency response graphs in EM.Picasso and EM.Libera is to run an adaptive frequency sweep.
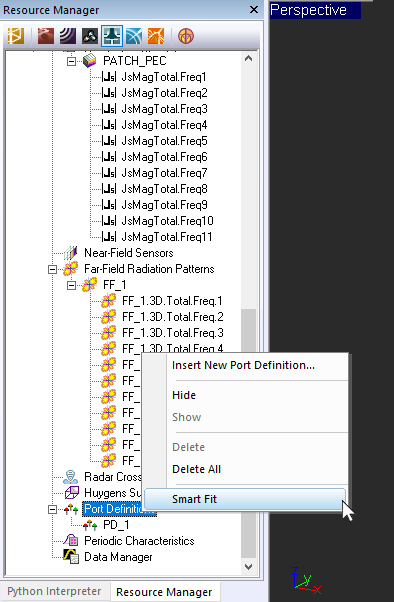
EM.Cube allows you to perform a rational-fit interpolation of the existing S/Z/Y parameter data as a post-processing operation without a need to run additional simulation engine runs. This operation generates new data files with lots of more intermediate data points which can produce a smooth graph. You can interpolate the scattering, impedance and admittance parameters either collectively or individually. You can do this post-processing operation from the navigation tree. Right-click on the Port Definition item in the Observables section of the navigation tree and select Smart Fit. At the top of the Smart Fit dialog, a drop-down list labeled Interpolate gives a list of all the available S/Z/Y parameter data for rational interpolation. The default option is "All Available Parameters". Then you see a box labeled Number of Available Samples, whose value is read from the data content of the selected complex-valued .CPX data file. Based on the number of available data samples, the dialog reports the Maximum Interpolant Order. You can choose any integer number for Interpolant Order, from 1 to the maximum allowed.
| |
Interpolant orders more than 15 often cause numerical instabilities even if you have a very large number of data samples. |
You can use the Update button of the dialog to generate the interpolated data for a given order. The new data are written to a complex data file with the same name as the selected S parameter and a "_RationalFit" suffix. While this dialog is open, you can change the interpolant order and regenerate the rational-fit data. You can plot the new data from the "2D Files" tab of Data Manager.
Probing Fields in Time and Frequency Domains
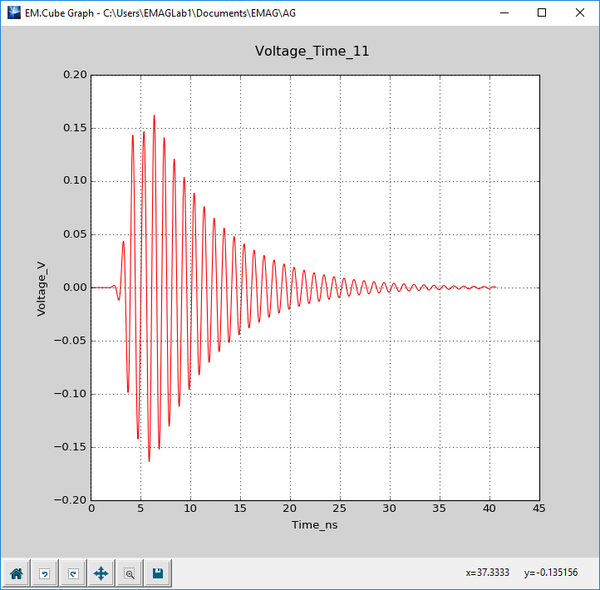
Field probes monitor and record the evolution of time-domain field components at a specified point in the computational domain. Only EM.Tempo offers the field probe observable. At the end of an FDTD simulation, the frequency spectrum of the field probe data is also computed using a discrete Fourier transform (DFT). Using field probes, you can examine the transient response of a system at a certain location. This is also very useful for monitoring the convergence of FDTD time marching loop. You can plot the time domain field components as a function of the time step index. You can also plot the spectral contents of those field components over the project's specified frequency bandwidth.
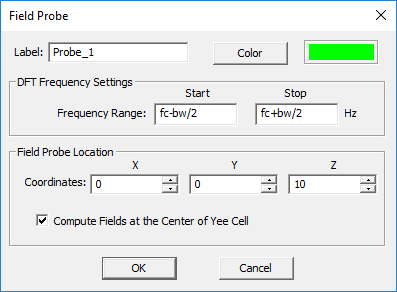
To define a new field probe, follow these steps:
- Right-click on the Field Probe item in the Observables section of the navigation tree and select Insert New Observable...
- You can change the default name of the probe as well as its color. The field probe is displayed as a small green arrow in the project workspace.
- By default EM.Tempo creates a field probe located at the origin of coordinates (0,0,0). You can move the probe to any location by changing its X, Y and Z coordinates.
- In the Probe Location section of the dialog, you can also set the Direction of the probe from a dropdown list that contains ±X, ±Y and ±Z options. The default direction is +Z.
At the end of an FDTD simulation, the electric and magnetic field components along the specified probe direction are saved at the probe's location. The time-domain fields from t = 0 to the last time step are written to real-valued data files with names "ProbeName_E_time.DAT" and "ProbeName_H_time.DAT". The frequency-domain spectrum data over the frequency range [fc - bw/2, fc + bw/2] are written to complex-valued data files with names "ProbeName_E_fre.CPX" and "ProbeName_H_fre.CPX". You can plot these data in EM.Grid, which can be accessed from the Data Manager. You have the option to change a field probe's start and end frequencies as long as they are within your FDTD excitation waveform's bandwidth.
Visualizing & Plotting Near-Field Distributions
In EM.Cube you can compute the electric and magnetic field distributions in a specific plane of the computational domain. For that purpose, you need to define a "Near-Field Sensor" observable for your project. All of EM.Cube's computational modules offer field sensor observables. However, the behavior of field sensors in EM.Cube's different computational modules is slightly different. In EM.Tempo and EM.Ferma, which have finite computational domains, the field sensor plane extends across the entire computational domain. In addition, the resolution of the field sensor data in these modules is determined by the project's mesh density. In EM.Picasso, EM.Libera, EM.Illumina and EM.Terrano, which feature unbounded background media, you can define field sensor planes of arbitrary size with an arbitrary number of sampling points.
For field sensor observables in EM.Tempo, you also need to specify a frequency for near-field computation. This frequency, by default, is the same as your project's center frequency (Fc), bit it can be different. In fact, you can define several field sensors at different frequencies as long as they are within the excitation source's bandwidth. At the end of an FDTD simulation, all the time domain electric and magnetic field values are available at all mesh nodes. These temporal quantities are transformed into the frequency domain using a discrete Fourier transform at the specified frequency to calculate the electric and magnetic fields on the specified sensor plane.
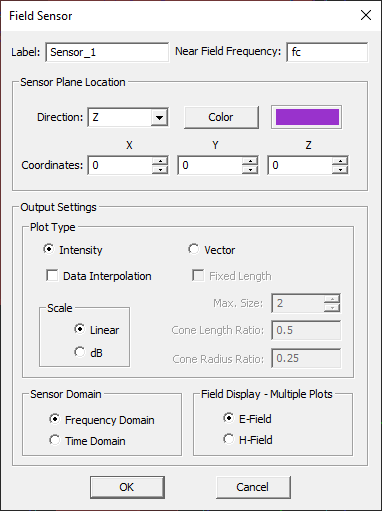
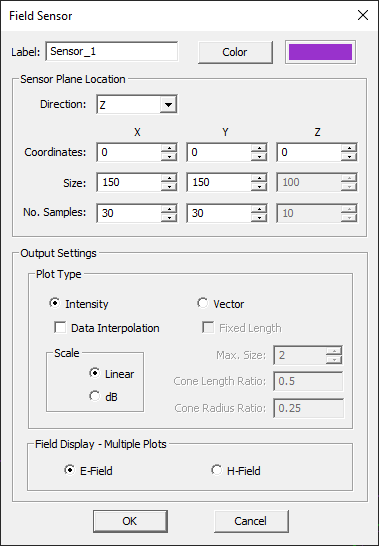
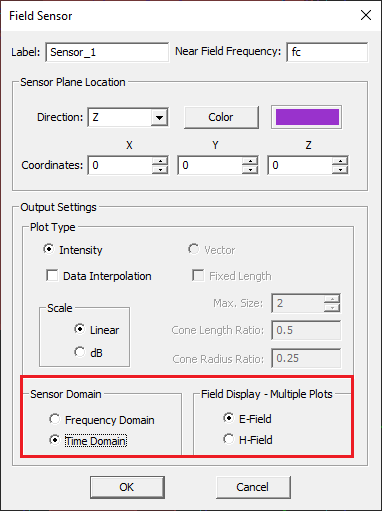
To define a new Field Sensor, follow these steps:
- Right click on the Field Sensors item in the Observables section of the Navigation Tree and select Insert New Observable...
- The Label box allows you to change the sensor’s name. you can also change the color of the field sensor plane using the Color button.
- Set the Direction of the field sensor. This is specified by the normal vector of the sensor plane. The available options are X, Y and Z, with the last being the default option.
- By default EM.Cube creates a field sensor plane passing through the origin of coordinates (0,0,0) and coinciding with the XY plane. You can change the location of the sensor plane to any point by typing in new values for the X, Y and Z coordinates. Keep in mind that you can move a sensor plane only along the specified direction of the sensor. Therefore, only one coordinate can effectively be changed. As you increment or decrement this coordinate, you can observe the sensor plane moving along that direction in the project workspace.
- In EM.Tempo and EM.Ferma, the sensor plane extends across the entire computational domain. In EM.Tempo, also specify the Near Field Frequency in the project's frequency unit.
- In EM.Picasso, EM.Libera, EM.Illumina and EM.Terrano, the initial size of the sensor plane is 100 × 100 project units. You can change the dimensions of the sensor plane to any desired size. You can also set the Number of Samples along the different directions. These numbers are equal to 10 by default.
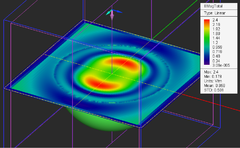
After closing the Field Sensor Dialog, the a new field sensor item immediately appears under the Observables section in the Navigation Tree and can be right clicked for additional editing. Once an FDTD simulation is finished, a total of 14 plots are added to every Field Sensor node in the Navigation Tree. These include the magnitude and phase of all three components of E and H fields and the total electric and magnetic field values at the specified frequency. Click on any of these items and a color-coded intensity plot of it is visualized in the project workspace. A legend box appears in the upper right corner of the field plot, which can be dragged around using the left mouse button. The values of the magnitude plots are normalized between 0 and 1. The legend box contains the minimum field value corresponding to 0 of the color map, maximum field value corresponding to 1 of the color map, and the unit of the field quantity, which is V/m for E-field and A/m for H-field. The values of phase plots are always shown in Radians between -π and π. To display the fields properly, the structure is cut through the field sensor plane, and only part of it is shown. If the structure still blocks your view, you can simply hide or freeze it. You can change the view of the field plot with the available view operations such as rotating, panning, zooming, etc.
At the end of a simulation, the field data are written into a 3D data file with a .SEN file extension. The field sensor node in the navigation tree is then populated with a total of 14 field data plots: magnitude and phase plots for each of the three components of the electric and magnetic fields (Ex, Ey, Ez, Hx, Hy, Hz), plus the total electric field and total magnetic field plots on the specified plane. EM.Ferma's field sensors display a total of 16 plots, 14 electric and magnetic field plots plus one for the electric scalar potential and another for the magnitude of the total magnetic vector potential. Note that in EM.Ferma, the electrostatic or magnetostatic field values are real-valued.
The legend of a field plot shows the minimum and maximum field values, the field unit (V/m for electric and A/m for magnetic) as well as the mean field and the standard deviation. The electric scalar potential and magnetic vector potential have units of V and A, respectively. The total electric and magnetic fields and the total magnetic vector potential are defined in the following manner:
[math] | \mathbf{E_{tot}} | = \sqrt{|E_x|^2 + |E_y|^2 + |E_z|^2}[/math]
[math] | \mathbf{H_{tot}} | = \sqrt{|H_x|^2 + |H_y|^2 + |H_z|^2}[/math]
[math] | \mathbf{A_{tot}} | = \sqrt{|A_x|^2 + |A_y|^2 + |A_z|^2}[/math]
EM.Cube offers two different ways of visualizing electric and magnetic fields: as a intensity plot or a vector plot. The first type shows the field amplitude and phase using small colored pixels. The pixel size is equal to the mesh cell size in the case of EM.Tempo and EM.Ferma and it is specified and controlled by user in the case of EM.Cube's other computational modules. The second type is a vector plot showing arrows (or cones) directed along the visualized field component. In the case of the total electric and magnetic fields, the cone plots show the overall direction of the fields at any point on the sensor plane. To set the type of a field plot, open the field sensor's property dialog by right clicking its name in the Navigation Tree and selecting Properties... from the contextual menu. In the Plot Type section, choose one of the two radio buttons labeled Intensity or Vector. In the former case, you may also check the box labeled Data Interpolation, which is unchecked by default. This will convert the pixelized confetti map into a smooth intensity plot using data interpolation. In the latter case, you can set the size of the vector arrows using the box labeled Max Size or set the Cone Length Ratio and Cone Radius Ratiowith respect to the total arrow length.
Field plots (total, magnitude, phase, etc.) are displayed with some default settings and options, which can be further customized individually. To do so, open the Output Plot Settings dialog by right clicking on a specific plot entry in the Navigation Tree and selecting Properties... or by double clicking on the surface of the plot's legend box. Two scale options are available: Linear and dB. With the (default) linear option selected, the field is always mapped between the minimum and maximum total field values in that plane. If the dB option is selected, the field component is normalized to the maximum total field value and then converted to the dB scale. You can hide the legend box by deselecting the box labeled Show Legend Box. The plot bounds can be set individually for every field plot. In the Limits section of the plot's property dialog, you see four options: Default, User Defined, 95% Conf. and 95% Conf.. Select the user defined option and enter new values for the Lower and Upper limits. The last two options are used to remove the outlier data within the 95% and 99% confidence intervals, respectively. In other words, the lower and upper limits are set to μ ± 1.96σ and μ ± 2.79σ , respectively, assuming a normal distribution of the data.
You can also choose from three color maps offered in the plot's property dialog: Rainbow, Basic and Gray Scale.
Plotting Field Distribution Graphs Along Lines
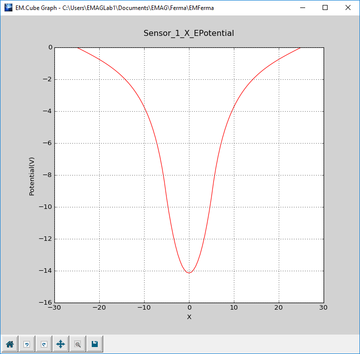
Each field sensor observable has two linear axes (crosshairs) that are placed at the center of its rectangular plane by default when your define it for the first time. At the end of a simulation, besides the 3D near-field data visualization, a number of 2D data files are added to your project folder corresponding to each field sensor. Theses include the total electric and magnetic field distributions along the two crosshairs. Their names has the form: "SensorName_T_ETotal.DAT" and "SensorName_T_HTotal.DAT", where the letter "T" is either X or Y or Z depending on the direction of the crosshair.
You can change the location of the orthogonal crosshairs from the Field Sensor dialog. Since the field sensor are always parallel to one of the three principal planes, they have the form X = const, or Y = const, or Z = const. Therefore, the two other coordinate are free to move on the sensor plane. In the "Sensor Plane Location" section of the Field Sensor dialog, one of the three Coordinate boxes controls the location of the sensor plane, while the other two boxes control the location of the two crosshairs.
In the case of electrostatic and magnetostatic simulations in EM.Ferma, additional data files are generated for the electric scalar potential and the magnitude of the total magnetic vector potential. These are called "SensorName_T_EPotential.DAT" and "SensorName_T_HTotal.DAT", respectively. Note that the total vectorial quantities are always positive but the electric scalar potential can be negative.
Visualizing & Plotting Current Distributions
Of EM.Cube's computational modules, EM.Picasso and EM.Libera feature the method of moments (MoM) and EM.Illumina features the physical optics (PO) method. All these methods involve integral equation formulations of Maxwell's equations based on electric and magnetic surface currents. Perfect electric conductor (PEC) surfaces are modeled by electric surface currents (J). EM.Illumina models perfect magnetic conductor (PMC) surfaces by magnetic surface currents (M). Impedance surfaces are modeled using a combination of both electric and magnetic surface currents. Similarly, EM.Libera's Surface MoM engine models dielectric materials using a combination of both electric and magnetic surface currents. EM.Picasso models slot traces using magnetic surface currents. In EM.Tempo, EM.Ferma and EM.Terrano, the principal computed solutions are electric and/or magnetic field quantities, while in EM.Illumina, EM.Picasso and EM.Libera, the principal computed solutions are electric and/or magnetic current quantities.
In order to visualize the current distributions, you need to define current distribution observables in the Navigation Tree of your project. At the end of a simulation, the current data are written into a 3D data file with a .CUR file extension. The current distribution node in the Navigation Tree is then populated with a total of 14 current data plots: magnitude and phase plots for each of the three components of the electric and magnetic surface currents (Jx, Jy, Jz, Mx, My, Mz), plus the total electric current and total magnetic current plots. In this regard, current distribution plots are very similar to field distribution plots. The legend of a current distribution plot shows the minimum and maximum current values, the surface current units (A/m for electric and V/m for magnetic) as well as the mean current and the standard deviation. Similarly, from the property dialog of the current distribution plot, you can change the plot type between intensity and vector types.
The total electric and magnetic currents are defined in the following manner:
[math] | \mathbf{J_{tot}} | = \sqrt{|J_x|^2 + |J_y|^2 + |J_z|^2}[/math]
[math] | \mathbf{M_{tot}} | = \sqrt{|M_x|^2 + |M_y|^2 + |M_z|^2}[/math]
In both EM.Libera and EM.Illumina, you need to define a single current distribution observable to visualize all the available currents. In EM.Picasso, you need to define a current distribution observable for each individual trace of your planar structure. This is due to the fact that the substrate layers of a planar structure might be placed very close to each other, and simultaneous display of all the current distribution maps on top of each other may not be helpful. The main difference between current distribution and field distribution plots is that the former is visualized on the mesh of the structure, while the latter is always computed and visualized on predefined planes. Sometimes when visualizing the current distributions on a highly curved surface like a sphere, you may find parts of the plot hidden underneath the curved surface. In such cases, you can freeze the CAD objects to move them out of the way, or enable the mesh view mode and plot the current distribution overlaid on the mesh of the structure.
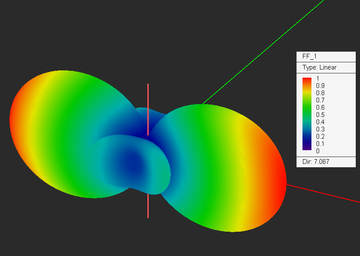
Visualizing & Plotting Far-Field Radiation Patterns
Once an simulation is finished, three far-field items are added to the Far Fields section of the Navigation Tree. These are the far-zone E-field component along φ direction, the far-zone E-field component along φ direction and the total far-zone E-field defined as:
- [math]|\mathbf{E_{ff,tot}}| = \sqrt{| E_{\theta}|^2 + |E_{\phi}|^2 }[/math]
![]() Click here to learn more about the theory of Far-field Radiation Patterns.
Click here to learn more about the theory of Far-field Radiation Patterns.
The 3D plots can be viewed in the project workspace by clicking on each item. The view of the 3D far field plot can be changed with the available view operations such as rotate, pan and zoom. A legend box appears in the upper right corner of the 3D radiation pattern plot, which can be dragged around with the left mouse button. The (maximum) directivity of the radiating structure is displayed at the bottom of the legend box.
Note that the 3D radiation patterns are always plotted to be centered at the origin (0,0,0) of the world coordinate system. In other words, no matter where you radiator is located in the project workspace, the radiation patterns are calculated with respect to the standard spherical coordinate system. Since the 3D radiation patterns are scaled to the maximum total magnitude, the cross-polarization component might sometimes be too small to be clearly visible, and you may need to zoom in the plot to see it.
You can also change the type of the 3D radiation pattern plot through the Radiation Pattern Dialog. In the 3D Display Type section of this dialog you can choose from three options: 3D Polar, which is the default choice, Spherical Map and Vector. You can set the resolution of the radiation pattern plot along both theta and phi directions. By default, angle increments are 5°. In the case of antenna array structures with many side lobes and fine details, you may need to define a higher resolution, e.g., 1°. You can change the properties of a 3D radiation pattern plot by right clicking on the plot's name in the Navigation Tree and selecting the Properties...from the contextual menu or by double-clicking on the surface of the legend box. This dialog is very similar to those of field distribution and current distribution plots. For example, you can change the scale of the pattern plot from linear to dB.
At the end of a simulation with a fear-field observable, the radiation pattern data Eθ, Eφ and Etot in the three principal XY, YZ and ZX planes plus one additional user defined phi plane cut are written into output data files and are available for plotting as 2D graphs in EM.Grid. There are a total of eight 2D pattern graphs in the data manager: 4 polar graphs and 4 Cartesian graphs of the same pattern data. The polar pattern data files have a .ANG file extension, while the Cartesian pattern data files have a .DAT file extension. You can plot these 2D pattern graphs either from Data Manager or directly from the Navigation Tree by right-clicking on the Far Fields node of the tree and selecting the desired plot from the contextual menu.
At the end of a sweep simulation, other radiation characteristics are also computed as a function of the sweep variable (frequency, angle, or any other user defined variable). These include the Directivity (D0), Total Radiated Power (PRAD) and other specified radiation characteristics such as radiation efficiency, half-power beam width (HPBW), maximum side lobe level (SLL), etc. Directive Gain (DG) as a function of the θ and φ angles is also available. Another radiation characteristic of interest especially in circularly polarized scenarios is the Axial Ratio. In EM.Cube, the axial ratio is always defined in the LCPz or RCPz sense based on the X- and Y-components of the electric field. In order to calculate the directive gain or axial ratio, you have to check the boxes labeled Axial Ratio (AR) or Directive Gain (DG) in the "Additional Radiation Characteristics" section of the Radiation Pattern Dialog. Four 2D Cartesian graphs of the axial ratio as functions of the theta angle are generated in the three principal XY, YZ and ZX planes as well as the additional user defined phi plane cut. At the end of a sweep simulation, the directive gain and axial ratio can also be plotted as functions of the sweep variable. In that case, either quantity needs to be computed at a fixed pair of θ and φ angles. These angles are specified in degrees as Custom Azimuth & Elevation Angles in the "Output Settings" section of the Radiation Pattern Dialog. The default values of the user defined azimuth and elevation are both zero.
Using Array Factor to Model Antenna Arrays
EM.Cube can model antenna arrays in two different ways. The first approach is full-wave and requires building an array of radiating elements using the Array Tool and feeding individual array elements using some type of excitation. This method is very accurate and takes into account all the inter-element coupling effects. The second method is based on the concept of "Array Factor" and ignores inter-element coupling effects. In this approach, you can regard the structure of the project workspace as a single radiating element and specify an array grid with the number of elements and element spacing along the X, Y, Z directions. At the end of s simulation, the specified array factor is calculated and multiplied by the element pattern to estimate the radiation pattern of the overall antenna array.
![]() Click here to learn more about the theory of Array Factor.
Click here to learn more about the theory of Array Factor.
To define an array factor, open the Radiation Pattern Dialog of the project. In the section titled Impose Array Factor, you will see a default value of 1 for the Number of Elements along the three X, Y and Z directions. This implies a single radiator, which is your structure in the project workspace. There are also default zero values for the Element Spacing along the X, Y and Z directions. You should change both the number of elements and element spacing in the X, Y or Z directions to define any desired finite array lattice. Note that using an array factor for far field calculation, you cannot assign non-uniform amplitude or phase distribution to the array elements. For this purpose, you have to define an array object.
The radiation patterns of antenna arrays usually have a main beam and several side lobes. Some parameters of interest in such structures include the Half Power Beam Width (HPBW), Maximum Side Lobe Level (SLL) and First Null Parameters such as first null level and first null beam width. You can have EM.Cube calculate all such parameters if you check the relevant boxes in the "Additional Radiation Characteristics" section of the Radiation Pattern Dialog. These quantities are saved into ASCII data files of similar names with .DAT file extensions.
| |
Defining an array factor in the radiation pattern dialog simply performs a post-processing calculation. The computed far field obviously does not take into account any inter-element coupling effects as EM.Cube does not construct a real physical array in the project workspace. |
Far Field Data Files
At the end of a simulation, the far field radiation pattern data in the entire 3D space are written into an output ASCII data file with a .RAD file extension. This file is particularly important because you can use it in EM.Terrano as the radiation pattern file of a transmitter or receiver. All transmitters and receivers in EM.Terrano require a ".RAD" radiation file as part of their definition.
The far field data represent the actual electric field in V/m measured in the far field region of the radiating structure at a distance of one meter from the origin of the World Coordinate System. Note that the spherical factor exp(-jkr)/r is removed from the far field data. In other words, the far field is normalized to r, the distance from the field observation point to the origin.
The radiation file starts with a header section consisting of several comment lines that start with “#”. Two of these lines contain the values of Total Radiated Power and Directivity. The body of the data file consists of seven columns which are separated by a space character. These columns represent:
- Angle Phi in radians
- Angle Theta in radians
- Real part of the Theta component of electrical field in V/m
- Imaginary part of the Theta component of electrical field in V/m
- Real part of the Phi component of electrical field in V/m
- Imaginary part of the Phi component of electrical field in V/m
- Total magnitude of far-zone electric field in V/m
If you define an RCS observable instead of a radiation pattern observable, a 3D output ASCII data file with a .RCS file extension is generated which contains the RCS values along the theta and phi directions along with the total RCS.
Visualizing & Plotting Radar Cross Section
When the physical structure is illuminated by a plane wave source, the calculated far field data indeed represent the scattered fields. In the context of radar systems, the incident plane wave can be regarded as a transmitted signal to intercept a target. The scattered field can be regarded as the target's echo signal. A target is usually characterized by a quantity called the Radar Cross Section (RCS), which gives a measure of its effective surface area as seen by a radar system.
![]() Click here to learn more about the theory of Radar Cross Section .
Click here to learn more about the theory of Radar Cross Section .
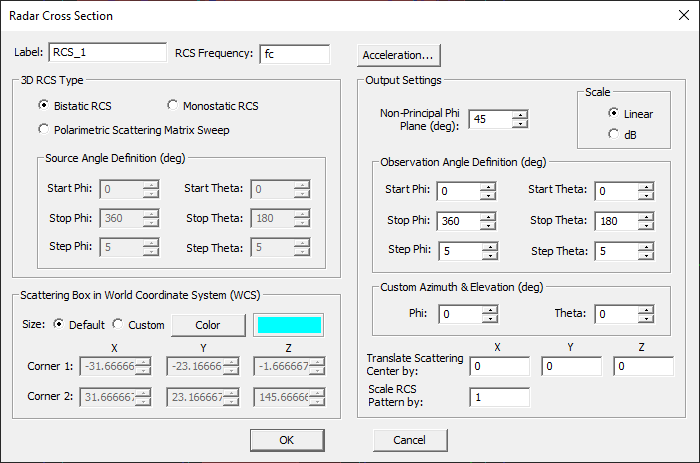
To compute the RCS of your physical structure, you must define an RCS observable instead of a radiation pattern observable. To do so, follow the steps below:
- Right click on the Far Fields item in the Observables section of the Navigation Tree and select Insert New RCS... to open the Radar Cross Section Dialog.
- Use the Label box to change the name of the far field or change the color of the far field box using the Color button.
- The frequency of RCS calculation can be specified in the box labeled Far Field Frequency. By default, this is equal to the center frequency of the project. However, you can calculate the far field data at any other frequency within the project's frequency range.
- The resolution of RCS calculation is specified by Angle Increment expressed in degrees. By default, the θ and φ angles are incremented by 5 degrees.
- Define the desired box for far field calculations in the Scattering Box section of the dialog. As in the case of radiation pattern, there are two options available, a default radiation box (radio button Size: Default) or a user defined radiation box (radio buttons Size: Custom). If you check Size: Default, no radiation box corner coordinates need to be specified. The radiation box will always be 0.1 free space wavelength away from the bounding box of the entire physical structure. Select Size: Custom to set the far field box manually. The values for the coordinates of Corner 1 and Corner 2 can now be changed. Corner 1 is the lower-front-left corner and Corner 2 is the upper-rear-right corner of the radiation box. The dimensions are entered in world coordinate system (WCS).
- At the end of an FDTD simulation, besides calculating the RCS data over the entire (spherical) 3D space, a number of 2D RCS graphs are also generated. These are indeed RCS cuts at certain planes, which include the three principal XY, YZ and ZX planes plus one additional constant φ-cut. This latter cut is at φ = 45° by default. You can assign another φ angle in degrees in the box labeled Non-Principal Phi Plane.
At the end of an FDTD simulation, in the far field section of the Navigation Tree, you will have the θ and φ components of RCS as well as the total radar cross section: σθ, σφ, and σtot. The RCS values (σ) are expressed in m2. The 3D plots are normalized to the maximum RCS value, which is displayed in the legend box. The 2D RCS graphs can be plotted in EM.Grid exactly in the same way that you plot 2D radiation pattern graphs. A total of eight 2D RCS graphs are available: 4 polar and 4 Cartesian graphs for the XY, YZ, ZX and user defined plane cuts. at the end of a sweep simulation, EM.Cube calculates some other quantities including the backscatter RCS (BRCS), forward-scatter RCS (FRCS) and the maximum RCS (MRCS) as functions of the sweep variable. In this case, the RCS needs to be computed at a fixed pair of φ and θ angles. These angles are specified in degrees as User Defined Azimuth & Elevation in the "Output Settings" section of the Radar Cross Section Dialog. The default values of the user defined azimuth and elevation are both zero corresponding to the bore sight.
The 2D RCS graphs can be plotted in EM.Grid exactly in the same way that you plot 2D radiation pattern graphs. A total of eight 2D RCS graphs are available: 4 polar and 4 Cartesian graphs for the XY, YZ, ZX and user defined plane cuts. At the end of a sweep simulation, EM.Cube calculates some other quantities including the back-scatter RCS (BRCS), forward-scatter RCS (FRCS) and the maximum RCS (MRCS) as functions of the sweep variable (frequency, angle, or any user defined variable). The output parameters BRCS and MRCS represent the total back-scatter RCS and maximum total RCS of your target structure when it is excited by an incident plane wave source at the specified θs and φs source incidence angles. FRCS, on the other hand, is the total forward-scatter RCS measured at the user-specified θo and φo observation angles. These angles are specified in degrees as Custom Azimuth & Elevation Angles in the "Output Settings" section of the Radar Cross Section Dialog. The default values of the custom azimuth and elevation angles are both zero.
3D Field Animation
At the end of a sweep simulation (a frequency sweep, angular sweep, parametric sweep, etc.), if you have defined a field sensor or a current distribution or a far field observable (either radiation pattern or RCS) in your project, a number of 3D plots are generated for all samples of the sweep variable. Each field sensor or current distribution normally has 14 field maps for the amplitude and phase of all the three components of E- and H-fields plus the magnitude of the total fields. Each far field observable has three spherical plots corresponding to the θ and φ components of the far field and the total far field. During a sweep simulation, only the total field plots are generated and added to the Navigation Tree. This is done to avoid cluttering the Navigation Tree. For field sensors, the total electric field plot is stored by default. For current distribution observables, the total electric surface current plot is stored by default. You can change the settings of the field sensor to store the total magnetic field plot during sweep simulations. You can also change the settings of the current distribution observable to store the total magnetic surface current plot during sweep simulations.
After a sweep simulation is completed, you will have a list of total fields, or total currents, or total radiation patterns, or total RCS. You can click on each of these plots to view them in the project workspace. If you highlight the first plot in the list, you can use the keyboard's up and down arrow keys to move from one plot to another. Or you can use EM.Cube's animation feature for this purpose. Animation in EM.Cube consists of sequential display of the plots in the main window at a preset speed. To animate the 3D plots, right click on the observable's name in the Navigation Tree and select Animation from the contextual menu. The 3D plots start to animate beginning with the first sample, going through all the plots one by one until the last one and repeating the loop all over again. While the animation proceeds in the main window, a dialog titled Animation Controls Dialog pops up at the lower right corner of the screen. You can set the speed of animation by typing in a value for Rate, which is indeed the frame duration expressed in multiples of 100 milliseconds. The default frame duration is 300 msec.
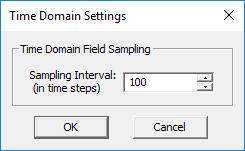
In the course of the FDTD time marching process, a tremendous amount of data are generated that include all the six E/H field components at every Yee cell and at every time step. The temporal field values at a sensor plane are of particular interest. Such plots show the evolution of the fields as a function of time starting from time t = 0, when all the fields are zero everywhere in the computational domain. EM.Tempo can record snapshots of the field sensor data as the time loop marches forward. When you define a field sensor for the first time, by default it displays the frequency domain near field data. In order to record and save the time domain data, you have to open the field sensor's property dialog. In the section titled Sensor Domain, select the radio button labeled Time Domain. Also, in the section titled "Field Display - Multiple Plots", select one of the two radio buttons labeled E-Field or H-Field. By default, the time domain field data are saved every 100 time steps. To change this setting, right-click on the Field Sensors item in the navigation tree and select Time Domain Settings... from the contextual menu. In the Time Domain Settings Dialog, change the value of the box labeled Sampling Interval (in time steps).
Time domain animation is available only for FDTD simulations of "Analysis" type. It cannot be used in conjunction with sweep simulations. Once the FDTD Analysis is finished, you can click any of the field plots and visualize it in the main window or you can animate them by right-clicking on the field sensor's name in the navigation tree and selecting Animation from the contextual menu. You can change the animation settings from the Animation Controls Dialog. Note that the animation loop repeats itself indefinitely until you close the Animation Controls dialog or hit the keyboard’s Esc key.
Building New Data Files from Scratch
Data files in EM.Cube are generated in many different ways. Earlier you saw how various near-field and far-field simulation data or port characteristics are generated, visualized or plotted on different types of graphs at the end of an EM.Cube simulation. By defining custom output parameters in arbitrary ways, you can generate many new data files at the end of parametric sweeps. In addition, EM.Cube lets you build new data files of the following types from scratch:
- 2D real data files with a .DAT extension
- 3D Cartesian data files with a .CAR extension
The above file types are generally created using arithmetic operations and mathematical expressions. In the case of a real data file, first you generate the X column and then produce the Y column typically as a function of X. In the case of a Cartesian data file, you set up a rectangular grid in the 3D space and then define data values on the grid typically as a function of the grid coordinates (x, y, z).
Using Data Manager to Create New Data Files
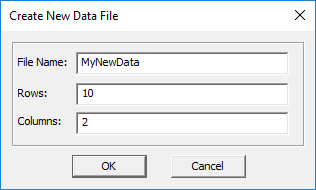
EM.Cube's Data Manager lets you generate blank data files that you can fill with data later. You can also modify the contents of data files using a large number of editing and computing tools. Click the New button of Data Manager's 2D Data Files tab to create a new real-valued data file with a .DAT file extension. The "Create New Data File" dialog asks for a file name, number of rows and number of columns. A new data file is immediately opened in a Data Manager spreadsheet that shows columns of zeros. The name of the new data file is added to the Data Manager's file list in the 2D Data Files tab. You can also use the New button of Data Manager's 3D Data Files tab to create different types of 3D data files as will be discussed later.
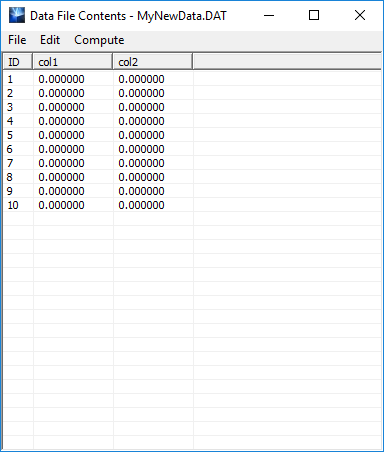
It is your responsibility to supply the contents of a new data file. You can do this manually using Data Manager's native text editor, or in Windows Notepad, or do it systematically using Data Manager's "Compute" feature discussed next. You can open Data Manager's Text Editor from any spreadsheet's Edit Menu. In the example shown below, we create a new data file called "MyNewData.DAT" with 2 columns and 10 rows all initially set equal to zero.
Using Spatial Data Generator to Create New 3D Data
Clicking the New button of Data Manager's 3D Data Files tab opens up EM.Cube's Data Generator. You can also open EM.Cube's data Generator by selecting the menu item Simulate → Spatial Data Generator... This utility can be used to create new 3D data files of Cartesian type. When you open the Data Generator, by default a 3D Cartesian data file is assumed with a real scalar data column. A default rectangular grid of dimensions 10 units by 10 units in the XY plane is considered with step values of 1 along both X and Y. The data column is filled with zeros. In the box labeled Value enter a mathematical expression for your data. This can be any mathematical expression involving the node coordinates x, y, z. You can use standard and library functions as well as you own Python functions to define the expression. Click the Apply button to update the contents of the Data column. Note that using the drop-down list labeled Column, you can even change the contents of the x, y, z columns.
In general, you can define the following types of data in the Data Generator:
- Real Scalar: adds one additional data column.
- Complex scalar: adds two additional data columns for real and imaginary parts.
- Real vector: adds three additional data columns for the X, Y, Z vector components.
- Complex vector: adds six additional data columns for the real and imaginary parts of the X, Y, Z vector components.
- Isotropic Material: adds four additional data columns for permittivity, permeability, electric conductivity and magnetic conductivity.
- No Data: adds no additional data column.
![]() Click here to see a List of Library Functions.
Click here to see a List of Library Functions.
![]() Click here to learn more about Python's Standard & Advanced Mathematical Functions.
Click here to learn more about Python's Standard & Advanced Mathematical Functions.
![]() Click here to learn more about Creating Custom Python Functions.
Click here to learn more about Creating Custom Python Functions.
In the example shown in the figure below, a real scalar quantity has been defined by the expression "(x^+y^2)/10" over the 11 × 11 grid.
After you close the data generator dialog, the new Cartesian data file is added to the Data Manager's list of 3D data files. If you select this data file and click the Plot button of the data manager dialog, a 3D visualization of the Cartesian data appears in CubeCAD's main window.
Visualizing 3D Data in CubeCAD
Besides "Geometrical Construction", CubeCAD also has a "Data Visualization" section in its navigation tree. From here you can visualize the 3D data files that you have created using the Data Generator. The Data Visualization section of CubeCAD's navigation tree has a node titled Cartesian Data. When you plot a 3D Cartesian data file with a ".CAR" file extension, the name of the plot is added under this node.
You can also create a new 3D Cartesian data entry under the Cartesian Data node of the navigation tree and then import a data file for it. For this purpose, follow the steps below:
- Right-click on the Cartesian Data item of CubeCAD's navigation tree and select Insert New Observable... from the contextual menu.
- A new Data Visualization dialog opens up where you can specify the desired visualization type, e.g. intensity vs. vector, etc.
- After closing the dialog, the standard Windows Open Dialog opens up where you can browse your folders to import a data file. The default file extension is set to .CAR. Select the desired data file and click the Open button of the dialog to import the data.
- A 3D visualization of the imported data file appears in the project workspace.
- Select any item from these node to visualize it in the project workspace.
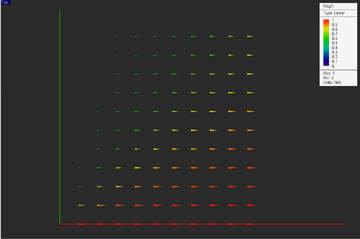
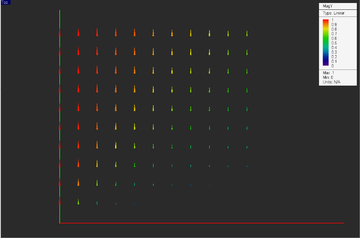
As an example, a real vector data file has been defined as shown in the figure below. This is indeed the definition of the unit radial vector in the polar coordinates:
[math] \mathbf{\hat{r}} = \cos\phi \mathbf{\hat{x}} + \sin\phi \mathbf{\hat{y}} = \frac{x}{\sqrt{x^2+y^2}} \mathbf{\hat{x}} + \frac{y}{\sqrt{x^2+y^2}} \mathbf{\hat{y}} [/math]
For this data set, the output plot type is set to Cone as opposed to the default Intensity type. The maximum cone size is set to 0.5. This is done through the Cartesian data visualization dialog, which can be accessed from the contextual menu of the data entry in the navigation tree.
The figures below show the 3D visualizations of the Vx and Vy components as well as the total vector magnitude.