The Far-Field Approximation for Radiation & Scattering Problems
![]() Back to Maxwell's Equations Page
Back to Maxwell's Equations Page
Contents
Transverse Electromagnetic Waves
Electromagnetic waves are synchronized oscillations of electric and magnetic fields that propagate at the speed of light through a vacuum. The oscillations of the two fields are perpendicular to each other and perpendicular to the direction of energy propagation. The wavefront of electromagnetic waves emitted from a point source is spherical. As the wave propagates away from its source, its field amplitudes decay as 1/R, where R is the distance between the source and observation points. At far enough distances from the source, the wave is reduced to a transverse electromagnetic (TEM) wave with a planar wavefront. The electric and magnetic field vectors of a TEM wave satisfy the following equation:
[math] \mathbf{H(r)} = \frac{1}{\eta_0} \mathbf{\hat{k}} \times \mathbf{E(r)} [/math]
where [math]\mathbf{\hat{k}}[/math] is the propagation vector, and η0 = 120π Ω is the intrinsic impedance of the free space.
In a spherical coordinate system where the source is located at the origin of coordinates, the propagation vector can be written as:
[math] \mathbf{\hat{k}} = \mathbf{\hat{r}} [/math]
where [math]\mathbf{\hat{r}}[/math] is the unit radial vector. Then the transverse field components of a TEM wave satisfy the following relations:
[math] H_\theta = -\frac{E_\phi}{\eta_0}, \quad H_\phi = \frac{E_\theta}{\eta_0} [/math]
Definition of the Far Radiation Zone
In general, by far fields we mean the electric fields evaluated in the far zone of a physical structure, which satisfies the following condition:
[math]r \lt\lt \frac{2D^2}{\lambda_0}[/math]
where r is the distance between the observation and source points, and D is the largest dimension of the radiating structure. In EM.Cube, the far-zone electric fields Eff(θ, φ) are functions of the spherical observation angles only and are defined as
[math] \begin{align} & \mathbf{E(r) = E} (r,\theta,\phi) = \frac{e^{-jk_0 r}}{r} \mathbf{E^{ff}}(\theta,\phi) \\ & \mathbf{H(r) = H} (r,\theta,\phi) = \frac{1}{\eta_0} \mathbf{ \hat{r} \times E^{ff}(r) } \end{align} \quad k_0 r \gt\gt 1 [/math]
where k0 = 2π/λ0.
Computing the Far-Zone Fields from Near-Zone Field Data
EM.Tempo's FDTD engine calculates the far fields using a near-field-to-far-field transformation of the field quantities on a given closed surface, which is denoted the radiation box. You can use EM.Cube's default radiation box or define your own. EM.Picasso, EM.Libera and EM.Illumina compute the far fields directly by integrating the electric and magnetic surface current solutions to the numerical problem. The far-zone electric field can be written as:
[math] \mathbf{E^{ff}(r)} = \frac{jk_0 e^{-jk_0 r}}{4\pi r} \left\{ \eta_0 \mathbf{ \hat{r} \times \hat{r} } \times \iint_{S_J} \mathbf{J(r')} e^{jk_0 \mathbf{\hat{r}\cdot r'}} ds' + \mathbf{\hat{r}} \times \iint_{S_M} \mathbf{M(r')} e^{jk_0 \mathbf{ \hat{r} \cdot r' } } ds' \right\} [/math]
where J and M are either the actual electric and magnetic surface currents on the surface of your physical structure, or the equivalent electric and magnetic surface currents on the surface of the enclosing radiation box. One can define a pair of electric and magnetic radiation integrals:
[math] \begin{align} & \mathbf{N(r)} = \iint_S \mathbf{J(r')} e^{ jk_0 \mathbf{\hat{r} \cdot r'} } \, ds' \\ & \mathbf{L(r)} = \iint_S \mathbf{M(r')} e^{ jk_0 \mathbf{\hat{r} \cdot r'} } \, ds' \\ \end{align} [/math]
where
[math] \mathbf{\hat{r}} = \sin\theta \cos\phi \mathbf{\hat{x}} + \sin\theta \sin\phi \mathbf{\hat{y}} + \cos\theta \mathbf{\hat{z}} [/math]
In that case, the θ and φ components of the far fields can be computed from the following relationships:
[math] \begin{align} & E_{\theta}^{ff}(\theta, \phi) = -\frac{jk_0}{4\pi} (L_{\phi} + \eta_0 N_{\theta}) \\ & E_{\phi}^{ff}(\theta, \phi) = \frac{jk_0}{4\pi} (L_{\theta} + \eta_0 N_{\phi}) \end{align} [/math]
where the θ and φ components of the radiation integrals are given by:
[math] \begin{align} & N_{\theta}(\theta,\phi) = \iint_S [J_x\cos\theta\cos\phi + J_y\cos\theta\sin\phi - J_z\sin\theta] e^{ jk_0 \mathbf{\hat{r} \cdot r'} } \, ds' \\ & N_{\phi}(\theta,\phi) = \iint_S [-J_x \sin\phi + J_y\cos\phi] e^{ jk_0 \mathbf{\hat{r} \cdot r'} } \, ds' \end{align} [/math]
[math] \begin{align} & L_{\theta}(\theta,\phi) = \iint_S [M_x\cos\theta\cos\phi + M_y\cos\theta\sin\phi - M_z\sin\theta] e^{ jk_0 \mathbf{\hat{r} \cdot r'} } \, ds' \\ & L_{\phi}(\theta,\phi) = \iint_S [-M_x \sin\phi + M_y\cos\phi] e^{ jk_0 \mathbf{\hat{r} \cdot r'} } \, ds' \end{align} [/math]
Radiated Power & Directivity
In calculating the far field quantities, using Poynting's theorem, one can define the radiated power density as:
[math] \mathbf{W} = \frac{1}{2} \text{Re}(\mathbf{E \times H^*}) = \frac{\mathbf{\hat{k}}}{2\eta_0} |\mathbf{E}(r,\theta,\phi)|^2 \, |_{r \to \infty} [/math]
To eliminate the dependency on r, a normalized quantity called "Radiation Intensity" is defined in the following way:
[math] S(\theta,\phi) = \lim_{r \to \infty} r^2 |\mathbf{W}| = \frac{1}{2\eta_0} | \mathbf{E^{ff}}(\theta,\phi)|^2 [/math]
The total radiated power can now be calculated as:
[math] P_{rad} = \int\limits_0^{2\pi} d\phi \int\limits_0^{\pi} d\theta \, S(\theta,\phi) \sin\theta = \frac{1}{2\eta_0} \int\limits_0^{2\pi} \int\limits_0^{\pi} |\mathbf{E^{ff}}(\theta,\phi)|^2 \sin\theta \, d\theta \, d\phi [/math]
The (maximum) Directivity of the radiating structure is calculated using the definition:
- [math] D_0 = \frac{4\pi [S(\theta,\phi)]_{max}}{P_{rad}} = \frac{ 4\pi \big| \mathbf{E^{ff}}(\theta,\phi) \big|^2 |_{max} } { \int\limits_0^{2\pi} \int\limits_0^{\pi} \big| \mathbf{E^{ff}}(\theta,\phi) \big|^2 \sin\theta \,d\theta \,d\phi } [/math]
Array Factor
Consider an antenna structure whose radiation center is situated at the origin of the spherical coordinate system (0, 0, 0) and has a far-zone electric field E0ff(θ, φ). If you translate this structure to a new arbitrary point (xi, yi, zi), its far field is transformed in the following way:
[math] \mathbf{E_i^{ff}}(\theta,\phi) = \mathbf{E_0^{ff}}(\theta,\phi) e^{jk_0 \left( x_i sin \theta cos \phi + y_i sin \theta sin \phi + z_i cos \theta \right) } [/math]
In the most general sense, an antenna array consists of a set of N identical radiating elements located at coordinates (xi, yi, zi) and excited with complex weight coefficients wi. Using the principle of linear superposition, the far-zone electro field of the overall antenna array can be expressed as:
[math] \mathbf{E_{tot}^{ff}}(\theta,\phi) = \mathbf{E_0^{ff}}(\theta,\phi) \sum_{i=1}^N w_i e^{jk_0 \left( x_i sin \theta cos \phi + y_i sin \theta sin \phi + z_i cos \theta \right) } [/math]
In the case of a uniform rectangular array grid with Nx, Ny, Nz elements along the X, Y, Z directions, respectively, and element spacings Sx, Sy, Sz elements along the X, Y, Z directions, respectively, the above expression reduces to the following form:
[math] \mathbf{E_{tot}^{ff}}(\theta,\phi) = \mathbf{E_0^{ff}}(\theta,\phi) \sum_{m=1}^{N_x} \sum_{n=1}^{N_y} \sum_{l=1}^{N_z} w_{ijk} e^{jk_0 \left( (m-1)S_x sin \theta cos \phi + (n-1)S_y sin \theta sin \phi + (l-1)S_z cos \theta \right) } [/math]
The right hand side of the above equation shows the product of the "Element Pattern" by the "Array Factor".
In a phased array antenna system, a uniform phase progression is applied between successive elements along the principal axes. If the phase progression is denoted by ΔΦx, ΔΦy and ΔΦz along the X, Y and Z-axes, respectively, then the far-field expression reduces to:
[math] \mathbf{E_{tot}^{ff}}(\theta,\phi) = \mathbf{E_0^{ff}}(\theta,\phi) \sum_{m=1}^{N_x} \sum_{n=1}^{N_y} \sum_{l=1}^{N_z} w^x_i w^y_j w^z_k e^{j \left[ (m-1)(k_0 S_x sin \theta cos \phi + \Delta\Psi_x ) + (n-1)(k_0 S_y sin \theta sin \phi + \Delta\Psi_y ) + (l-1)(k_0 S_z cos \theta + \Delta\Psi_z ) \right] } [/math]
where wxi, wyj and wzk are real-valued one-dimensional weight distribution sequences along the three principal axes, respectively.
Electromagnetic Scattering and Radar Cross Section
When the physical structure is illuminated by a plane wave source, the calculated far field data indeed represent the scattered fields. In that case, the incident and scattered fields can be separated. The radar cross section (RCS) of a target is defined as follows:
- [math]\sigma_{\theta} = 4\pi r^2 \dfrac{ \big| \mathbf{E}_{\theta}^{scat} \big| ^2} {\big| \mathbf{E}^{inc} \big|^2} [/math]
- [math]\sigma_{\phi} = 4\pi r^2 \dfrac{ \big| \mathbf{E}_{\phi}^{scat} \big| ^2} {\big| \mathbf{E}^{inc} \big|^2} [/math]
- [math]\sigma = \sigma_{\theta} + \sigma_{\phi} = 4\pi r^2 \dfrac{ \big| \mathbf{E}_{tot}^{scat} \big| ^2} {\big| \mathbf{E}^{inc} \big|^2}[/math]
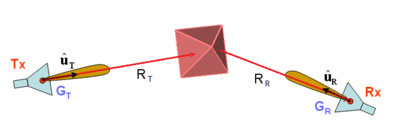
In a bistatic radar system configuration, the transmitting and receiving antennas are different and located at different locations. The radar equations, which related the received power to the transmitted power, can be expressed as:
- [math] P_R = P_T \, G_T G_R \frac{\sigma}{4\pi} \left( \frac{\lambda_0}{4\pi R_T R_R} \right)^2 \left| \mathbf{ \hat{u}_w \cdot \hat{u}_R } \right|^2 [/math]
where uw is the unit polarization vectors of the incoming wave.
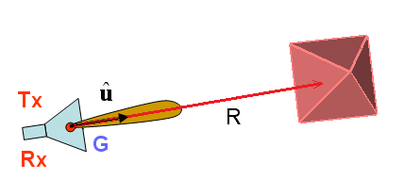
In a mono-static radar system configuration, the same antenna is used as transmitter or receiver using a T/R switch. In that case, GT = GR = G and RT = RR = R. The radar equation is then reduced to:
- [math] P_R = P_T \, \frac{\sigma}{4\pi} \left( \frac{\lambda_0}{4\pi} G \right)^2 \left( \frac{1}{R^4} \right) \left| \mathbf{ \hat{u}_w \cdot \hat{u}_R } \right|^2 [/math]
In other words, the power of the echo signal drops as the fourth power of the distance between the radar and the target.