Difference between revisions of "Using Python to Create Functions, Models & Scripts"

From Emagtech Wiki
Jump to: navigation, search
(→‎EM.Cube's Function Library)
 
(47 intermediate revisions by 2 users not shown)
Line 1: Line 1:
−
[[Image:Splash-generic2.jpg|right|800px]]
+
[[Image:Splash-generic2.jpg|right|720px]]
 
<table>
 
<table>
 
<tr>
 
<tr>
−
<td>[[image:Cube-icon.png | link=Getting_Started_with_EM.CUBE]] [[image:cad-ico.png | link=CubeCAD]] [[image:fdtd-ico.png | link=EM.Tempo]] [[image:prop-ico.png | link=EM.Terrano]] [[image:po-ico.png | link=EM.Illumina]] [[image:static-ico.png | link=EM.Ferma]] [[image:planar-ico.png | link=EM.Picasso]] [[image:metal-ico.png | link=EM.Libera]] </td>
+
<td>[[image:Cube-icon.png | link=Getting_Started_with_EM.Cube]] [[image:cad-ico.png | link=Building Geometrical Constructions in CubeCAD]] [[image:fdtd-ico.png | link=EM.Tempo]] [[image:prop-ico.png | link=EM.Terrano]] [[image:static-ico.png | link=EM.Ferma]] [[image:planar-ico.png | link=EM.Picasso]] [[image:metal-ico.png | link=EM.Libera]] [[image:po-ico.png | link=EM.Illumina]] </td>
 
<tr>
 
<tr>
 
</table>
 
</table>
−
[[Image:Back_icon.png|40px]] '''[[EM.Cube | Back to EM.Cube Main Page]]'''
+
[[Image:Back_icon.png|30px]] '''[[EM.Cube | Back to EM.Cube Main Page]]'''
 +
== Applications of Python Scripting in EM.Cube ==
 +
 
 +
Python is a very powerful and versatile programming language. It can easily be used to create simple functions and scripts. You can use Python in [[EM.Cube]] in a variety of ways:
 +
 
 +
* As an online calculator through [[EM.Cube]]'s command line
 +
* To generate simple mathematical expressions or sophisticated functions involving conditional statements and recursive loops
 +
* To export the geometry of the whole physical structure or parts of it to a Python script and import it later in other projects
 +
* To create wizards that readily reproduce reusable structures 
 +
* To generate computationally simpler surrogate models based on full-wave simulation data
 +
* To write scripts for controlling the simulation flow
 +
 
 
== Working with Mathematical Expressions ==
 
== Working with Mathematical Expressions ==
  
Line 18: Line 29:
 
* Defining custom temporal excitation waveforms in [[EM.Tempo]]
 
* Defining custom temporal excitation waveforms in [[EM.Tempo]]
  
−
Mathematical expressions are indeed text strings made up of reserved names like variable or standard output parameters in combination with operators and functions. You can use the basic arithmetic operators: addition "+", subtraction "-", multiplication "*", division "/", as well as the right and left parentheses "(" and ")" as delimiters. For raising powers, you can either use the power function pow(x,y) or simply use the symbol "**", e.g. "x**y". The Pi number &pi; = 3.1415926... is denoted by "pi" as a reserved name, and letter "e" stands for the Euler number e = 2.7182818... or the base of natural logarithm.
+
Mathematical expressions are indeed text strings made up of reserved names like variable or standard output parameters in combination with operators and functions. You can use the basic arithmetic operators: addition "+", subtraction "-", multiplication "*", division "/", as well as the right and left parentheses "(" and ")" as delimiters. For raising powers, you can either use the power function pow(x,y) or simply use the symbol "**", <i>e.g.</i> "x**y". The Pi number &pi; = 3.1415926... is denoted by "pi" as a reserved name, and letter "e" stands for the Euler number e = 2.7182818... or the base of natural logarithm.
  
 
== EM.Cube's Function Library ==
 
== EM.Cube's Function Library ==
 
      
 
      
−
[[EM.Cube]] provides an extensive library of standard and advanced mathematical functions as well as some special functions related to signal processing and RF design. You can see a list of this functions by clicking the '''Functions''' button [[File:Functions_icon.png]] of the Simulate Toolbar or selecting '''Menu > Simulate > Functions...''' or using the keyboard shortcut {{key|Ctrl+I}}.
+
[[EM.Cube]] provides an extensive library of standard and advanced mathematical functions as well as some special functions related to signal processing and RF design. You can see a list of this functions by clicking the '''Functions''' [[File:Functions_icon.png]] button of the Simulate Toolbar or selecting the menu item '''Simulate &rarr; Functions...''' or using the keyboard shortcut {{key|Ctrl+I}}.
  
 
<table>
 
<table>
 
<tr>
 
<tr>
 
<td>  
 
<td>  
−
[[Image:Variable6.png|thumb|left|540px|EM.Cube's Python functions list.]]
+
[[Image:PY MAN2.png|thumb|left|720px|EM.Cube's Python functions list.]]
 
</td>  
 
</td>  
 
</tr>
 
</tr>
 
</table>
 
</table>
  
−
== Creating Custom Functions Using Models ==
+
[[Image:Info_icon.png|30px]] Click here to learn more about '''[[Glossary of EM.Cube's Python Functions#Standard Python Functions | Python's Standard & Advanced Mathematical Functions]]'''.
  
−
Besides the standard mathematical functions and a large set of library functions, [[EM.Cube]] allows you to create custom functions of your own in a number of ways. User defined functions in [[EM.Cube]] are called "Models". A model is essentially a function of one or more variables defined by way of a "Method" that is saved to an ASCII text file. [[EM.Cube]] currently provides four types of models:
+
== Creating Custom Python Functions ==
  
−
* '''[[#Defining a New Functional Model | Functional Model]]'''
+
Besides the standard mathematical functions and a large set of library functions, [[EM.Cube]] allows you to create custom Python functions of your own. If you are an avid Python programmer, you already know how to write Python function scripts and import the corresponding module using [[EM.Cube]]'s Python command line.
−
* '''[[#Using Data Files to Define Models | Tabular Model]]'''
+
−
* '''[[#Using Python Scripts to Define Models | Python Model]]'''
+
−
* '''[[#Generating HDMR Models | HDMR Model]]'''
+
  
−
A functional model is the simplest type of model and consists of a mathematical expression in terms of one or more arguments or variables. The mathematical expression can involve any combination of the variables, basic operations and standard and library functions. An tabular model takes a data file with X and Y columns and provides a interpolator for the intermediate values. A Python model is a Python script that takes one or more arguments or variables and returns a real value.  
+
For those new to Python programming, [[EM.Cube]] offers a blank Python file, which you can open and modify as a starting point. [[EM.Cube]] provides a list of all the preloaded Python scripts along with your own "user-defined" Python functions in its "Models Dialog". Open [[EM.Cube]]'s Models Dialog by clicking the '''Models''' [[File:Models_icon.png]] button of the Simulate Toolbar or selecting the menu item '''Simulate &rarr; Models...''' or using the keyboard shortcut {{key|Ctrl+L}}. Locate the Python file called "blank.PY" in the list, select and highlight it and click the '''Open''' button of the dialog. The Python file is opened using the text editor you have associated with ".PY" files in Windows. For example, Notepad++ is a powerful and popular choice.  
  
−
An HDMR model is an advanced type of interpolation model that uses the simulation data generated by one of [[EM.Cube]]'s simulation engines. HDMR models are constructed at the end of a special sweep simulation based on the '''High-Dimensional Model Reduction''' (HDMR) method and will be discussed in more detail later.
 
−
 
−
Models can be used anywhere in [[EM.Cube]] just like standard and library functions. They can be used to define dependent variables in the Variables dialog. Or you can use models in expressions that replace the numeric values of object properties in property dialogs.
 
−
 
−
== Defining a New Functional Model ==
 
−
 
−
Follow the procedure below to define a new model in [[EM.Cube]]:
 
−
* Open [[EM.Cube]]'s Models Dialog by clicking the '''Models''' button [[File:Models_icon.png]] of the Simulate Toolbar or selecting '''Menu > Simulate > Models...''' or using the keyboard shortcut {{key|Ctrl+L}}.
 
−
* To add a new model, click the '''Add''' button to open the "Add Model" dialog. Choose one of the three options: Functional, Tabular or Python. Keep in mind that HDMR models are built differently through a special sweep process.
 
−
* In the Model Definition dialog, type in the list of the arguments of your model separated by commas, e.g. x,y,z, ...
 
−
* Choose a name for your new model. This same name will also be given later to a ".DAT" data file associated with your new model. Therefore, choose a unique name for your model that distinct from your project's existing data files.
 
−
* In the case of a functional model, enter the mathematical expression as a function of the arguments you defined earlier.
 
−
 
−
Once you close the model definition dialog, a new entry is added to the Models List. A functional model file with a '''.UDM''' file extension is created in your project's folder. It is recommended that you use the same name for functional models and their model files. The example in the figure below shows a two-variable function called Sinc2D with two arguments x and y. From this point on, you can use your new function Sinc2D(x,y) everywhere in [[EM.Cube]] as you would use any standard or library function. You can always edit a model using the {{key|Edit}} button of the Models dialog. For example, you can change the mathematical expression of a functional model or add new arguments to it.   
 
−
 
−
{{Note|As soon as you define any new model, all of its arguments are added to [[EM.Cube]]'s Variables List as new variables that you can use elsewhere.}}
 
−
 
 
<table>
 
<table>
 
<tr>
 
<tr>
−
<td> [[Image:Variable16.png|thumb|490px|The Models dialog.]] </td>
+
<td>
−
<td> [[Image:Variable17.png|thumb|230px|Choosing the model type.]] </td>
+
[[Image:PY MAN1.png|thumb|left|720px|EM.Cube's models dialog.]]
−
</tr>
+
</td>
−
</table>
+
−
<table>
+
−
<tr>
+
−
<td> [[Image:Variable18.png|thumb|420px|Defining a functional model.]] </td>
+
−
<td> [[Image:Variable15.png|thumb|300px|The contents of the ".UDM" model file.]] </td>
+
 
</tr>
 
</tr>
 
</table>
 
</table>
  
−
== Using Python Scripts to Define Models ==
+
The easiest way of defining a Python function is using the "def" statement. The contents of the blank file are shown below:
  
−
If you have installed the Python scripting language on your computer, you can use Python scripts to define your custom models. In this case, you can build sophisticated models involving conditional statements or recursive loops. If you select the '''Python''' option of the "Add Model" dialog, a new dialog opens up where you can enter your Python script. First you need to define the argument(s) of your model. Then choose a name for your model and its associated model file. A Python script file with a '''.PY''' file extension will be added to your project's folder. In the box labeled '''Python Script''', you can enter your Python code. Make sure that your code contains at lease one "return" statement to generate a value for your custom function. The figure below shows a Python model called MyTestPyModel that has one argument x and calculates the sinc function and returns sin(&pi;x)/(&pi;x). Once your new Python model is added to the Models List, you can use the new function MyTestPyModel(x) everywhere in [[EM.Cube]] just like any standard or library function. You can always edit a Python model using the {{key|Edit}} button of the Models dialog, e.g. you can change the contents of the Python script, add new arguments to the model, or change the returned value.     
 
  
−
<table>
+
-----
−
<tr>
+
 
−
<td> [[Image:Variable19.png|thumb|360px|Defining a Python model.]] </td>
+
 
−
<td> [[Image:Variable20.png|thumb|360px|The contents of the ".PY" model file.]] </td>
+
import sys
−
</tr>
+
 
−
</table>
+
from math import *
 +
 
 +
from emag import *
 +
 
 +
import numpy as np
 +
 
 +
import scipy.special as sp
 +
 
 +
 
 +
def func_name(x):
 +
 
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;#Write your python code here
 +
 
 +
 
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;return x
 +
 
 +
 
 +
-----
 +
 
 +
 
 +
It is recommended that you choose the same name for both your Python function and your Python file. First, save the opened blank file as a new Python file with your new name using Windows' "Save As..." operation. Then, replace "func_name" in the above script with your new name. By default, a single argument "x" is assumed. You can have any arbitrary number of arguments using a comma-separated list. Keep in mind that indentation is very important in Python. You can use either spaces or tabs to create indentation. But you cannot mix them together in the same script. Enter the body of your function in the space provided with the proper indentation. Make sure you return a value for your function. 
 +
 
 +
As an example, the script below shows a new Python function called "MyFunc" save in the Python file "MyFunc.PY":
 +
 
 +
 
 +
-----
 +
 
 +
 
 +
import sys
 +
 
 +
from math import *
 +
 
 +
from emag import *
 +
 
 +
import numpy as np
 +
 
 +
import scipy.special as sp
 +
 
 +
 
 +
def MyFunc(x):
 +
 
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;#Write your python code here
 +
 
 +
&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;&nbsp;return cos(x)-x
 +
 
 +
 
 +
-----
  
−
== What Can You Do with Your Models?==
+
== What Can You Do with Your Python Functions?==
  
−
[[EM.Cube]] models, whether functional, tabular, Python or HDMR, can be used just like any standard or library function in many scenarios:
+
The user defined Python functions can be used just like any standard or library function in many scenarios:
  
−
* For defining a dependent variable in Variables dialog
+
* For defining a dependent variable in variables dialog
 
* For building expressions that can replace the numeric values of object properties
 
* For building expressions that can replace the numeric values of object properties
−
* For defining custom curves or surfaces in Curve Generator and Surface Generator, respectively
+
* For defining custom geometric objects in curve generator or surface generator
 
* For defining custom waveforms for [[EM.Tempo]]'s excitation sources
 
* For defining custom waveforms for [[EM.Tempo]]'s excitation sources
−
* For creating new data in Data Generator
+
* For creating new data in data generator
−
* For performing mathematical operations on data in Data Manager's spreadsheets
+
* For performing mathematical operations on data in data manager's spreadsheets
  
−
In all of the above applications, you instantiate a model using a similar syntax as a regular standard function: "Mode_Name(x,y,…)", where x, y, … are the model's arguments.  
+
In all of the above applications, you instantiate a model using a similar syntax as a regular standard function: "Model_Name(x,y,…)", where x, y, … are the model's arguments.  
  
−
Besides the above applications, you can also access models directly from the Models Dialog. In this dialog, you can select any model and use the {{key|Edit}} button to modify the definition or attributes of the selected model. You can use the Windows '''Notepad''' to open the model file and view its contents. You can also perform three important operations with any model in [[EM.Cube]]:
+
Besides the above applications, you can also perform important operations using Python models such as:
  
 
* Parametric Sweep
 
* Parametric Sweep
 
* Optimization  
 
* Optimization  
−
* HDMR Sweep
+
* Monte Carlo Simulation
  
−
As mentioned earlier, all the arguments of a model are added automatically to the Variables List, and can be used as regular independent variables. You can run a parametric sweep of a model in the same way you run a parametric sweep using any of [[EM.Cube]]'s simulation engines. In this process, successive evaluations of the model are made for all samples of the sweep variable(s). The results are written to an ASCII data file with a '''.DAT''' file extension that bears the same name as your model. To run a parametric sweep of a model, first select it from the Model dialog's list and then click the {{key|Sweep}} button of this dialog. This opens up the Parametric Sweep Settings Dialog, just as you will see in a regular parametric sweep in any of [[EM.Cube]]'s computational modules. Follow the same typical sweep procedure and define your sweep variables from the list of available independent variables, which in this case must be the arguments of your model. At the end of the sweep simulation, open the '''Data Manager''' to view or plot the output data file.  
+
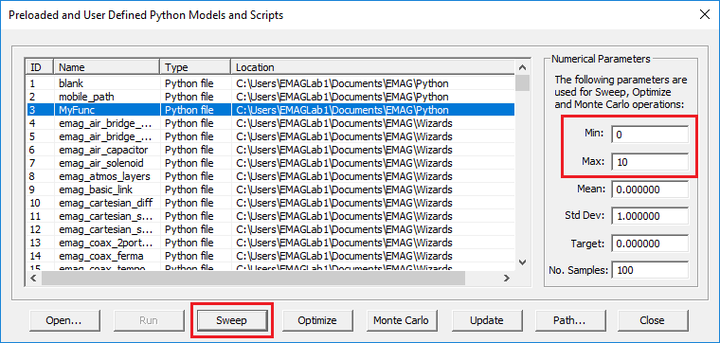
For single-variable Python functions, [[EM.Cube]]'s modes dialog provides an easy way of performing a sweep, optimization of Monte Carlo simulation. Three buttons labeled '''Sweep''', '''Optimize''' and '''Monte Carlo''' are intended for this purpose. In the case of sweep, you must enter '''Min''' and '''Max''' values for the sweep variable as well as '''Number of Samples'''. Select and highlight the name of your Python function from the list and click the '''Sweep''' button to run the sweep. At the completion of the sweep, the sweep data are saved in the file "MyFunc_sweep.DAT". Click the <b>Data Manager</b> [[Image:fdtd_datamanagerb.png]] button of Simulate Toolbar, or use the keyboard shortcut {{key|Ctrl+D}}, or select the menu item '''Simulate &rarr; Data Manager'''. Select the file "MyFunc_sweep.DAT" from the list by clicking on its name and highlighting its row in the table. Click the {{key|Plot}} button of the dialog. A graph of your sweep data is plotted in PyPlot.
−
 
+
−
[[Image:Info_icon.png|40px]] Click here to learn more about '''[[Parametric_Modeling,_Sweep_%26_Optimization#Running_Parametric_Sweep_Simulations_in_EM.Cube | Running Parametric Sweep Simulations]]'''.
+
  
−
In a similar way, you can perform an optimization on your models. In this case you have to define a objective that includes the name of your model (as an output parameter) or any expression of it. You define your objectives in the '''Objectives Dialog'''. To run a optimization of a model, first select it from the Model dialog's list and then click the {{key|Optimize}} button of this dialog. This opens up the Optimization Settings Dialog, just as you will see in a regular optimization in any of [[EM.Cube]]'s computational modules. In this dialog, you need to define your optimization variables from the list of available independent variables, which in this case must be the arguments of your model. Note that your model can have several arguments and you can run a multivariable optimization. At the end of the optimization process, assuming that the optimizer algorithm converges, the current value of the optimization variable in the Variables List will be updated with its computed optimal value. 
+
<table>
 +
<tr>
 +
<td>
 +
[[Image:PY MAN4.png|thumb|left|720px|Running a sweep of "MyFunc(x)" from the models dialog.]]
 +
</td>
 +
</tr>
 +
<tr>
 +
<td>
 +
[[Image:PY MAN5.png|thumb|left|480px|A graph of "MyFunc(x)" plotted in PyPlot.]]
 +
</td>
 +
</tr>
 +
</table>
  
−
[[Image:Info_icon.png|40px]] Click here to learn more about '''[[Parametric_Modeling,_Sweep_%26_Optimization#Optimization | Running Optimization Simulations]]'''.
+
In the case of optimization, you must enter '''Min''' and '''Max''' values for the optimization variable as well as a '''Target''' value for your Python function. Select and highlight the name of your Python function from the list and click the '''Optimize''' button to run the optimization. An objective function of the form e(x) = |func_name(x) - Target| is constructed and minimized. After the optimization algorithms converge, the optimal value of x and the optimization error are reported in the command window.  
  
−
You can also generate an HDMR model from the numerical evaluations of any of your models. To run a HDMR sweep of a model, first select it from the Model dialog's list and then click the {{key|HDMR}} button of this dialog. This opens up the HDMR Settings Dialog, just as you will see in a regular HDMR sweep in most of [[EM.Cube]]'s computational modules. In this way you can create a new compact HDMR model for your model of a different type.
+
<table>
 +
<tr>
 +
<td>
 +
[[Image:PY MAN6.png|thumb|left|480px|The command window showing the results of optimizing "MyFunc(x)" with a target value of 0.5 over the interval [0, 10]. The optimal value is reported to be x = 0.415083.]]
 +
</td>
 +
</tr>
 +
</table>
 +
 
 +
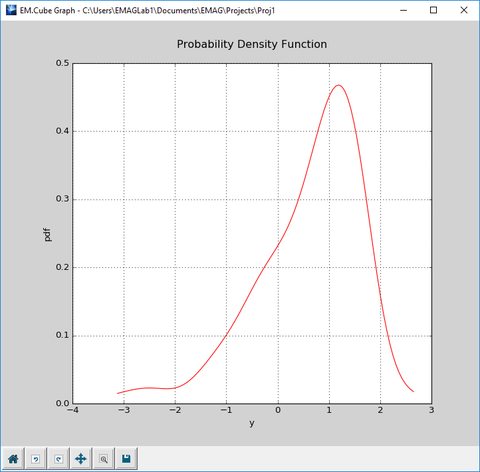
In the case of Monte Carlo simulation, you must enter values for '''Mean''' and '''Std Dev''' of the sweep variable as well as '''Number of Samples'''. Select and highlight the name of your Python function from the list and click the '''Monte Carlo''' button to run the simulation. Through this process, the probability density function (PDF) of your observable y = func_name(x) is estimated, and its graph is plotted as a function of y in PyPlot (file "MyFunc_mc.DAT" from the Data Base list). The mean and standard deviation of y are also reported in the command window.
 +
 
 +
<table>
 +
<tr>
 +
<td>
 +
[[Image:PY MAN7.png|thumb|left|480px|A graph of the estimated probability density function of "MyFunc(x)" with &mu; = 0 and &sigma; = 1.]]
 +
</td>
 +
</tr>
 +
</table>
  
−
[[Image:Info_icon.png|40px]] Click here to learn more about '''[[Running_HDMR_Simulations_in_EM.Cube | Running HDMR Sweep Simulations]]'''.
+
<br />
  
−
{{Note|Running an optimization of your structure using one of [[EM.Cube]]'s simulation engines can be a very time consuming and memory-intensive task. Instead, you may consider developing a model for a certain response or quantity of interest in your structure as a function of one or more structure parameters and then run an optimization of that model far more efficiently.}}
+
<hr>
  
−
<p>&nbsp;</p>
+
[[Image:Top_icon.png|30px]] '''[[#Applications of Python Scripting in EM.Cube | Back to the Top of the Page]]'''
−
[[Image:Top_icon.png|48px]] '''[[#EM.Cube.27s_Function_Library | Back to the Top of the Page]]'''
+
  
−
[[Image:Back_icon.png|40px]] '''[[EM.Cube | Back to EM.Cube Main Page]]'''
+
[[Image:Back_icon.png|30px]] '''[[EM.Cube | Back to EM.Cube Main Page]]'''

Latest revision as of 15:51, 25 June 2018

Splash-generic2.jpg
Cube-icon.png Cad-ico.png Fdtd-ico.png Prop-ico.png Static-ico.png Planar-ico.png Metal-ico.png Po-ico.png

Back icon.png Back to EM.Cube Main Page

Applications of Python Scripting in EM.Cube

Python is a very powerful and versatile programming language. It can easily be used to create simple functions and scripts. You can use Python in EM.Cube in a variety of ways:

  • As an online calculator through EM.Cube's command line
  • To generate simple mathematical expressions or sophisticated functions involving conditional statements and recursive loops
  • To export the geometry of the whole physical structure or parts of it to a Python script and import it later in other projects
  • To create wizards that readily reproduce reusable structures
  • To generate computationally simpler surrogate models based on full-wave simulation data
  • To write scripts for controlling the simulation flow

Working with Mathematical Expressions

Mathematical expressions are widely used throughout EM.Cube for a variety of purposes:

  • Defining dependent variables based on existing independent variables
  • Defining custom output parameters based on standard output parameters
  • Defining design objectives based on standard or custom output parameters
  • Performing operation on and modifying existing data files
  • Generating new data files from the ground up
  • Defining new custom geometric objects using CubeCAD's curve generator and surface generator
  • Defining custom temporal excitation waveforms in EM.Tempo

Mathematical expressions are indeed text strings made up of reserved names like variable or standard output parameters in combination with operators and functions. You can use the basic arithmetic operators: addition "+", subtraction "-", multiplication "*", division "/", as well as the right and left parentheses "(" and ")" as delimiters. For raising powers, you can either use the power function pow(x,y) or simply use the symbol "**", e.g. "x**y". The Pi number π = 3.1415926... is denoted by "pi" as a reserved name, and letter "e" stands for the Euler number e = 2.7182818... or the base of natural logarithm.

EM.Cube's Function Library

EM.Cube provides an extensive library of standard and advanced mathematical functions as well as some special functions related to signal processing and RF design. You can see a list of this functions by clicking the Functions Functions icon.png button of the Simulate Toolbar or selecting the menu item Simulate → Functions... or using the keyboard shortcut Ctrl+I.

EM.Cube's Python functions list.

Info icon.png Click here to learn more about Python's Standard & Advanced Mathematical Functions.

Creating Custom Python Functions

Besides the standard mathematical functions and a large set of library functions, EM.Cube allows you to create custom Python functions of your own. If you are an avid Python programmer, you already know how to write Python function scripts and import the corresponding module using EM.Cube's Python command line.

For those new to Python programming, EM.Cube offers a blank Python file, which you can open and modify as a starting point. EM.Cube provides a list of all the preloaded Python scripts along with your own "user-defined" Python functions in its "Models Dialog". Open EM.Cube's Models Dialog by clicking the Models Models icon.png button of the Simulate Toolbar or selecting the menu item Simulate → Models... or using the keyboard shortcut Ctrl+L. Locate the Python file called "blank.PY" in the list, select and highlight it and click the Open button of the dialog. The Python file is opened using the text editor you have associated with ".PY" files in Windows. For example, Notepad++ is a powerful and popular choice.

EM.Cube's models dialog.

The easiest way of defining a Python function is using the "def" statement. The contents of the blank file are shown below:



import sys

from math import *

from emag import *

import numpy as np

import scipy.special as sp


def func_name(x):

        #Write your python code here


        return x



It is recommended that you choose the same name for both your Python function and your Python file. First, save the opened blank file as a new Python file with your new name using Windows' "Save As..." operation. Then, replace "func_name" in the above script with your new name. By default, a single argument "x" is assumed. You can have any arbitrary number of arguments using a comma-separated list. Keep in mind that indentation is very important in Python. You can use either spaces or tabs to create indentation. But you cannot mix them together in the same script. Enter the body of your function in the space provided with the proper indentation. Make sure you return a value for your function.

As an example, the script below shows a new Python function called "MyFunc" save in the Python file "MyFunc.PY":



import sys

from math import *

from emag import *

import numpy as np

import scipy.special as sp


def MyFunc(x):

        #Write your python code here

        return cos(x)-x


What Can You Do with Your Python Functions?

The user defined Python functions can be used just like any standard or library function in many scenarios:

  • For defining a dependent variable in variables dialog
  • For building expressions that can replace the numeric values of object properties
  • For defining custom geometric objects in curve generator or surface generator
  • For defining custom waveforms for EM.Tempo's excitation sources
  • For creating new data in data generator
  • For performing mathematical operations on data in data manager's spreadsheets

In all of the above applications, you instantiate a model using a similar syntax as a regular standard function: "Model_Name(x,y,…)", where x, y, … are the model's arguments.

Besides the above applications, you can also perform important operations using Python models such as:

  • Parametric Sweep
  • Optimization
  • Monte Carlo Simulation

For single-variable Python functions, EM.Cube's modes dialog provides an easy way of performing a sweep, optimization of Monte Carlo simulation. Three buttons labeled Sweep, Optimize and Monte Carlo are intended for this purpose. In the case of sweep, you must enter Min and Max values for the sweep variable as well as Number of Samples. Select and highlight the name of your Python function from the list and click the Sweep button to run the sweep. At the completion of the sweep, the sweep data are saved in the file "MyFunc_sweep.DAT". Click the Data Manager Fdtd datamanagerb.png button of Simulate Toolbar, or use the keyboard shortcut Ctrl+D, or select the menu item Simulate → Data Manager. Select the file "MyFunc_sweep.DAT" from the list by clicking on its name and highlighting its row in the table. Click the Plot button of the dialog. A graph of your sweep data is plotted in PyPlot.

Running a sweep of "MyFunc(x)" from the models dialog.
A graph of "MyFunc(x)" plotted in PyPlot.

In the case of optimization, you must enter Min and Max values for the optimization variable as well as a Target value for your Python function. Select and highlight the name of your Python function from the list and click the Optimize button to run the optimization. An objective function of the form e(x) = |func_name(x) - Target| is constructed and minimized. After the optimization algorithms converge, the optimal value of x and the optimization error are reported in the command window.

The command window showing the results of optimizing "MyFunc(x)" with a target value of 0.5 over the interval [0, 10]. The optimal value is reported to be x = 0.415083.

In the case of Monte Carlo simulation, you must enter values for Mean and Std Dev of the sweep variable as well as Number of Samples. Select and highlight the name of your Python function from the list and click the Monte Carlo button to run the simulation. Through this process, the probability density function (PDF) of your observable y = func_name(x) is estimated, and its graph is plotted as a function of y in PyPlot (file "MyFunc_mc.DAT" from the Data Base list). The mean and standard deviation of y are also reported in the command window.

A graph of the estimated probability density function of "MyFunc(x)" with μ = 0 and σ = 1.


Top icon.png Back to the Top of the Page

Back icon.png Back to EM.Cube Main Page

Retrieved from "http://www.emagtech.com/wiki/index.php?title=Using_Python_to_Create_Functions,_Models_%26_Scripts&oldid=38273"