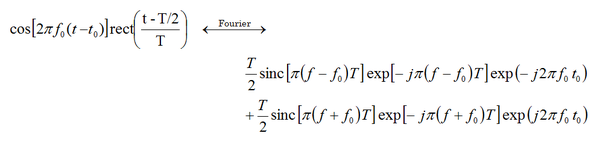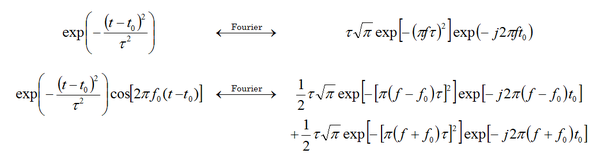A Review of Maxwell's Equations & Computational Electromagnetics (CEM)

Back to EM.Cube Main Page

Maxwell's Equations in Differential Form

Maxwell's equations form the basis for the mathematical formulation of almost all electromagnetic modeling problems. The differential form of Maxwell's equations relates the electric and magnetic fields and sources locally at every point in the space. In an isotropic, time-invariant and homogeneous medium, they are given by:

[math] \nabla . \mathbf{D} = \rho [/math]

[math] \nabla . \mathbf{B} = 0 [/math]

[math] \nabla \times \mathbf{E} = - \dfrac{\partial \mathbf{B}}{\partial t} [/math]

[math] \nabla \times \mathbf{H} = \dfrac{\partial \mathbf{D}}{\partial t} + \mathbf{J} [/math]

where ∇ is the gradient operator:

[math] \nabla = \dfrac{\partial}{\partial x}\hat{\mathbf{x}} + \dfrac{\partial}{\partial y}\hat{\mathbf{y}} + \dfrac{\partial}{\partial z}\hat{\mathbf{z}} [/math]

∇. denotes the divergence operation, ∇× denotes the curl operation, E and H are the electric and magnetic fields in V/m and A/m, respectively, D and B are the electric and magnetic flux densities in C/m² and Wb, respectively, J is the electric volume current density in A/m², ρ is the electric volume charge density in C//m³, and the following constitutive relationships hold:

[math] \mathbf{D} = \epsilon \mathbf{E}, \quad \quad \mathbf{B} = \mu \mathbf{H}, \quad \quad \mathbf{J} = \sigma \mathbf{E} [/math]

where ε is the permittivity in F/m, μ is the permeability in H/m, and σ is the electric conductivity of the medium in S/m.

Although real magnetic charges and currents do not exist in nature, using the electromagnetic equivalence theorem, it is convenient to introduce a magnetic volume charge density in C/m³, and a magnetic volume current density M in V/m² to preserve the symmetry and duality of Maxwell's equations in the following form:

[math] \nabla . \mathbf{D} = \rho [/math]

[math] \nabla . \mathbf{B} = \rho_m [/math]

[math] \nabla \times \mathbf{E} = - \dfrac{\partial \mathbf{B}}{\partial t} - \mathbf{M} [/math]

[math] \nabla \times \mathbf{H} = \dfrac{\partial \mathbf{D}}{\partial t} + \mathbf{J} [/math]

The following constitutive relationships now hold:

[math] \mathbf{D} = \epsilon \mathbf{E}, \quad \quad \mathbf{J} = \sigma \mathbf{E} [/math]

[math] \mathbf{B} = \mu \mathbf{H}, \quad \quad \mathbf{M} = \sigma_m \mathbf{H} [/math]

where σ_m is the magnetic conductivity of the medium in Ω/m.

Additionally, one can write the following continuity equations:

[math] \nabla . \mathbf{J} - \dfrac{\partial \rho}{\partial t} = 0 [/math]

[math] \nabla . \mathbf{M} - \dfrac{\partial \rho_m}{\partial t} = 0 [/math]

Click here to learn more about EM.Cube's Materials & Physical Object Types.

The Wave Equations

Combining Maxwell's equations, we can arrive at the electric and magnetic wave equations:

[math] \nabla^2 \mathbf{E} - \epsilon \mu \dfrac{\partial \mathbf{E}}{\partial t} = 0 [/math]

[math] \nabla^2 \mathbf{H} - \epsilon \mu \dfrac{\partial \mathbf{H}}{\partial t} = 0 [/math]

where ∇² is the Laplacian operator. The wave equations are hyperbolic partial differential equation in space coordinates and time, which must be solved subject to the proper initial and boundary conditions.

Electric & Magnetic Boundary Conditions

The electric field boundary conditions at the interface between two material media are:

[math] \hat{\mathbf{n}} . [ \mathbf{D_2(r)} - \mathbf{D_1(r)} ] = \rho_s (\mathbf{r}) [/math]

[math] \hat{\mathbf{n}} \times [ \mathbf{E_2(r)} - \mathbf{E_1(r)} ] = - \mathbf{M_s(r)} [/math]

where [math]\hat{\mathbf{n}}[/math] is the unit normal vector at the interface pointing from medium 1 towards medium 2, and ρ_s is the electric surface charge density, and M_s is the magnetic surface current density at the interface.

The magnetic field boundary conditions at the interface between two material media are:

[math] \hat{\mathbf{n}} . [ \mathbf{B_2(r)} - \mathbf{B_1(r)} ] = \rho_{ms} (\mathbf{r}) [/math]

[math] \hat{\mathbf{n}} \times [ \mathbf{H_2(r)} - \mathbf{H_1(r)} ] = \mathbf{J_s(r)} [/math]

where [math]\hat{\mathbf{n}}[/math] is the unit normal vector at the interface pointing from medium 1 towards medium 2, ρ_ms is the magnetic surface charge density, and J_s is the electric surface current density at the interface.

The interface between two material media and definition of unit normal vector.

Maxwell's Equations in Integral Form

In certain applications, it is advantageous to cast Maxwell's equations in an integral form. These can be done using the theorems of vector calculus. In an isotropic, time-invariant and homogeneous medium, the integral forms of Maxwell's equations are given by:

[math] \int\int_S \mathbf{D} . \mathbf{ds} = \int\int\int_V \rho dv [/math]

[math] \int\int_S \mathbf{B} . \mathbf{ds} = \int\int\int_V \rho_m dv [/math]

[math] \int_C \mathbf{E} . \mathbf{dl} = - \dfrac{\partial}{\partial t} \int\int_S \mathbf{B} . \mathbf{ds} - \int\int_S \mathbf{M} . \mathbf{ds} [/math]

[math] \int_C \mathbf{H} . \mathbf{dl} = \dfrac{\partial}{\partial t} \int\int_S \mathbf{D} . \mathbf{ds} - \int\int_S \mathbf{J} . \mathbf{ds} [/math]

where V is a closed region of the space, S the surface boundary and C is a path.

Time-Harmonic Form of Maxwell's Equations

In a time-harmonic system operating at a given frequency f, the time dependence of the fields takes the form of [math] e^{j\omega t} [/math], where [math] j = \sqrt{-1} [/math], and ω = 2πf is the angular frequency. In that case, the time derivative is [math] {\partial}/{\partial t} = j\omega [/math], and Maxwell's curl equations reduce to:

[math] \nabla \times \mathbf{E} = - j\omega \mathbf{B} - \mathbf{M} [/math]

[math] \nabla \times \mathbf{H} = j\omega \mathbf{D} + \mathbf{J} [/math]

and the continuity equations reduce to:

[math] \nabla . \mathbf{J} = j\omega \rho [/math]

[math] \nabla . \mathbf{M} = j\omega \rho_m [/math]

The wave equations then reduce to the Helmholtz equations given by:

[math] \nabla^2 \mathbf{E} + k^2 \mathbf{E} = 0 [/math]

[math] \nabla^2 \mathbf{H} + k^2 \mathbf{H} = 0 [/math]

where [math] k = \omega \sqrt{\epsilon \mu} [/math] is the propagation constant in the medium.

Electric and Magnetic Potentials

Under the time-harmonic assumption, the electric and magnetic fields can further be expressed in terms of an electric scalar potential Φ, a magnetic scalar potential Ψ, a vector electric potential F and a vector magnetic potential A in the following form:

[math] \mathbf{E(r)} = - \nabla \times \mathbf{F(r)} - \nabla \Phi(\mathbf{r}) - j\omega\mu \mathbf{A(r)} [/math]

[math] \mathbf{H(r)} = \nabla \times \mathbf{A(r)} - \nabla \Psi(\mathbf{r}) - j\omega\epsilon \mathbf{F(r)} [/math]

with the additional gauge relations:

[math] \nabla \times \mathbf{A(r)} = - j\omega\epsilon \Phi(\mathbf{r}) [/math]

[math] \nabla \times \mathbf{F(r)} = - j\omega\mu \Psi(\mathbf{r}) [/math]

All the potential functions satisfy the Helmholtz equation:

[math] \nabla^2 \mathbf{A} + k^2 \mathbf{A} = - \mathbf{J} [/math]

[math] \nabla^2 \mathbf{F} + k^2 \mathbf{F} = - \mathbf{M} [/math]

[math] \nabla^2 \Phi + k^2 \Phi = - \frac{\rho}{\epsilon} [/math]

[math] \nabla^2 \Psi + k^2 \Psi = - \frac{\rho_m}{\mu} [/math]

Sometimes it is useful to define the Hertz vector potentials as:

[math] \mathbf{\Pi_e} = \frac{1}{j\omega\epsilon} \mathbf{A(r)} [/math]

[math] \mathbf{\Pi_m} = \frac{1}{j\omega\mu} \mathbf{F(r)} [/math]

In that case, the electric and magnetic fields can be fully expressed in terms of these two vector potentials:

[math] \mathbf{E(r)} = -j\omega\mu \nabla \times \mathbf{\Pi_m} + k^2 \mathbf{\Pi_e} + \nabla \nabla . \mathbf{\Pi_e} [/math]

[math] \mathbf{H(r)} = j\omega\epsilon\nabla \times \mathbf{\Pi_e} + k^2 \mathbf{\Pi_m} + \nabla \nabla . \mathbf{\Pi_m} [/math]

For historical reasons, it is customary in electrostatic problems to directly set the magnetic flux density B equal to ∇ × A. EM.Cube's Static Module (EM.Ferma) uses that convention for definition of the vector magnetic potential A, which is different by a factor of μ from the definition of the A vector in the electrodynamic discussion presented in this section. That would also change the source term of the Helmholtz equation by the same factor.

Green’s Function Representations

The Green’s functions are the analytical solutions of boundary value problems when they are excited by an elementary source. This is usually an infinitesimally small vectorial point source. The total electric (E) field and total magnetic (H) field can be expressed in terms of the volume electric current source J and volume magnetic current source M in the following way:

[math] \mathbf{E = E^{inc}} + \mathbf{\iiint_{V_J} \overline{\overline{G}}_{EJ}(r|r') \cdot J(r') } d \nu' + \mathbf{\iiint_{V_M} \overline{\overline{G}}_{EM}(r|r') \cdot M(r') } d \nu' [/math]

[math] \mathbf{H = H^{inc}} + \mathbf{\iiint_{V_J} \overline{\overline{G}}_{HJ}(r|r') \cdot J(r') } d \nu' + \mathbf{\iiint_{V_M} \overline{\overline{G}}_{HM}(r|r') \cdot M(r') } d \nu' [/math]

where E^inc and H^inc are the incident electric and magnetic fields, respectively, and V_J and V_M are the volumes containing the electric and magnetic current sources, respectively. The above equations involve four dyadic Green's functions types: dyadic electric-field Green’s functions due to electric current sources G_EJ, dyadic magnetic-field Green’s functions due to electric current sources G_HJ, dyadic electric-field Green’s functions due to magnetic current sources G_EM, and dyadic magnetic-field Green’s functions due to magnetic current sources G_HM . The incident or impressed fields represent the source terms and provide the excitation of the structure.

In order for the Green’s functions to be computationally useful, they must have analytical closed forms. This can be a mathematical expression or a more complex recursive process. It is no surprise that only very few electromagnetic boundary value problems have closed-form Green’s functions. Among EM.Cube's computational modules, EM.Libera is based on the free-space Green's functions, whereas EM.Picasso is based on the dyadic Green's functions of an arbitrary multilayer planar structure.

Free-Space Field Solutions

The simplest background structure is the unbounded free space, which is represented by the following Green’s function:

[math] \mathbf{ \overline{\overline{G}}_{EJ}(r|r') = (\overline{\overline{I}} + \nabla\nabla) } G_{\Lambda} (\mathbf{r|r'}), \quad G_{\Lambda} (\mathbf{r|r'}) = \frac{ e^{-jk_0 \mathbf{|r-r'|}} }{ 4\pi \mathbf{|r-r'|} } [/math]

where [math]\mathbf{\overline{\overline{I}}}[/math] is the unit dyad, [math]\nabla[/math] is the gradient operator, r and r' are the position vectors of the observation and source points, respectively, and k₀ is the free-space propagation constant. This implies that electromagnetic waves propagate in free space in a spherical form away from the source. Note that the Green’s function has a singularity at the source, i.e. when r = r'.

Assuming electric and magnetic surface current sources J and M residing on surfaces S_J and S_M, respectively, the near-field equations reduce to:

[math] \begin{align} \mathbf{ E(r) = E^{inc}(r) } & - jk_0 Z_0 \iint_{S_J} \left\{ \left[ 1 - \frac{j}{k_0 R} - \frac{1}{(k_0 R)^2} \right] \mathbf{J(r')} - \left[ 1 - \frac{3j}{k_0 R} - \frac{3}{(k_0 R)^2} \right] \mathbf{ (\hat{R} \cdot J(r')) \hat{R} } \right\} \frac{e^{-jk_0 R}}{4\pi R} ds' \\ & + jk_0 \iint_{S_M} \left[ 1-\frac{j}{k_0 R} \right] \mathbf{ (\hat{R} \times M(r')) } \frac{e^{-jk_0 R}}{4\pi R} ds' \end{align} [/math]

[math] \begin{align} \mathbf{ H(r) = H^{inc}(r) } & - jk_0 Y_0 \iint_{S_M} \left\{ \left[ 1 - \frac{j}{k_0 R} - \frac{1}{(k_0 R)^2} \right] \mathbf{M(r')} - \left[ 1 - \frac{3j}{k_0 R} - \frac{3}{(k_0 R)^2} \right] \mathbf{ (\hat{R} \cdot M(r')) \hat{R} } \right\} \frac{e^{-jk_0 R}}{4\pi R} ds' \\ & - jk_0 \iint_{S_J} \left[ 1-\frac{j}{k_0 R} \right] \mathbf{ (\hat{R} \times J(r')) } \frac{e^{-jk_0 R}}{4\pi R} ds' \end{align} [/math]

where [math] R=|r-r'| \text{, } k_0 = \frac{2\pi}{\lambda_0} \text{ and } Z_0 = 1/Y_0 = \eta_0 [/math].

Definition of the Far Radiation Zone

In general, by far fields we mean the electric fields evaluated in the far zone of a physical structure, which satisfies the following condition:

[math]r \lt\lt \frac{2D^2}{\lambda_0}[/math]

where r is the distance between the observation and source points, λ₀ is the free space wavelength and D is the largest dimension of the radiating structure. In EM.Cube, the far-zone electric fields E^ff(θ, φ) are functions of the spherical observation angles only and are defined as

[math] \begin{align} & \mathbf{E(r) = E} (r,\theta,\phi) = \frac{e^{-jk_0 r}}{r} \mathbf{E^{ff}}(\theta,\phi) \\ & \mathbf{H(r) = H} (r,\theta,\phi) = \frac{1}{\eta_0} \mathbf{ \hat{r} \times E^{ff}(r) } \end{align} \quad k_0 r \gt\gt 1 [/math]

where k₀ = 2π/λ₀ and η₀ = 120π Ω is the intrinsic impedance of the free space.

Computing the Far-Zone Fields from Near-Zone Data

EM.Tempo's FDTD engine calculates the far fields using a near-field-to-far-field transformation of the field quantities on a given closed surface, which is denoted the radiation box. You can use EM.Cube's default radiation box or define your own. EM.Picasso, EM.Libera and EM.Illumina compute the far fields directly by integrating the electric and magnetic surface current solutions to the numerical problem. The far-zone electric field can be written as:

[math] \mathbf{E^{ff}(r)} = \frac{jk_0 e^{-jk_0 r}}{4\pi r} \left\{ \eta_0 \mathbf{ \hat{r} \times \hat{r} } \times \iint_{S_J} \mathbf{J(r')} e^{jk_0 \mathbf{\hat{r}\cdot r'}} ds' + \mathbf{\hat{r}} \times \iint_{S_M} \mathbf{M(r')} e^{jk_0 \mathbf{ \hat{r} \cdot r' } } ds' \right\} [/math]

where J and M are either the actual electric and magnetic surface currents on the surface of your physical structure, or the equivalent electric and magnetic surface currents on the surface of the enclosing radiation box. One can define a pair of electric and magnetic radiation integrals:

[math] \begin{align} & \mathbf{N(r)} = \iint_S \mathbf{J(r')} e^{ jk_0 \mathbf{\hat{r} \cdot r'} } \, ds' \\ & \mathbf{L(r)} = \iint_S \mathbf{M(r')} e^{ jk_0 \mathbf{\hat{r} \cdot r'} } \, ds' \\ \end{align} [/math]

where

[math] \mathbf{\hat{r}} = \sin\theta \cos\phi \mathbf{\hat{x}} + \sin\theta \sin\phi \mathbf{\hat{y}} + \cos\theta \mathbf{\hat{z}} [/math]

In that case, the θ and φ components of the far fields can be computed from the following relationships:

[math] \begin{align} & E_{\theta}^{ff}(\theta, \phi) = -\frac{jk_0}{4\pi} (L_{\phi} + \eta_0 N_{\theta}) \\ & E_{\phi}^{ff}(\theta, \phi) = \frac{jk_0}{4\pi} (L_{\theta} + \eta_0 N_{\phi}) \end{align} [/math]

where the θ and φ components of the radiation integrals are given by:

[math] \begin{align} & N_{\theta}(\theta,\phi) = \iint_S [J_x\cos\theta\cos\phi + J_y\cos\theta\sin\phi - J_z\sin\theta] e^{ jk_0 \mathbf{\hat{r} \cdot r'} } \, ds' \\ & N_{\phi}(\theta,\phi) = \iint_S [-J_x \sin\phi + J_y\cos\phi] e^{ jk_0 \mathbf{\hat{r} \cdot r'} } \, ds' \end{align} [/math]

[math] \begin{align} & L_{\theta}(\theta,\phi) = \iint_S [M_x\cos\theta\cos\phi + M_y\cos\theta\sin\phi - M_z\sin\theta] e^{ jk_0 \mathbf{\hat{r} \cdot r'} } \, ds' \\ & L_{\phi}(\theta,\phi) = \iint_S [-M_x \sin\phi + M_y\cos\phi] e^{ jk_0 \mathbf{\hat{r} \cdot r'} } \, ds' \end{align} [/math]

Radiated Power & Directivity

In calculating the far field quantities, using Poynting's theorem, one can define the radiated power density as:

[math] \mathbf{W} = \frac{1}{2} \text{Re}(\mathbf{E \times H^*}) = \frac{\mathbf{\hat{k}}}{2\eta_0} |\mathbf{E}(r,\theta,\phi)|^2 \, |_{r \to \infty} [/math]

To eliminate the dependency on r, a normalized quantity called "Radiation Intensity" in the following way:

[math] S(\theta,\phi) = \lim_{r \to \infty} r^2 |\mathbf{W}| = \frac{1}{2\eta_0} | \mathbf{E^{ff}}(\theta,\phi)|^2 [/math]

The total radiated power can now be calculated as:

[math] P_{rad} = \int\limits_0^{2\pi} d\phi \int\limits_0^{\pi} d\theta \, S(\theta,\phi) \sin\theta = \frac{1}{2\eta_0} \int\limits_0^{2\pi} \int\limits_0^{\pi} |\mathbf{E^{ff}}(\theta,\phi)|^2 \sin\theta \, d\theta \, d\phi [/math]

The (maximum) Directivity of the radiating structure is calculated using the definition:

[math] D_0 = \frac{4\pi [S(\theta,\phi)]_{max}}{P_{rad}} = \frac{ 4\pi \big| \mathbf{E^{ff}}(\theta,\phi) \big|^2 |_{max} } { \int\limits_0^{2\pi} \int\limits_0^{\pi} \big| \mathbf{E^{ff}}(\theta,\phi) \big|^2 \sin\theta \,d\theta \,d\phi } [/math]

Array Factor

Consider an antenna structure whose radiation center is situated at the origin of the spherical coordinate system (0, 0, 0) and has a far-zone electric field E₀^ff(θ, φ). If you translate this structure to a new arbitrary point (x_i, y_i, z_i), its far field is transformed in the following way:

[math] \mathbf{E_i^{ff}}(\theta,\phi) = \mathbf{E_0^{ff}}(\theta,\phi) e^{jk_0 \left( x_i sin \theta cos \phi + y_i sin \theta sin \phi + z_i cos \theta \right) } [/math]

In the most general sense, an antenna array consists of a set of N identical radiating elements located at coordinates (x_i, y_i, z_i) and excited with complex weight coefficients w_i. Using the principle of linear superposition, the far-zone electro field of the overall antenna array can be expressed as:

[math] \mathbf{E_{tot}^{ff}}(\theta,\phi) = \mathbf{E_0^{ff}}(\theta,\phi) \sum_{i=1}^N w_i e^{jk_0 \left( x_i sin \theta cos \phi + y_i sin \theta sin \phi + z_i cos \theta \right) } [/math]

In the case of a uniform rectangular array grid with N_x, N_y, N_z elements along the X, Y, Z directions, respectively, and element spacings S_x, S_y, S_z elements along the X, Y, Z directions, respectively, the above expression reduces to the following form:

[math] \mathbf{E_{tot}^{ff}}(\theta,\phi) = \mathbf{E_0^{ff}}(\theta,\phi) \sum_{m=1}^{N_x} \sum_{n=1}^{N_y} \sum_{l=1}^{N_z} w_{ijk} e^{jk_0 \left( (m-1)S_x sin \theta cos \phi + (n-1)S_y sin \theta sin \phi + (l-1)S_z cos \theta \right) } [/math]

The right hand side of the above equation shows the product of the "Element Pattern" by the "Array Factor".

Radar Cross Section

When the physical structure is illuminated by a plane wave source, the calculated far field data indeed represent the scattered fields. In that case, the incident and scattered fields can be separated. The radar cross section (RCS) of a target is defined as follows:

[math]\sigma_{\theta} = 4\pi r^2 \dfrac{ \big| \mathbf{E}_{\theta}^{scat} \big| ^2} {\big| \mathbf{E}^{inc} \big|^2}, \quad \sigma_{\phi} = 4\pi r^2 \dfrac{ \big| \mathbf{E}_{\phi}^{scat} \big| ^2} {\big| \mathbf{E}^{inc} \big|^2}, \quad \sigma = \sigma_{\theta} + \sigma_{\phi} = 4\pi r^2 \dfrac{ \big| \mathbf{E}_{tot}^{scat} \big| ^2} {\big| \mathbf{E}^{inc} \big|^2}[/math]

In a bistatic radar system configuration, the transmitting and receiving antennas are different and located at different locations. The radar equations, which related the received power to the transmitted power, can be expressed as:

[math] P_R = P_T \, G_T G_R \frac{\sigma}{4\pi} \left( \frac{\lambda_0}{4\pi R_T R_R} \right)^2 \left| \mathbf{ \hat{u}_w \cdot \hat{u}_R } \right|^2 [/math]

where u_w is the unit polarization vectors of the incoming wave.

In a mono-static radar system configuration, the same antenna is used as transmitter or receiver using a T/R switch. In that case, G_T = G_R = G and R_T = R_R = R. The radar equation is then reduced to:

[math] P_R = P_T \, \frac{\sigma}{4\pi} \left( \frac{\lambda_0}{4\pi} G \right)^2 \left( \frac{1}{R^4} \right) \left| \mathbf{ \hat{u}_w \cdot \hat{u}_R } \right|^2 [/math]

In other words, the power of the echo signal drops as the fourth power of the distance between the radar and the target.

A bistatic radar system configuration.

A monostatic radar system configuration.

Differential Form of Maxwell's Equations & the Yee Cell

Maxwell’s equations for an isotropic, time-invariant and homogeneous medium are given by:

[math] \nabla \times \mathbf{E} = - \dfrac{\partial \mathbf{B}}{\partial t} - \mathbf{M} [/math]

[math] \nabla \times \mathbf{H} = \dfrac{\partial \mathbf{D}}{\partial t} + \mathbf{J} [/math]

where E and H are the electric and magnetic fields, respectively, D and B are the electric and magnetic flux densities, respectively, J and M are the volume electric and magnetic current densities, respectively, and the following constitutive relationships hold:

[math] \mathbf{D} = \epsilon \mathbf{E}, \quad \quad \mathbf{J} = \sigma \mathbf{E} [/math]

[math] \mathbf{B} = \epsilon \mathbf{H}, \quad \quad \mathbf{M} = \sigma_m \mathbf{H} [/math]

where ε is the permittivity, μ is the permeability, σ is the electric conductivity, and σ_m is the magnetic conductivity of the medium.

In a medium without electric or magnetic losses these equations can be rewritten as:

[math]\dfrac{\partial \mathbf{H}}{\partial t} = -\dfrac{1}{\mu} \nabla \times \mathbf{E}[/math]

[math]\dfrac{\partial \mathbf{E}}{\partial t} = \dfrac{1}{\epsilon} \nabla \times \mathbf{H}[/math]

The Yee cell geometry and definition of the electric and magnetic field components.

In the FDTD method, both time- and space-derivatives are approximated with central finite differences. This results in six differential equations, one for each field component, on a Yee cell define at a point in the 3D space as shown in the figure on the right:

[math] H_x^{n+\frac{1}{2}} (i,j,k) = H_x^{n-\frac{1}{2}} (i,j,k) + \frac{\Delta t}{\mu (i,j,k)} \left[ \frac{E_{y}^{n}(i,j,k+1) - E_{y}^{n}(i,j,k)}{\Delta z} - \frac{E_{z}^{n} (i,j+1,k)-E_{z}^{n} (i,j,k)}{\Delta y} \right] [/math]

[math] H_y^{n+\frac{1}{2}} (i,j,k) = H_y^{n-\frac{1}{2}} (i,j,k) + \frac{\Delta t}{\mu (i,j,k)} \left[ \frac{E_{z}^{n}(i+1,j,k) - E_{z}^{n}(i,j,k)}{\Delta x} - \frac{E_{x}^{n} (i,j,k+1)-E_{x}^{n} (i,j,k)}{\Delta z} \right] [/math]

[math] H_z^{n+\frac{1}{2}} (i,j,k) = H_z^{n-\frac{1}{2}} (i,j,k) + \frac{\Delta t}{\mu (i,j,k)} \left[ \frac{E_{x}^{n}(i,j+1,k) - E_{x}^{n}(i,j,k)}{\Delta y} - \frac{E_{y}^{n} (i+1,j,k)-E_{y}^{n} (i,j,k)}{\Delta x} \right] [/math]

[math] {E_{x}^{n+1} (i,j,k) = E_{x}^{n} (i,j,k)} + \frac{\Delta t}{\epsilon (i,j,k)} \left[ \frac{H_{z}^{n+\frac{1}{2} } (i,j,k) - H_{z}^{n+\frac{1}{2} } (i,j-1,k)}{\Delta y} - \frac{H_{y}^{n+\frac{1}{2} } (i,j,k) - H_{y}^{n+\frac{1}{2} } (i,j,k-1)}{\Delta z} \right] [/math]

[math] {E_{y}^{n+1} (i,j,k) = E_{y}^{n} (i,j,k)} + \frac{\Delta t}{\epsilon (i,j,k)} \left[ \frac{H_{x}^{n+\frac{1}{2} } (i,j,k) - H_{x}^{n+\frac{1}{2} } (i,j,k-1)}{\Delta z} - \frac{H_{z}^{n+\frac{1}{2} } (i,j,k) - H_{z}^{n+\frac{1}{2} } (i-1,j,k)}{\Delta x} \right] [/math]

[math] {E_{z}^{n+1} (i,j,k) = E_{z}^{n} (i,j,k)} + \frac{\Delta t}{\epsilon (i,j,k)} \left[ \frac{H_{y}^{n+\frac{1}{2} } (i,j,k) - H_{y}^{n+\frac{1}{2} } (i-1,j,k)}{\Delta x} - \frac{H_{x}^{n+\frac{1}{2} } (i,j,k) - H_{x}^{n+\frac{1}{2} } (i,j-1,k)}{\Delta y} \right] [/math]

where i, j, k are the grid position indices along the X, Y, Z axes, respectively, n is the current time step index and Δx, Δy, Δz are the grid position indices along the X, Y, Z axes, respectively. Similar expressions are obtained for the Y and Z components of the electric and magnetic fields. When your physical structure involves lossy materials with nonzero electric conductivity σ and/or nonzero electric conductivity σ_m, the above update equations become more complicated. In the case of anisotropic materials with tensorial constitutive parameters, the electric displacement vector D and magnetic induction vector B need to be involved in the update of Maxwell's equations at every time step. This results in a total of twelve update equations at every time step. In the case of dispersive materials with time-varying constitutive parameters, additional auxiliary differential equations are invoked and updated at every time step. Applying the proper boundary conditions for all the materials inside the computational domain and at the boundaries of the domain itself, EM.Cube calculates and "updates" all the necessary field components at every mesh node, at every time step.

Why Does FDTD Need Domain Termination?

The FDTD simulation time depends directly on the size of the computational domain. For free space radiation or scattering problems, the computational domain must be extended to infinity, which means an infinite number of cells in the computational domain. The solution to this problem is to truncate the domain by a set of artificial boundaries at a certain distance from the objects in the computational domain. The absorbing boundaries should be such that the field propagates through them without any back reflection. Different methods have been used to simulate an absorbing boundary condition in FDTD simulations. The most common ones are Mur, Liao, and the perfectly match layer (PML). The Mur boundary condition calculates the boundary field values from the three dimensional scalar wave equations, while the Liao boundary condition is based on extrapolation of the fields in space and time. In 1994, Berenger proposed a new boundary condition called the perfectly matched layer (PML), which provides a much better performance than the Liao and Mur boundary conditions. The PML medium properties surrounding the computational domain are chosen to effectively absorb all the outgoing waves propagating towards the boundaries. In PML regions, an artificial conductivity is introduced such that it starts with very small values at the free space-PML interfaces and gradually increases until it reaches its maximum value at the last layer of the PML region.

CPML vs. PML

The PML boundary condition is not effective in absorbing evanescent waves, and it suffers from late-time reflections when simulating fields with very long time signatures. This is partly due to the weakly causal nature of the PML. A strictly causal form of the PML, known as the complex frequency-shifted PML (CFS-PML), was later developed by simply shifting the frequency dependent pole off the real axis and into the negative-imaginary half of the complex plane. It has been shown that the CFS-PML is highly effective at absorbing evanescent waves and signals with a long time signature. Therefore, using the CFS-PML, the boundaries can be placed closer to the objects in the computational domain, and considerable time and memory savings can be achieved. The convolutional PML (CPML) is an efficient implementation of the CFS-PML based on a stretched coordinate formulation in conjunction with recursive convolution. It has been shown that CPML requires only two auxiliary variables per discrete field point and absorbs waves in isotropic, homogeneous, inhomogeneous, lossy, dispersive, anisotropic or non-linear media without any further generalization.

The boundary CPML cells placed outside the visible domain box.

The CPML Formulation

The CPML is formulated in the stretched coordinate space. The CPML layers are assumed to terminate the FDTD computational domain. The X components of Maxwell's frequency-domain curl equations can then be written in the following form:

[math] (j\omega\epsilon_x + \sigma_{ex})\tilde{E}_x = \frac{1}{s_{ey}} \frac{\partial \tilde{H}_z}{\partial y} - \frac{1}{s_{ez}} \frac{\partial \tilde{H}_y}{\partial z} [/math]

[math] (j\omega\mu_x + \sigma_{mx}) \tilde{H}_x = -\frac{1}{s_{my}} \frac{\partial \tilde{E}_z}{\partial y} + \frac{1}{s_{mz}} \frac{\partial \tilde{E}_y}{\partial z} [/math]

where s_ei and s_mi are the stretched coordinate metrics defined by:

[math] s_{ei} = \kappa_{ei} + \frac{\sigma_{ei}}{\alpha_{ei} + j\omega\varepsilon_0}, \quad i=x,y,z [/math]

[math] s_{mi} = \kappa_{mi} + \frac{\sigma_{mi}}{\alpha_{mi} + j\omega\mu_0}, \quad i=x,y,z [/math]

s_ei and s_mi are the anisotropic components of the synthesized electric and magnetic conductivities in the CPML region. κ_ei , κ_mi, α_ei and α_mi are all assumed to be positive real and κ_ei, κ_mi ≥ 1. Similar equations hold for the Y and Z components of the electric and magnetic fields in the CPML layers. The requirement for zero reflection at PML-PML interfaces imposes the following condition:

[math] s_{ei} = s_{mi} \quad \Rightarrow \quad \kappa_{ei} = \kappa_{mi} ,\quad \frac{\sigma_{ei}}{\varepsilon_0} = \frac{\sigma _{mi}}{\mu_0}, \quad \frac{\alpha_{ei}}{\varepsilon_0} = \frac{\alpha_{mi}}{\mu _0} [/math]

The tilde notation above denotes the Fourier transform of the field components in the frequency domain. Transforming the above equations back to the time domain, one encounters convolution on the right hand side due to the frequency dependence of the stretched coordinate metrics:

[math] \left(\varepsilon_x \frac{\partial E_x}{\partial t} + \sigma_{ex}E_x \right) = \breve{s}_{ey}(t) \frac{\partial H_z}{\partial y} - \breve{s}_{ez}(t)\frac{\partial H_y}{\partial z} [/math]

[math] \left(\mu_x \frac{\partial H_x}{\partial t} + \sigma_{mx}H_x \right) = -\breve{s}_{my}(t)\frac{\partial E_z}{\partial y} + \breve{s}_{mz}(t)\frac{\partial E_y}{\partial z} [/math]

where š_ei(t) and š_mi(t) denote functions of time that are indeed the inverse Laplace transform of s_ei^-1 and s_mi^-1,respectively, given by:

[math] \breve{s}_{ei}(t) = \frac{\delta(t)}{\kappa_{ei}} - \frac{\sigma_{ei}}{\kappa_{ei}^2} u(t)\exp \left[-\left(\frac{\sigma_{ei}}{\kappa_{ei}} + \alpha_{ei} \right)\frac{t}{\varepsilon_0} \right] [/math]

[math] \breve{s}_{mi}(t) = \frac{\delta(t)}{\kappa_{mi}} - \frac{\sigma_{mi}}{\kappa_{mi}^2} u(t)\exp \left[-\left(\frac{\sigma_{mi}}{\kappa_{mi}} + \alpha_{mi} \right)\frac{t}{\mu_0} \right] [/math]

where d(t) and u(t) denote the Dirac delta and unit step functions, respectively. The convolutions on the right hand side of the time domain equations can be accelerated by the use of the recursive convolution (RC) method.

The CPML parameters are chosen to be an increasing function of the distance from the boundaries of the computational domain. EM.Cube uses a polynomial profile of degree n_PML. Given the interrelationships among these parameters, one can write:

[math] \sigma_{ei}(r) = \frac{\varepsilon_0}{\mu_0}\sigma_{mi}(r) = \sigma_{max}\left( \dfrac{r}{\delta} \right)^{n_{PML}} [/math]

[math] \kappa_{ei}(r) = \kappa_{mi}(r) = 1 + \left( \kappa_{max} - 1 \right) \left( \dfrac{r}{\delta} \right)^{n_{PML} } [/math]

[math] \alpha_{ei}(r) = \frac{\varepsilon_0}{\mu_0} \alpha_{mi}(r) = \alpha _{min} + \left(\alpha_{max } - \alpha_{min } \right) \left( \frac{r}{\delta} \right)^{n_{PML}} [/math]

where r is the distance of field observation point inside the CPML layer from the edge of the computational domain. The parameters σ_max, κ_max, α_min and α_max as well as n_PML can be modified by the user.

EM.Tempo's Waveform Types

The accuracy of the FDTD simulation results depends on the right choice of temporal waveform. The excitation waveform is the temporal source function that sets the initial conditions at t = 0 and provides an excitation signal afterwards. EM.Tempo currently offers four different choices:

• Sinusoidal
• Gaussian Pulse
• Modulated Gaussian Pulse
• Custom

EM.Tempo's default waveform choice is a modulated Gaussian pulse. If you use a Gaussian pulse or a modulated Gaussian pulse waveform to drive your FDTD source, after a certain number of time steps, the total energy of the computational domain drops to very negligible levels. At that point, you can consider your solution to have converged. If you drive your FDTD source by a sinusoidal waveform, the total energy of the computational domain will oscillate indefinitely, and you have to force the time loop to terminate after a certain number of time steps assuming a steady state have been reached.

EM.Tempo's standard sinusoidal excitation waveform.

EM.Tempo's standard Gaussian pulse excitation waveform.

EM.Tempo's standard modulated Gaussian pulse excitation waveform.

Waveform, Bandwidth, Stability

The FDTD method provides a wideband simulation of your physical structure. Frequency domain techniques often require a tedious frequency sweep to calculate the port characteristics (S/Y/Z parameters). By contrast, EM.Tempo performs a discrete Fourier transform (DFT) of the time domain data to calculate these characteristics at the end of a single FDTD simulation run. In order to produce sufficient spectral information, an appropriate wideband temporal waveform is needed to excite the physical structure. The general form of EM.Tempo's default excitation waveform is a Modulated Gaussian Pulse given by:

[math] E_j^{inc}(r,t)=E_0(r) \exp \left(-\frac{(t-t_0)^2}{\tau ^2} \right) \cos \left(2\pi f_0 (t-t_0)-\Phi \right),\quad j=x,y,z [/math]

where f₀ is the center frequency, t₀ is the time delay, t is the Gaussian pulse width, and Φ is a constant phase. In the limits, the above waveform can be reduced either to a simple Gaussian pulse:

[math] E_j^{inc}(r,t) = E_0(r) \exp \left(-\frac{(t-t_0)^2}{\tau ^2} \right),\quad j=x,y,z [/math]

or to a continuous, single-tone, sinusoidal waveform with a frequency of f₀:

[math] E_j^{inc}(r,t) = E_{0} (r)\cos (2\pi f_0 (t-t_0)-\Phi),\quad j=x,y,z [/math]

The choice of the waveform, its bandwidth and time delay are important for the convergence behavior of the FDTD time marching loop. By default, EM.Tempo uses a modulated Gaussian waveform with optimal parameters: t = 0.966/Δf and t₀ = 4.5t, where Δf is the specified bandwidth of the simulation. The time delay t₀ is chosen so that the temporal waveform has an almost zero value at t = 0. Of the above waveforms, modulated Gaussian and sinusoidal waveforms are band pass with no DC content, while the Gaussian pulse is low pass with a frequency spectrum that is concentrated around f = 0. In a typical FDTD simulation, you set a center frequency for the structure of interest and then specify a bandwidth around this center frequency. These together determine the lowest and highest spectral contents of your FDTD waveform. Note that setting a bandwidth equal to 2f₀ sets the lowest frequency to DC (f_min = 0), which you may want to avoid in certain applications. On the other hand, using a Gaussian pulse waveform, you do want to set Δf = 2f₀. In contrast to the wideband, exponentially decaying, Gaussian pulse and modulated Gaussian waveforms, the sinusoidal waveform is extremely narrowband and single-frequency indeed. It does not decay over time and continues to oscillate indefinitely after reaching a steady state.

Another issue of concern in an FDTD simulation is the numerical stability of the time marching scheme. You can set the mesh grid cell size to any fraction of a wavelength. Normally, you would expect to get better and more accurate results if you increase the mesh resolution. However, the time step is inversely proportional to the maximum grid cell size in order to satisfy the Courant-Friedrichs-Levy (CFL) stability condition:

[math] \Delta t \le \frac{K_{CFL}} {c\sqrt{\left(\dfrac{1}{\Delta x_{min}} \right)^2 + \left(\dfrac{1}{\Delta y_{min}} \right)^2 + \left(\dfrac{1}{\Delta z_{min}} \right)^2 } } [/math]

where c is the speed of light, and K_CFL is a constant. EM.Tempo uses a default value of K_CFL = 0.9. For a uniform grid with equal cell dimensions along the X, Y and Z directions, i.e. Δx = Δy = Δz = Δ, and the CFL condition reduces to:

[math] \Delta t \le K_{CFL} \frac{\Delta}{\sqrt{3}c}[/math]

As can be seen from the above criterion, a high resolution mesh requires a smaller time step. Since you need to let the fields in the computational domain fully evolve over time, a smaller time step will require a larger number of time steps to achieve convergence. EM.Tempo automatically chooses a time step that satisfies the CFL condition.

The Relationship Between Excitation Waveform and Frequency-Domain Characteristics

The accuracy of the FDTD simulation results depends on the right choice of temporal waveform. At the end of an FDTD simulation, the time domain field data are transformed into the frequency domain at your specified frequency or bandwidth to produce the desired observables. The frequency at which the frequency-domain characteristics are computed is usually the same as the center frequency of your project, but it doesn't have to be as long as it falls within the project's bandwidth. Different waveforms have different spectral behaviors. It is critical that you understand the time-domain-to-frequency-domain transformations in order to correctly interpret some simulation data.

If you open up the property dialog of any source type in EM.Tempo, you will see an Excitation Waveform... button located in the "Source Properties" section of the dialog. Clicking this button opens up EM.Tempo's Excitation Waveform dialog. From this dialog, you can override EM.Tempo's default waveform and customize your own temporal waveform.

The sinusoidal waveform has a frequency f₀ equal to the project's center frequency and does not have any parameter that you can modify. The delay in this case is set to t₀ = 1/(4f₀) so that the waveform vanishes at t = 0:

where sinc(x) = sin(πx) / (πx), and T is the length of the temporal window from t = 0 to the exit time t = NΔt, and Δt is the time step of the time marching loop.

For Gaussian and modulated Gaussian waveforms you can set the pulse width and time delay. The pulse width should be chosen such that the Fourier transform of your selected waveform encompasses your project bandwidth. Rather than setting an arbitrary pulse width, EM.Cube lets you set a parameter called Spectral Truncation Level or delta (δ), which is the normalized truncation threshold for the spectral content of the excitation pulse. This is explained as follows. Recall that the Fourier transform of a Gaussian pulse is also a Gaussian pulse. The Fourier transform of a modulated Gaussian pulse consists of two Gaussian pulses located at the two opposite sides of f = 0 (DC) shifted by the modulation frequency f₀:

Since a Gaussian pulse waveform has considerable DC content, it must be used to model lowpass structures. In that case, the center frequency and bandwidth of the project must be set such that Δf = 2f₀ and hence, f_min = f₀ - Δf/2 = 0, and f_max = f₀ + Δf/2 = 2f₀. The width τ of the temporal Gaussian pulse is then determined such that at f_max the spectral Gaussian pulse drops to the δ-level from its maximum value of 1. With a bandwidth of Δf, the pulse width must satisfy the following equation:

[math] \exp[-(\pi f_{\delta} \tau)^2] = \exp[-(\pi \Delta f \tau)^2] = \delta \quad \Rightarrow \quad \tau = \frac{\sqrt{-\ln\delta}}{\pi f_{max}} [/math]

When you set δ = 0.1 (the default value), it means that the Fourier transform of your excitation waveform drops to 10% of its peak at the upper edge of your specified frequency range. For a Modulated Gaussian pulse waveform with a bandwidth of Δf, the pulse width must satisfy the following equation:

[math] \exp[ -[\pi(f_{\delta} - f_0)\tau] ^2 ] = \exp \left[ -\left(\pi \frac{\Delta f}{2} \tau\right)^2 \right] = \delta \quad \Rightarrow \quad \tau = \frac{2\sqrt{-\ln \delta}}{\pi \Delta f} [/math]

For the default value of δ = 0.1, you get the standard relation: τ = 0.966 / BW, which is typically used for modulated Gaussian waveforms. The source waveform requires a time delay t₀ so that its value drops to almost zero at t = 0. The time delay is expressed in terms of a multiple of the pulse width: t0 / tau, and its default value is 4.5.

Keep in mind that FDTD is a time domain algorithm. At the end of an FDTD simulation, a Discrete Fourier Transform (DFT) is performed on the time domain data to calculate frequency domain characteristics such as near fields, far field radiation patterns, RCS, S/Y/Z parameters, etc.:

[math]\tilde{F}(f) = \int_{-\infty}^{\infty} f(t) e^{-j2\pi f t} \, dt \quad \approx \quad \Delta t \sum_{n=0}^N f(n\Delta t) e^{-j2 \pi n f \Delta t} [/math]

Of EM.Tempo's observables, the near fields, far fields and all of their associated parameters like directivity, RCS, etc., are calculated at a certain frequency that is specified as part of the definition of the observable. On the other hand, port characteristics like S/Y/Z parameters, VSWR and periodic characteristics like reflection and transmission coefficients, are calculated over the entire specified bandwidth of your project. In other words, you get a wideband frequency response at the end of a single time domain FDTD simulation run. The number of frequency point data over this bandwidth is equal to the number of DFT samples that are generated during the time marching loop. This number is set to 200 by default. In other words, 200 frequency data are generated at the end of an FDTD simulation. You can change this number through the box labeled No. DFT Samples in the "Discrete Fourier Transform" section of the FDTD Simulation Engine Settings dialog.

Normalization of Frequency-Domain Field Data

From the above equations, it can be seen that the discrete Fourier transform multiplies the samples of time-domain field quantities by the time step Δt. This means that the resulting Fourier transforms of electric and magnetic field components now have units of V/m/Hz or A/m/Hz, respectively. Moreover, the Fourier transforms of the three waveform types have different spectral values at the observation frequency f₀. This makes it difficult to compare the FDTD simulation results with the results from EM.Cube's other computational modules. For example, in the Planar, MoM3D and Physical Optics Modules, a plane wave source typically has a complex-valued functional form of exp(-jk₀k.r), which has a unit magnitude. In EM.Tempo, the time domain plane wave source has a functional dependence of the following form:

[math] \mathbf{E^{inc}}(r,t) = (E_{\theta}^{inc} \hat{\theta} + E_{\phi}^{inc} \hat{\phi}) f \left[ (t-t_0) - \frac{\mathbf{\hat{k} \cdot r} - l_0}{c} \right] [/math]

where f(t) is the temporal waveform, t₀ is the time delay, l₀ is a spatial shift, and c is the speed of light in the free space. The Fourier transform of the above temporal function evaluated at f = f₀ has an amplitude different than 1. For this purpose, EM.Tempo normalizes the temporal waveform by the magnitude of its Fourier transform at the observation frequency f₀. As a result, a temporal plane source with any of the three waveform types will always create spectral incident source with |E^inc(r, f₀)| = 1. The temporal waveform normalization factors for the three waveform types are given below:

[math] \begin{align} &(N.F.)_{Sinusoidal} = \frac{2}{T} = \frac{2}{N \Delta t} \\ &(N.F.)_{Gaussian} = \frac{ e^{(\pi f_0 \tau)^2} }{ \sqrt{\pi} \tau } = \frac{1}{\sqrt{\pi} \tau \delta^{1/4}} \\ &(N.F.)_{Modulated} = \frac{2}{\sqrt{\pi} \tau} \end{align} [/math]

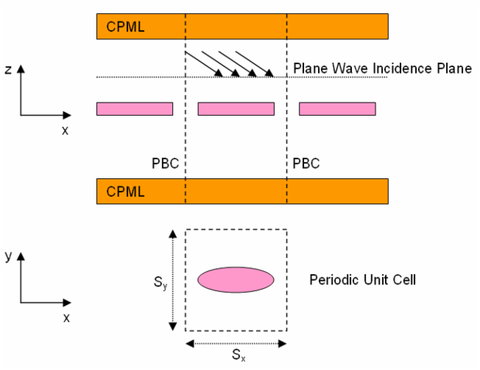
Time Domain Simulation of Periodic Structures

A periodic structure is one that repeats itself infinitely in one, two or three directions. EM.Tempo allows you to simulate doubly periodic structures with periodicities along the X and Y directions. Many interesting structures such as frequency selective surfaces (FSS), electromagnetic band-gap (EBG) structures and metamaterial structures can be modeled using periodic geometries. In the case of an infinitely extended periodic structure, it is sufficient to analyze only a unit cell. In the FDTD method, this is accomplished by applying periodic boundary conditions (PBC) at the side walls of the computational domain. The application of the PBC is straightforward for the case of a normally incident plane wave source since the fields do not experience any delay as they travel across the unit cell. Obliquely incident plane waves, on the other hand, cause a time delay in the transverse plane. This delay requires knowledge of the future values of the fields at any time step.

A number of techniques have been proposed to solve this problem. EM.Cube uses a recently developed novel technique that is known as Direct Spectral FDTD or Constant Transverse Wavenumber method. In this technique, the components of the transverse (horizontal) wavenumber are kept constant in the direction of periodicity. This technique shows a significant advantage over the other methods for simulation of the incident illuminations close to the grazing angles.

Diagram of a periodic structure illuminated by an obliquely incident plane wave in EM.Tempo.

The figure above shows a doubly periodic structure with periods S_x and S_y along the X and Y directions, respectively. The computational domain is terminated with PBC in both X and Y directions. Along the positive and negative Z directions, it is terminated with CPML layers. Bear in mind that the PBC is also applied to the CPML layers. The computational domain is excited by a TM_z or TE_z plane wave incident at z = z₀. The plane wave incidence angles are denoted by θ (elevation) and φ (azimuth) in the spherical coordinate system. The constant wavenumber components k_x and k_y in this case are defined as:

[math]k_x = k_0 \sin\theta\cos\phi[/math]

[math]k_y = k_0 \sin\theta \sin\phi[/math]

where [math]k_0 = \omega/c = 2\pi f/c = 2\pi/\lambda_0[/math] is the free space propagation constant, f is the operational frequency, ω is the angular frequency, λ₀ is the free space wavelength, c is the speed of light in the free space. The constant transverse wavenumber k_l is then given by:

[math] k_l = \sqrt{k_x^2 + k_y^2} = k_0\sin\theta [/math]

which depends only on θ and not on φ. On the excitation plane, the incident field adopts a modulated Gaussian waveform and a complex phase delay along the periodicity direction with the following form:

[math] H_x^{inc}(x,y,t) = -\frac{1}{\eta_0} \sin\phi \; \exp \left(-\frac{(t-t_0)^2}{\tau^2} \right) \exp(j2\pi f_0 t) \exp(-jk_x x) \exp(-jk_y y)[/math]

[math] H_y^{inc}(x,y,t) = \frac{1}{\eta_0} \cos\phi \; \exp \left(-\frac{(t-t_0)^2}{\tau^2} \right) \exp(j2\pi f_0 t) \exp(-jk_x x) \exp(-jk_y y)[/math]

for TM_z polarization and

[math] E_x^{inc}(x,y,t) = \sin\phi \; \exp \left(-\frac{(t-t_0)^2}{\tau^2} \right) \exp(j2\pi f_0 t) \exp(-jk_x x) \exp(-jk_y y)[/math]

[math] E_y^{inc}(x,y,t) = -\cos\phi \; \exp \left(-\frac{(t-t_0)^2}{\tau^2} \right) \exp(j2\pi f_0 t) \exp(-jk_x x) \exp(-jk_y y)[/math]

for TE_z polarization. Here, f₀ is the center frequency of the modulated Gaussian pulse waveform, t₀ is the time delay, and τ is the Gaussian pulse width. The choices of the Gaussian waveform parameters are very critical in order to avoid possible resonances. For a fixed value of k_l, the horizontal resonance occurs at:

[math] f_{res} = \frac{k_l c}{2 \pi} [/math]

For a fixed frequency [math]f_0[/math] and a fixed incidence angle [math]\theta_0[/math], the resonant frequency is reduced to:

[math] f_{res} = f_0 \mathbf{\sin} \theta_0 [/math]

The modulated Gaussian waveform must be chosen such that its effective bandwidth avoids the horizontal resonant frequency. Otherwise, the temporal response of the structure starts to oscillate, and the time marching loop will not converge. To avoid this problem, the modulation frequency and bandwidth of the waveform are chosen to satisfy the following condition:

[math] f_{mod} \ge f_{res} + \dfrac{1}{2}\Delta f = \dfrac{k_{l,fixed}\;c}{2\pi} + \dfrac{1}{2}\Delta f [/math]

Free-Space Wave Propagation

In a free-space line-of-sight (LOS) communication system, the signal propagates directly from the transmitter to the receiver without encountering any obstacles (scatterers). Electromagnetic waves propagate in the form of spherical waves with a functional dependence of e^j(ωt-k₀R)/R, where R is the distance between the transmitter and receiver, [math]\omega = 2\pi f[/math], f is the signal frequency, [math]k_0 = \frac{\omega}{c} = \frac{2\pi}{\lambda}[/math], c is the speed of light, and λ₀ is the free-space wavelength at the operational frequency. By the time the signal arrives at the location of the receiver, it undergoes two changes. It is attenuated and its power drops by a factor of 1/R², and additionally, it experiences a phase shift of [math]\frac{2\pi R}{\lambda_0}[/math], which is equivalent to a time delay of R/c. The signal attenuation from the transmitter to the receiver is usually quantified by Path Loss defined as the ratio of the received signal power (P_R) to the transmitted signal power (P_T). Assuming isotropic transmitting and receiving radiators (i.e. radiating uniformly in all directions), the Path Loss in a free-space line-of-sight communication system is given by Friis’ formula:

[math] \frac{P_R}{P_T} = \left( \frac{\lambda_0}{4\pi R} \right)^2 [/math]

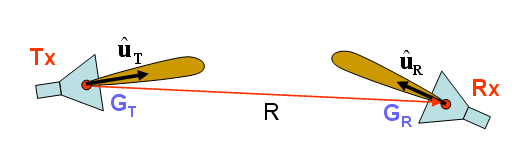
The above formula assumes that the receiving antenna is polarization-matched. Normally, there is a polarization mismatch between the transmitting and receiving antennas. In the case of directional transmitting and receiving antennas, Friis’ formula takes the following form:

[math] P_R = P_T \, G_T G_R \left( \frac{\lambda_0}{4\pi R} \right)^2 \left| \mathbf{ \hat{u}_T \cdot \hat{u}_R } \right|^2 [/math]

where u_T and u_R are the unit polarization vectors of the transmitting and receiving antennas, and G_T and G_R are their gains, respectively.

A line-of-sight (LOS) propagation scenario.

Basic Wave Interaction Mechanisms

EM.Terrano discretizes all of the objects in your propagation scene into flat triangular facets. Obviously, rectangular and cubic objects preserve their geometric shapes through this discretization. Objects with curved surfaces such as cylinders, cones or spheres, are approximated by triangular surface mesh representations. The geometric fidelity of the resulting mesh depends on the specified mesh edge length. When a ray hits a triangular facet, the propagating spherical wave is approximated as a plane wave at the specular point. The reflection and transmission coefficients of the surface are calculated at the operational frequency and at the particular ray incident angle.

A new reflected ray is generated at the specular point, which starts traveling and bouncing around in the scene. If the obstructing surface is penetrable, a second transmitted ray is generated and added to the scene. If the ray hits the edge of an obstacle, it is diffracted from that edge. This leads to the creation of a cone of new rays, which greatly complicate the computational problem. The Uniform Theory of Diffraction (UTD) is used to calculate the wedge diffraction coefficients at the edges of scattering blocks. Note that reflection, transmission and diffraction coefficients are all dependent on the polarization of the incident plane wave.

A receiver may receive a large number of rays: direct line-of-sight rays from the transmitter, rays reflected or diffracted off the ground or terrain, rays reflected or diffracted from buildings or rays transmitted through buildings. Each received ray is characterized by its power, delay and angles of arrival, which are the spherical coordinate angles θ and φ of the incoming ray. The actual signal received and detected by the receiver is the superposition of all these rays with different power levels and different time delays. Most of the time, you will be interested in the coverage map of an area, which shows how much power is received by a grid of receivers spread over the area from a given fixed transmitter.

Ray Reflection & Transmission

The incident, reflected and transmitted rays are each characterized by a triplet of unit vectors:

• [math]( \mathbf{ \hat{u}_{\|}, \hat{u}_{\perp}, \hat{k} } )[/math] representing the incident parallel polarization vector, incident perpendicular polarization vector and incident propagation vector, respectively.
• [math]( \mathbf{ \hat{u}_{\|}^{\prime}, \hat{u}_{\perp}', \hat{k}' } )[/math] representing the reflected parallel polarization vector, reflected perpendicular polarization vector and reflected propagation vector, respectively.
• [math]( \mathbf{ \hat{u}_{\|}^{\prime\prime}, \hat{u}_{\perp}^{\prime\prime}, \hat{k}^{\prime\prime} } )[/math] representing the transmitted parallel polarization vector, transmitted perpendicular polarization vector and transmitted propagation vector, respectively.

The incident, reflected and transmitted rays at the interface between two dielectric media.

The reflected ray is assumed to originate from a virtual image source point. The three triplets constitute three orthonormal basis systems. Below, it is assumed that the two dielectric media have permittivities ε₁ and ε₂, and permeabilities μ₁ and μ₂, respectively. A lossy medium with a conductivity σ can be modeled by a complex permittivity ε_r = ε'_r –jσ/ε₀. Assuming n to be the unit normal to the interface plane between the two media, and Z₀ = 120Ω , the incident polarization vectors as well as all the reflected and transmitted vectors are found as:

[math] \mathbf{ \hat{u}_{\perp} = \frac{\hat{k} \times \hat{n}}{|\hat{k} \times \hat{n}|} } [/math]

[math] \mathbf{ \hat{u}_{\|} = \hat{u}_{\perp} \times \hat{k} } [/math]

The reflected unit vectors are found as:

[math] \mathbf{ \hat{k}' = \hat{k} - 2(\hat{k} \cdot \hat{n}) \hat{n} } [/math]

[math] \mathbf{ \hat{u}_{\perp}' = \hat{u}_{\perp} } [/math]

[math] \mathbf{ \hat{u}_{\|}' = \hat{u}_{\perp}' \times \hat{k}' } [/math]

The transmitted unit vectors are found as:

[math] \mathbf{ \hat{k}^{\prime\prime} = \hat{n} \times a - \sqrt{1-a \cdot a} \; \hat{n} } [/math]

[math] \mathbf{ \hat{u}_{\perp}^{\prime\prime} = \hat{u}_{\perp} } [/math]

[math] \mathbf{ \hat{u}_{\|}^{\prime\prime} = \hat{u}_{\perp}^{\prime\prime} \times \hat{k}^{\prime\prime} } [/math]

where

[math] \mathbf{a} = (k_1/k_2) \mathbf{\hat{k} \times \hat{n}}[/math]

[math] k_1 = k_0 \sqrt{\varepsilon_1 \mu_1} [/math]

[math] k_2 = k_0 \sqrt{\varepsilon_2 \mu_2} [/math]

[math] \eta_1 = Z_0 \sqrt{\mu_1 / \varepsilon_1} [/math]

[math] \eta_2 = Z_0 \sqrt{\mu_2 / \varepsilon_2} [/math]

[math] \sin\theta^{\prime\prime} = \frac{k_1}{k_2}\sin\theta \text{ if } \sin\theta \le k_2/k_1[/math]

The reflection coefficients at the interface are calculated for the two parallel and perpendicular polarizations as:

[math] R_{\|} = \frac { \eta_2(\mathbf{ \hat{k}^{\prime\prime} \cdot \hat{n} }) - \eta_1(\mathbf{ \hat{k} \cdot \hat{n} }) } { \eta_2(\mathbf{ \hat{k}^{\prime\prime} \cdot \hat{n} }) + \eta_1(\mathbf{ \hat{k} \cdot \hat{n} }) } = \frac{\eta_2 \cos\theta^{\prime\prime} - \eta_1 \cos\theta} {\eta_2 \cos\theta^{\prime\prime} + \eta_1 \cos\theta} = \frac{Z_{2\|} - Z_{1\|}} {Z_{2\|} + Z_{1\|}} [/math]

[math] R_{\perp} = \frac { \eta_2(\mathbf{ \hat{k} \cdot \hat{n} }) - \eta_1(\mathbf{ \hat{k}^{\prime\prime} \cdot \hat{n} }) } { \eta_2(\mathbf{ \hat{k} \cdot \hat{n} }) + \eta_1(\mathbf{ \hat{k}^{\prime\prime} \cdot \hat{n} }) } = \frac{\eta_2 / \cos\theta^{\prime\prime} - \eta_1 / \cos\theta} {\eta_2 / \cos\theta^{\prime\prime} + \eta_1 / \cos\theta} = \frac{Z_{2\perp} - Z_{1\perp}} {Z_{2\perp} + Z_{1\perp}} [/math]

Penetration through Thin Walls or Surfaces

In "Thin Wall Approximation", we assume that an incident ray gives rise to two rays, one is reflected at the specular point, and the other is transmitted almost in the same direction as the incident ray. The reflected ray is assumed to originate from a virtual image source point. Similar to the case of reflection and transmission at the interface between two dielectric media, here too we have three triplets of unit vectors, which all form orthonormal basis systems.

The incident and transmitted rays through a thin wall.

The transmission coefficients are calculated for the two parallel and perpendicular polarizations as:

[math] T_{\|} = \frac{(1-{\Gamma_{\|}}^2) \exp(-jk_2 d (\mathbf{ \hat{k}^{\prime\prime} \cdot \hat{n}}))} { 1-{\Gamma_{\|}}^2 \exp( -2jk_2 d (\mathbf{ \hat{k}^{\prime\prime} \cdot \hat{n} }) ) } [/math]

[math] T_{\perp} = \frac{(1-{\Gamma_{\perp}}^2) \exp(-jk_2 d (\mathbf{ \hat{k}^{\prime\prime} \cdot \hat{n}}))} { 1-{\Gamma_{\perp}}^2 \exp( -2jk_2 d (\mathbf{ \hat{k}^{\prime\prime} \cdot \hat{n} }) ) } [/math]

where

[math] \Gamma_{\|} = \frac{ \eta_2(\mathbf{ \hat{k}^{\prime\prime} \cdot \hat{n} }) - \eta_1(\mathbf{ \hat{k} \cdot \hat{n} }) } { \eta_2(\mathbf{ \hat{k}^{\prime\prime} \cdot \hat{n} }) + \eta_1(\mathbf{ \hat{k} \cdot \hat{n} }) } = \frac{\eta_2 \cos\theta^{\prime\prime} - \eta_1 \cos\theta} {\eta_2 \cos\theta^{\prime\prime} + \eta_1 \cos\theta} = \frac{Z_{2\|} - Z_{1\|}} {Z_{2\|} + Z_{1\|}} [/math]

[math] \Gamma_{\perp} = \frac{ \eta_2(\mathbf{ \hat{k} \cdot \hat{n} }) - \eta_1(\mathbf{ \hat{k}^{\prime\prime} \cdot \hat{n} }) } { \eta_2(\mathbf{ \hat{k} \cdot \hat{n} }) + \eta_1(\mathbf{ \hat{k}^{\prime\prime} \cdot \hat{n} }) } = \frac{\eta_2 / \cos\theta^{\prime\prime} - \eta_1 / \cos\theta} {\eta_2 / \cos\theta^{\prime\prime} + \eta_1 / \cos\theta} = \frac{Z_{2\perp} - Z_{1\perp}} {Z_{2\perp} + Z_{1\perp}} [/math]

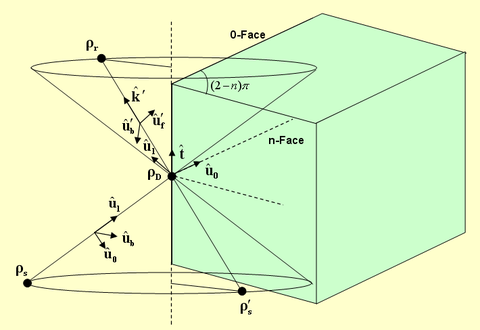
Wedge Diffraction from Edges

For the purpose of calculation of diffraction from building edges, we define a "Wedge" as having two faces, the 0-face and the n-face. The wedge angle is a = (2-n)p, where the parameter n is required for the calculation of diffraction coefficients. All the diffracted rays lie on a cone with its vertex at the diffraction point and a wedge angle equal to the angle of incidence in the opposite direction. A diffracted ray is assumed to originate from a virtual image source point. Three triplets of unit vectors are defined as follows:

• [math]\mathbf{(\hat{u}_0, \hat{u}_l, \hat{t})}[/math] representing the unit vector normal to the edge and lying in the plane of the 0-face, the unit vector normal to the 0-face, and the unit vector along the edge, respectively.
• [math]\mathbf{(\hat{u}_f, \hat{u}_b, \hat{t})}[/math] representing the incident forward polarization vector, incident backward polarization vector and incident propagation vector, respectively.
• [math]\mathbf{(\hat{u}_f', \hat{u}_b', \hat{t}')}[/math] representing the diffracted forward polarization vector, diffracted backward polarization vector and diffracted propagation vector, respectively.

The incident ray and diffracted ray cone at the edge of a building.

The three triplets constitute three orthonormal basis systems. The propagation vector k' of the diffracted ray has to be constructed based on the diffraction cone as follows:

[math] \mathbf{\hat{k}'} = \cos\phi_w \mathbf{\hat{u}_0} + \sin\phi_w \mathbf{\hat{u}_l} + \mathbf{(\hat{k} \cdot \hat{t}) \hat{t}}, \quad 0 \le \phi_w \le \alpha[/math]

where the resolution of the angle θ_w is chosen to be the same as the resolution of the incident ray.

The other unit vectors for the incident and diffracted rays are found as:

[math] \mathbf{ \hat{u}_f = \frac{\hat{k} \times \hat{t}}{|\hat{k} \times \hat{t}|} } [/math]

[math] \mathbf{ \hat{u}_b = \hat{k} \times \hat{u}_f } [/math]

[math] \mathbf{ \hat{u}_f' = \frac{\hat{k}' \times \hat{t}}{|\hat{k}' \times \hat{t}|} } [/math]

[math] \mathbf{ \hat{u}_b' = \hat{k}' \times \hat{u}_f' } [/math]

The diffraction coefficients are calculated in the following way:

[math] D_s = \frac{-e^{-j\pi/4}}{2n \sqrt{2\pi k} \sin\beta_0'} \left\lbrace \begin{align} & \cot \left(\frac{\pi + (\phi-\phi')}{2n}\right) F[kLa^+(\phi-\phi')] + \cot \left(\frac{\pi - (\phi-\phi')}{2n}\right) F[kLa^-(\phi-\phi')] + \\ & R_{0 \perp} \cot \left(\frac{\pi - (\phi+\phi')}{2n}\right) F[kLa^-(\phi+\phi')] + R_{n \perp} \cot \left(\frac{\pi + (\phi+\phi')}{2n}\right) F[kLa^+(\phi+\phi')] \end{align} \right\rbrace [/math]

[math] D_h = \frac{-e^{-j\pi/4}}{2n \sqrt{2\pi k} \sin\beta_0'} \left\lbrace \begin{align} & \cot \left(\frac{\pi + (\phi-\phi')}{2n}\right) F[kLa^+(\phi-\phi')] + \cot \left(\frac{\pi - (\phi-\phi')}{2n}\right) F[kLa^-(\phi-\phi')] + \\ & R_{0 \|} \cot \left(\frac{\pi - (\phi+\phi')}{2n}\right) F[kLa^-(\phi+\phi')] + R_{n \|} \cot \left(\frac{\pi + (\phi+\phi')}{2n}\right) F[kLa^+(\phi+\phi')] \end{align} \right\rbrace [/math]

where F(x) is the Fresnel Transition function:

[math] F(x) = 2j \sqrt{x} e^{jx} \int_{\sqrt{x}}^{\infty} e^{-j\tau^2} \, d\tau [/math]

In the above equations, we have

[math] \begin{align} s = |\rho_D - \rho_S| \\ s' = |\rho_D - \rho_r| \end{align} [/math]

[math]L = \frac{s s' \sin^2 \beta'}{s + s'} [/math]

[math]a^{\pm}(\nu) = 2\cos^2 \left( \frac{2n\pi N^{\pm} - \nu}{2} \right), \quad \nu = \phi \pm \phi' [/math]

where [math]N^{\pm}[/math] are the integers which most closely satisfy the equations [math] 2n\pi N^{\pm} - \nu = \pm \pi [/math].

---

Back to the Top of the Page

Back to EM.Cube Main Page