Hybrid Modeling in EM.Cube Using Multiple Simulation Engines
Contents
- 1 An Integrated Simulation Environment with a Unified User Interface
- 2 Mechanisms for Multi-Engine Simulations
- 3 Using EM.Libera to Generate Hertzian Dipole Sources
- 4 Using EM.Terrano to Genrate Multi-Ray Plane Wave Sources
- 5 Generating Directional Radiators for Import to EM.Terrano
- 6 The Huygens Principle
- 7 Generating Huygens Surface Data
- 8 Defining Huygens Sources
An Integrated Simulation Environment with a Unified User Interface
System-level electromagnetic problems that require multi-scale or multi-technique numerical solutions are very diverse in nature and appear in many engineering disciplines and applications such as communications and radar systems, high-speed digital electronics, microwave photonics, etc. Such problems may involve different length scales ranging from fractions of a wavelength to hundreds or thousands of wavelengths. They may also feature a large variety of geometrical shapes and details as well as complex material variations. In many system-level problems, the overall problem domain is electrically very large, but it may involve many structural details that cannot be ignored in the modeling. Solving the entire problem using a single full-wave technique may not be practical due to enormous memory requirements. On the other hand, oversimplifying the geometry for asymptotic solvers might severely compromise the modeling accuracy. In such cases, you must break up the problem domain into a number of smaller manageable sub-domains (possibly with different length scales) and solve each sub-domain separately using the most suitable and computationally efficient simulation engine.
EM.Cube provides several computational modules featuring simulation engines that are most accurate or efficient for particular classes of problems. These engines represent full-wave, quasi-static and asymptotic techniques in both frequency and time domains. EM.Cube's computational modules have been designed to work with each other seamlessly. For example, all modules share the same user interface and have identical or similar processes to define sources and observables. CubeCAD provides an integrated 3D parametric CAD modeling environment for all the modules. They also share 3D data visualization and the same data manager for generating, manipulating and plotting data on various types of graphs in EM.Grid. Most modules generate similar standard output parameters with identical data file formats. For example, EM.Tempo, EM.Picasso, EM.Libera, EM.Illumina and EM.Terrano all can generate far-field radiation pattern data, which are saved to a radiation data file with a .RAD file extension. EM.Tempo, EM.Picasso, EM.Libera and EM.Illumina can compute radar cross section data and save them to an RCS data file with a .RCS file extension. EM.Tempo, EM.Picasso and EM.Libera can compute the port characteristics of structures that have a port definition. They all generate identical complex-valued S/Z/Y parameter data files with a .CPX file extension. EM.Tempo and EM.Picasso can both generate reflection and transmission coefficient data for periodic surfaces and save them to .CPX data files.
Mechanisms for Multi-Engine Simulations
You can use several of EM.Cube's simulation engines together to solve multi-scale electromagnetic problems. EM.Cube allows interaction among its computational modules through a number of mechanisms. These methods, in essence, consist of using the computed observables of one computational module as the excitation sources of another computational module. For example, you can analyze a wireframe radiating structure using EM.Libera's wire MOM solver and use the computed wire current distribution data as a collection of short dipole sources to excite another structure in a different computational module. Similarly, you can use EM.Terrano to calculate the amplitude and phase of the rays received at a receiver point in a wave propagation scenario, and then import those rays as a collection of plane wave sources to illuminate another structure in a different computational module. You can analyze an antenna structure in EM.Tempo, EM.Picasso, EM.Libera or EM.Illumina and then import the computed polarimetric radiation pattern data to define transmitters or receivers in EM.Terrano. You can use EM.Ferma to compute the capacitance, inductance or resistance of complex sub-wavelength structures and then model them as lumped capacitors, inductors or resistors in EM.Tempo, EM.Picasso or EM.Libera. You can generated the scattering parameters of multiport networks in EM.Tempo, EM.Picasso or EM.Libera and convert the simulation results to a multiport device in RF.Spice A/D complete with a schematic symbol and pin diagram.
Perhaps the most systematic interface among EM.Cube computational modules is the concept of Huygens surface data. According to the electromagnetic equivalence principle, an electromagnetic structure that contains at least one source can be modeled by completely enclosing it inside a closed surface and determining the tangential electric and magnetic fields everywhere on the enclosing surface. Such a closed surface is called a Huygens surface. The known tangential electric and magnetic fields on a Huygens surface act like a new, secondary distributed source that radiates its own electric and magnetic fields either into the same computational domain or into a separate, independent domain. In many problems that involve electrically very large structures or large computational domains, it might be possible to break the entire computational domain into smaller pieces, whose mutual coupling can be neglected. These separate sub-domains can then be solved independently, and the resulting solutions can be assembled together to build the final solution to the original larger problem. Note that in this framework, it is assumed that the elements of the new computational domain do not affect the behavior of the original structure and sources that were enclosed by the Huygens surface.
Using EM.Libera to Generate Hertzian Dipole Sources
Many applications require modeling of wire antennas in the presence of a complex background structure or a platform. An example of this type is a multilayered ground with different cover layers such as soil, snow, ice, vegetation, etc. Such antennas might excite complex surface waves trapped in the substrate layers and may give rise to ducting effects. Another example involves modeling the radiation of a wire antenna or array in the presence of a planar layered structure. Note that EM.Picasso cannot handle wire structures but it can model Hertzian short dipole radiators. In cases like this, one can solve the wire antenna or wire-frame metal structure in EM.Libera using its wire MOM simulation engine assuming that the structure is located far enough above the planar structure so that the latter doesn't affect its current distribution. This process, therefore, involves two steps:
- Solution of the wire structure problem using EM.Libera
- Importing the wire current solution to another module as a set of Hertzian short dipole sources
When you simulate a wire structure in EM.Libera, you can define a Current Distribution observable in your project. Once the wire MOM simulation is completed, the current solution is saved into an ASCII data file with a default name of "MoM.IDI" and a ".IDI" file extension. This file contains the amplitude and phase of each current element (wire cell) as well as its coordinates, length and orientation.
You can import a wire current solution data file with a .IDI file extension as a set of short dipole sources into any EM.Cube module that supports Hertzian short dipole sources. For this purpose, right-click on the Hertzian Short Dipoles item in the "Sources" section of the navigation tree and select Import Dipole Source... from the contextual menu. The standard Windows Open dialog opens up, with the default file type (extension) set to .IDI. Browse your folders to find the right wire current data file and click the Open button of the dialog. This will automatically create a number of short dipole sources in the navigation tree. The number of imported sources is equal to the total number of wire mesh elements in the original EM.Libera project. The amplitude, phase, length and orientation of each source corresponds to one of the wire cell current solutions in the data file. From this point on, the imported dipole radiators behave like regular short dipole sources. You can open the property dialog of each individual source and modify its parameters, if necessary.
Using EM.Terrano to Genrate Multi-Ray Plane Wave Sources
The transmitters and receivers in EM.Terrano are assumed to be point objects or lumped radiators. In the SBR method used by EM.Terrano for ray tracing, the received rays at the location of a receiver are indeed spherical waves that have traveled from the location of the source (transmitter) and have undergone various multipath effects. It is assumed that a receiver always falls into the far-zone field of an actual or virtual transmitter. Therefore, the received rays can be treated as plane waves incident upon the lumped receiver. Invoking the electromagnetic equivalence principle, a point receiver can be treated as a Huygens surface with a number of impinging plane waves upon its faces with different polarizations and different amplitudes and phases. For example, consider a receiving monopole antenna in the presence of a human head model. The monopole and head combination confined in an FDTD domain box in EM.Tempo. This equivalent box can represent a lumped receiver in EM.Terrano. The rays collected at the receiver site can now serve as a set of incident plane wave sources, which excite the FDTD structure. As another example, consider a large receiving patch antenna array at the receiver end in a multipath propagation scenario. In EM.Picasso, the patch array is assumed to have a laterally infinite substrate and ground plane. Therefore, only the rays or plane waves that hit the surface of the patch array from the upper half-space must be considered in its planar MOM simulation. It is evident that this process involves two steps:
- Ray tracing solution of the propagation scene using EM.Terrano
- Importing the ray solution to another module as a set of plane wave sources
An EM.Terrano scene typically has a receiver set that contains a large number of individual receivers arranged as a rectangular grid. You need to select one of these receivers as the import target. At the end of the SBR simulation of your scene, a polarimetric data file with a .PRI extension is created for the selected receiver in the scene. This file contains all the information about the received rays that is needed to define the corresponding plane wave sources in the other EM.Cube modules. However, keep in mind that the ".PRI" file corresponds to a single receiver, which was designated as the "Selected Receiver" at the time of the SBR simulation. By default, the first receiver of a set is designated as the selected receiver.
To import coherent rays as plane wave sources into any EM.Cube module that supports plane wave sources, right-click on the Plane Waves item in the "Sources" section of the navigation tree and select Import SBR Rays... from the contextual menu. The standard Windows Open dialog opens up, with the default file type (extension) set to .PRI. Browse your folders to find the right ray data file and click the Open button of the dialog. This will automatically create a number of plane wave sources in the navigation tree. The number of the imported plane wave sources is either equal to or larger than the total number of received rays by that particular selected receiver.This is due to the fact that each received ray is decomposed to a superposition of two plane wave sources with TMz and TEz polarizations. The incidence angles of the plane wave sources are the same as the rays' angles of arrival.
Generating Directional Radiators for Import to EM.Terrano
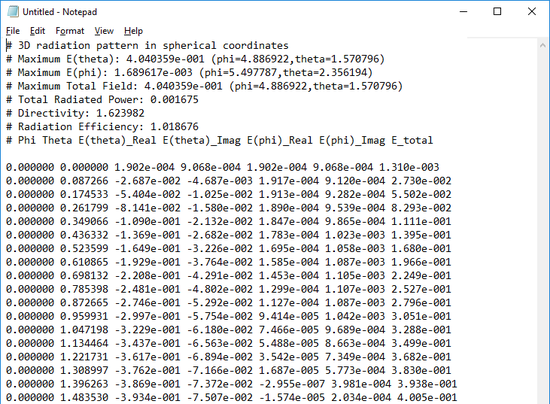
You can use EM.Tempo, EM.Picasso, EM.Libera or EM.Illumina to analyze a large variety of antenna structures either as stand-alone radiators or mounted on complex platforms. All of EM.Cube's computational modules use a common standard file format to store the far-field radiation data. These are ASCII data files with a ".RAD" extension. They contain a list the complex-valued theta and phi components of the far-zone electric field (Eφ and Eθ) as functions of the spherical observation angles φ and θ. The body of the data file consists of seven columns which are separated by a space character. These columns represent:
- Angle Phi in radians
- Angle Theta in radians
- Real part of the Theta component of electrical field in V/m
- Imaginary part of the Theta component of electrical field in V/m
- Real part of the Phi component of electrical field in V/m
- Imaginary part of the Phi component of electrical field in V/m
- Total magnitude of far-zone electric field in V/m
On the other hand, a default transmitter in EM.Teranno is assumed to be a simple vertical half-wave dipole radiator, while the default receiver is assumed to be an isotropic radiator. The complex antenna structures you build and analyze in different EM.Cube modules can be imported to EM.Terrano as a directional "user defined" transmitter and/or receiver. The radiation patterns of these antennas is used to generate weighted rays or beams with the right polarizations by EM.Terrano's SBR simulation engine. This process, therefore, involves two steps:
- Solution of the radiating structure problem using EM.Tempo, EM.Picasso, EM.Libera or EM.Illumina
- Importing the far-field radiation pattern data to EM.Terrano as a directional transmitter an/or receiver
After the simulation of the radiating structure is finished, the far-field radiation pattern data are written into an output data file with a “.RAD” extension that is named after the far-field observable in your project. In EM.Terrano, open the property dialog of a transmitter set or a receiver set. Select the radio button labeled User Defined Antenna for the Radiator Type in these property dialogs. Click the Import Pattern button of the dialog to open the standard Window Open dialog. The file type or extension is automatically set to ".RAD". Browse your folders to find the right radiation pattern data file and click the Open button to set the correct file path. Note that you can also rotate the original imported radiation patterns along the three principal axes.
The spherical far-field components Eφ and Eθ are measured in the far-zone region of the radiating structure, but they are computed and tabulated at a nominal distance of one meter (r = 1m) from the origin of the world coordinate system (WCS). If you multiply these values by (1/r), where r is the distance of the observation point from the origin, you will get the actual values of the electric field components expressed in V/m anywhere in the 3D space. It is obvious that these field values only make sense in the context of the excitation source of the original project that was used to create the radiation pattern data file. When you import a radiation pattern file to a transmitter or receiver in EM.Terrano, by default, it is normalized with respect to the total radiated power. It is this normalized radiation pattern that is used to weight all the transmitted or received rays to model a directional antenna. The property dialog of a transmitter set has an additional check box labeled Custom Power. This box is checked by default, and the transmitter's Baseband Power is set to 1W, which you can modify as you desire. However, if you remove the check mark form the custom power box, then the actual far-field values (not the normalized values) are used to compute the polarization vector of the transmitter rays in all the (θ,φ) directions in the 3D space. This is equivalent to defining a spherical "far-field" Huygens source with a radius of 1m centered at the location of the transmitter. You can use this approach to interface a full-wave solver like FDTD or planar MOM with an asymptotic solver like SBR.
The Huygens Principle
According to the equivalence principle, an electromagnetic structure that contains sources can be modeled by completely enclosing it inside a closed surface and determining the tangential electric and magnetic fields everywhere on the enclosing surface. Such a closed surface is called a Huygens surface. On the Huygens surface, one can write the boundary conditions for the electric and magnetic fields as:
- [math] \mathbf{ \hat{n} \times (H^+ - H^-) = J_s } [/math]
- [math] \mathbf{ \hat{n} \times (E^+ - E^-) = -M_s } [/math]
where n is the outward normal to the Huygens surface at every point of it. The magnetic surface currents have been included in addition to electric surface currents in view of the duality theorem. Assuming zero electric and magnetic fields inside the Huygens surface, one can define equivalent electric and magnetic surface currents on the closed Huygens surface in the following manner:
- [math] \mathbf{ J_s(r) = \hat{n} \times H(r) } [/math]
- [math] \mathbf{ M_s(r) = -\hat{n} \times E(r) } [/math]
The known tangential electric and magnetic fields on a Huygens surface act as new, secondary distributed current sources. These electric and magnetic surface currents are calculated at the end an EM.Cube simulation that has a Huygens Surface Observable observable. The computed Js and Ms data are saved in an ASCII output data file with a ".HUY" file extension. The following EM.Cube modules offer a Huygens surface observable type:
The Huygens electric and magnetic surface currents defined on a specified Huygens surface can be imported to a new project as an excitation source called a Huygens Source. The following EM.Cube modules offer a Huygens source type:
The electric and magnetic surface currents that constitute a Huygens source radiate electric and magnetic fields. They have near-zone and far-zone fields like all other source types. These fields are summed up with the fields due to all the other source types in the project workspace based on the principle of linear superposition.
With a free-space background medium, the electric and magnetic fields radiated by a Huygens source are given everywhere in the space as follows:
- [math] \mathbf{E^{inc}(r)} = -jk_0 \sum_j \iint_{\Delta_j} \, ds' \frac{e^{-jk_0 R}}{4\pi R} \left\lbrace \begin{align} & Z_0 \left[ 1 - \frac{j}{k_0 R} - \frac{1}{(k_0 R)^2} \right] \mathbf{J_j(r')} \\ & -Z_0 \left[ 1 - \frac{3j}{k_0 R} - \frac{3}{(k_0 R)^2} \right] \mathbf{ (\hat{R} \cdot J_j(r')) \hat{R} } \\ & - \left[ 1 - \frac{j}{k_0 R} \right] \mathbf{ (\hat{R} \times M_j(r')) } \end{align} \right\rbrace [/math]
- [math] \mathbf{H^{inc}(r)} = -jk_0 \sum_j \iint_{\Delta_j} \, ds' \frac{e^{-jk_0 R}}{4\pi R} \left\lbrace \begin{align} & Y_0 \left[ 1 - \frac{j}{k_0 R} - \frac{1}{(k_0 R)^2} \right] \mathbf{M_j(r')} \\ & -Y_0 \left[ 1 - \frac{3j}{k_0 R} - \frac{3}{(k_0 R)^2} \right] \mathbf{ (\hat{R} \cdot M_j(r')) \hat{R} } \\ & + \left[ 1 - \frac{j}{k_0 R} \right] \mathbf{ (\hat{R} \times J_j(r')) } \end{align} \right\rbrace [/math]
where the summation over index j is carried out for all the elementary cells Δj that make up the Huygens box. In EM.Cube Huygens surfaces are cubic and are discretized using a rectangular mesh. Therefore, Δj represents any rectangular cell located on one of the six faces of Huygens box. Keep in mind that the fields scattered (or reradiated) by your physical structure do not affect the fields inside the Huygens source.
The far fields of a Huygens source in a free-space background medium are calculated from the following relations:
- [math] \mathbf{E^{ff}(r)} = \frac{jk_0}{4\pi} \frac{e^{-jk_0 r}}{r} \sum_j \iint_{\Delta_j} \left[ Z_0 \, \mathbf{ \hat{r} \times \hat{r} \times J_j(r') } + \mathbf{ \hat{r} \times M_j(r') } \right] e^{ -jk_0 \mathbf{\hat{r} \cdot r'} } \, ds' [/math]
- [math]\mathbf{H^{ff}(r)} = \frac{1}{Z_0} \mathbf{\hat{r} \times E^{ff}(r)} [/math]
In the case of a multilayer planar background medium, the electric and magnetic fields radiated by a Huygens source are given by:
- [math] \mathbf{E^{inc}(r)} = \iint_{S_{HUY}} \mathbf{ \overline{\overline{G}}_{EJ}(r|r') \cdot J_s(r') } \, ds' + \iint_{S_{HUY}} \mathbf{ \overline{\overline{G}}_{EM}(r|r') \cdot M_s(r') } \, ds' [/math]
- [math] \mathbf{H^{inc}(r)} = \iint_{S_{HUY}} \mathbf{ \overline{\overline{G}}_{HJ}(r|r') \cdot J_s(r') } \, ds' + \iint_{S_{HUY}} \mathbf{ \overline{\overline{G}}_{HM}(r|r') \cdot M_s(r') } \, ds' [/math]
Note that the Huygens sources generate near-zone incident fields as given above, which constitute the excitation of your planar structure. In the meantime, they are radiating sources by themselves and also contribute to the far field radiation patterns. These far fields are then superposed with those radiated by the unknown currents that are determined through the MoM solution:
- [math] \mathbf{E^{ff}(r)} = \frac{jk_0}{4\pi} \frac{e^{-jk_0 r}}{r} \left\lbrace \begin{align} & \iint_{S_{HUY}} Z_0 \mathbf{ \hat{r} \times \left[\hat{r} \times \overline{\overline{G}}_{A,ff}(r|r')\right] \cdot J_s(r') } \, ds' + \\ & \iint_{S_{HUY}} \mathbf{ \hat{r} \times \overline{\overline{G}}_{EM,ff}(r|r') \cdot M_s(r') } \, ds' \end{align} \right\rbrace [/math]
Generating Huygens Surface Data
In EM.Tempo, the Huygens box is enclosed inside the FDTD domain box. The six walls of the Huygens box are accommodated into the FDTD mesh's grid. As a results, the number of samples on each face of the Huygens box is determined by the number of the Yee mesh cells on that face. In EM.Terrano, EM.Illumina, EM.Picasso and EM.Libera, a Huygens surface is an arbitrary box centered at coordinates (x0, y0, z0) with dimensions Dx, Dy, and Dz along the three principal directions. It has to enclose the entire finite-sized parts of the physical structure. The number of cells along the three principal directions must additionally be specified in this case.
To define a Huygens surface observable in EM.Tempo, follow these steps:
- Right-click on the Huygens Surfaces item in the "Observables" section of the navigation tree and select Insert New Observable... from the contextual menu.
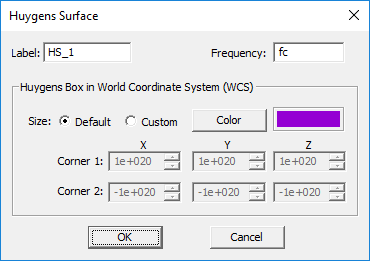
- In the Huygens Surface dialog, use the Label box to change the name of the Huygens surface observable or change the color of the Huygens surface box using the Color button.
- The frequency of surface current calculations can be specified in the box labeled Frequency. By default, this is equal to the center frequency of the project (fc). However, you can calculate the surface current data at any other frequency within the project's bandwidth.
- Define the desired box for surface current calculations in the Huygens Box section of the dialog. As in the case of the far-field radiation pattern observable, there are two options available: a default Huygens box (radio button Size: Default) or a user defined Huygens box (radio buttons Size: Custom). The default Huygens box is identical to the default far-field radiation box, which is placed 0.1λ0 away from the bounding box of the entire physical structure. The custom option allows you to set the Huygens box manually. The values for the coordinates of Corner 1 and Corner 2 can now be changed and set in the world coordinate system (WCS). Corner 1 is the lower-front-left corner and Corner 2 is the upper-rear-right corner of the Huygens box.
To define a Huygens surface observable in EM.Terrano, EM.Illumina, EM.Picasso or EM.Libera, follow these steps:
- Right-click on the Huygens Surfaces item in the "Observables" section of the navigation tree and select Insert New Observable... from the contextual menu.
- In the Huygens Surface dialog, use the Label box to change the name of the Huygens surface observable or change the color of the Huygens surface box using the Color button.
- Enter the values for the coordinates of Corner 1 and Corner 2 of the Huygens box. Corner 1 is the lower-front-left corner and Corner 2 is the upper-rear-right corner of the Huygens box.
- Enter values for the Number of Samples along the X, Y and Z directions. The default values are 10 in all three directions.
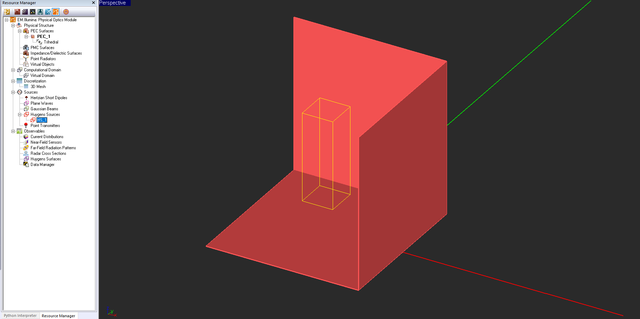
Once you define a Huygens surface observable in the navigation tree, a purple wireframe box according to your specifications appears in the project workspace. You can also define partial Huygens surfaces that would enclose certain objects or sets of objects. Note that if the bottom of your planar structure in EM.Picasso is terminated by a PEC ground plane, then your Huygens box should also terminate on the same ground plane. In that case, the magnetic surface currents vanish on the bottom face of the Huygens box.
Defining Huygens Sources
The Huygens surface data you generate in one of EM.Cube modules can be imported to EM.Illumina, EM.Picasso or EM.Libera as a Huygens source to excite your physical structure. Since the Huygens surface data are computed at a certain frequency, they should be used to excite another physical structure at exactly the same frequency.
To define a Huygens source in EM.Illumina, EM.Picasso or EM.Libera, follow these steps:
- Right-click on the Huygens Sources item in the "Sources" section of the navigation tree and select Insert New Source... from the contaxtual menu.
- The Windows' standard Open dialog opens up, where the file type (extension) is automatically set to .HUY.
- Browse your folders to find the right Huygens data file. Select it and click the Open button of the dialog to import the Huygens source into your project.
- A default red Huygens source box appears in the project workspace, which is identical to the Huygens observable box you saved in the original project.
- Right-click on the new Huygens source's name in the navigation tree and select Properties...from the contextual menu to open its property dialog.
- From the Huygens Source dialog, you can change the label, color, location and orientation of the source. In the section titled Excitation Box, you can view and change the current values of the X, Y and Z coordinates of the source box's center as well as its three Rotation Angles. As you change these coordinates or angles, you will see the box move in the project workspace to a new location or rotate along its local principal axes.
- In the section titled Create Array, you have the option to create an array of identical Huygens source in your project. The Number of Elements along the X, Y and Z directions is 1 by default, denoting a single Huygens source. You can increase the number of elements along each direction and set nonzero values for the Element Spacing along the three principal directions.