EM.Illumina Tutorial Lesson 1: Analyzing The Scattering From Metal Targets
Contents
- 1 What You Will Learn
- 2 Getting Started
- 3 Building a Spherical Target
- 4 Defining the Plane Wave Source
- 5 Defining the Simulation Observables
- 6 Examining the Mesh of the Spherical Target
- 7 Running the Physical Optics Simulation
- 8 3D Visualization of the Simulation Results
- 9 Plotting 2D RCS Graphs
- 10 Verifying Your Simulation Results
What You Will Learn
This tutorial will guide you through all necessary steps required to set up and perform a basic Physical Optics simulation and visualize and graph the simulation results. In particular, you will model scattering of a plane wave from a spherical metal target.
| |
We strongly recommend that you read through the first few tutorials and study them carefully before setting up your own projects. |
![]() Back to EM.Illumina Tutorial Gateway
Back to EM.Illumina Tutorial Gateway
![]() Download projects related to this tutorial lesson
Download projects related to this tutorial lesson
Getting Started
Open the EM.Cube application by double-clicking on its icon on your desktop. By default, EM.Cube opens a blank project with the name “UntitledProj0” in its CubeCAD Module. You can start drawing objects and build up your physical structure right away. Or you can initiate a new project by selecting the New ![]() button of the System Toolbar or using the keyboard shortcut Ctrl+N. This opens up the New Project Dialog, where you can enter a title for your new project and set its path on your hard drive. From the same dialog, you can also set the project’s length units, frequency units, center frequency and bandwidth.
button of the System Toolbar or using the keyboard shortcut Ctrl+N. This opens up the New Project Dialog, where you can enter a title for your new project and set its path on your hard drive. From the same dialog, you can also set the project’s length units, frequency units, center frequency and bandwidth.
For this tutorial lesson, set the following parameters in the new project dialog:
Click the Create button of the dialog to accept the settings. A new project folder with your given name is immediately created at your specified path.
To navigate to EM.Illumina, simply select its icon from the Module Toolbar on the left side of the screen. Selecting the module icon changes the contents of the navigation tree to reflect the types of objects supported by the current module.
Building a Spherical Target
Select the Sphere Tool ![]() button of the Object Toolbar or select the menu item Object → Solid → Sphere.
button of the Object Toolbar or select the menu item Object → Solid → Sphere.
With the sphere tool selected, click at the origin (0,0,0) of the project workspace to start your drawing, and drag the mouse to draw a sphere. Set the Radius of the sphere to R = 600mm. When you drew a very large object, it may full up the entire screen. You can zoom to fit your structure into the screen using the keyboard shortcut Ctrl+E or by clicking the Zoom Extents ![]() button of View Toolbar.
button of View Toolbar.
Note that at the center frequency fo = 1GHz, the operating wavelength is λ0 = 300mm, and your sphere has a diameter of 4λ0.
When you draw an object for the first time in EM.Illumina, a default perfect electric conductor (PEC) group called "PEC_1" is created in the PEC Surfaces node under the Physical Structure section of the navigation tree. In Illumina, objects are grouped together based on their common surface properties. The name of your new object "Sphere_1" appears under the "PEC_1" group. The name of the group is displayed in bold letters, meaning that "PEC_1" is the currently active material group for drawing new objects.
Defining the Plane Wave Source
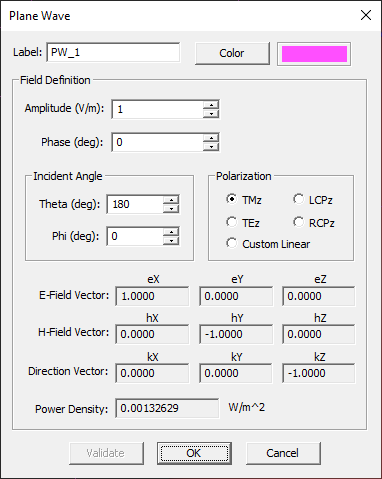
In order to analyze electromagnetic scattering from targets, you illuminate them with a plane wave source and compute the scattered (or reflected) fields. To define a plane wave source, right click on the Plane Waves item of the Sources section in the navigation tree and select Insert New Source… from the contextual menu. The Plane Wave Dialog opens up with a number of default settings. Your plane wave source will have an "Amplitude" of 1V/m and a zero "Phase". You will keep the default TMz polarization. In the “Incident Angle” section of the dialog you need to enter the elevation θ and azimuth φ angles in the standard spherical coordinate system. Accept the default values: θ = 180° and φ = 0°, which represent an X-polarized normally incident plane wave. Note that In EM.Cube, plane waves are characterized by their unit propagation vector. Therefore, for a downward-looking normally incident plane wave, θ = 180°, and for an upward looking wave (along the positive Z-axis), θ = 0°.
After you define the plane wave source, a magenta box appears around your physical structure. A trident also appears at the boundary of the box showing the propagation vector in magenta, the electric polarization vector in dark blue and the magnetic polarization vector in turquoise.
Defining the Simulation Observables
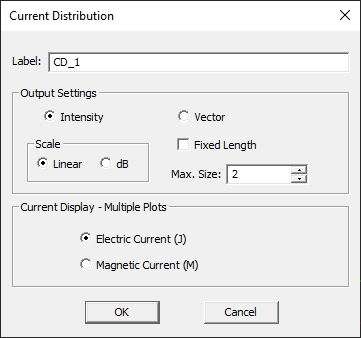
Project observables are output quantities that you would like to compute at the end of a Physical Optics (PO) simulation. By default, EM.Illumina does not generate any output data unless you define one or more project observables before you start a simulation. Current distribution observables are used to visualize the electric and magnetic surface currents on the metallic and dielectric structures. To define a current distribution observable, right-click on the Current Distributions item in the “Observables” section of the navigation tree and select Insert New Observable… This opens up the Current Distribution dialog. Keep all the default options and close the dialog. A new entry CD_1 is added to the navigation tree.
Next, you will define a Radar Cross Section (RCS) observable. Right-click on the Radar Cross Sections item in the navigation tree and select Insert New RCS... from the contextual menu. The Radar Cross Section dialog opens up. In the "RCS Type" section of the dialog, select the default Bistatic RCS option. Change the values of Observation Angle Definition (deg) for both Theta and Phi from the default value of 5° to 1°, and close the dialog. This will set a very high angular resolution for both elevation and azimuth spherical observation angles.
Examining the Mesh of the Spherical Target
EM.Illumina uses a triangular surface mesh generator to discretize the surface and solid CAD objects of your physical structure. The triangular cells are usually generated to be as regular as possible with almost equal surface areas throughout the entire mesh. You can control the mesh resolution by setting the "Mesh Density" expressed as the number of cells per wavelength. The default mesh density is 10 cells per wavelength. This means that on a rectangular plate of dimensions λ0 × λ0, you will have exactly 100 square cells but slightly more than 200 regular triangular cells.
To view the mesh, click the Show/Generate Mesh ![]() button of the Simulate Toolbar or alternatively use the keyboard shortcut Ctrl+M. In general, the mesh view shows how the simulation engine sees your physical structure. To exit the mesh view mode, use the keyboard's "Esc" key or click the Show Mesh button of the Simulate Toolbar one more time.
button of the Simulate Toolbar or alternatively use the keyboard shortcut Ctrl+M. In general, the mesh view shows how the simulation engine sees your physical structure. To exit the mesh view mode, use the keyboard's "Esc" key or click the Show Mesh button of the Simulate Toolbar one more time.
You may notice from the boundary of the mesh that it is not very smooth. The mesh generator first creates a preliminary tessellation of the physical structure and then performs a secondary re-meshing of the tessellated structure. You can improve the overall smoothness by changing the tessellation settings. The mesh properties can be accessed by clicking the Mesh Settings ![]() button of the Simulate Toolbar or using the keyboard shortcut Ctrl+G or by selecting the menu item Simulate → Discretization → Mesh Settings.
button of the Simulate Toolbar or using the keyboard shortcut Ctrl+G or by selecting the menu item Simulate → Discretization → Mesh Settings.
Click the Tessellation Options... button of the mesh settings dialog to changes the tessellation settings.
In the tessellation options dialog, change the default value of Curved Edge Angle Tolerance from 15 to 10 degrees. Click the OK button of this dialog to accept the changes and return to the mesh settings dialog. Now click the Apply button of the mesh settings dialog to regenerate the mesh of your spherical target.
Running the Physical Optics Simulation
At this time, your project is ready for the Physical Optics (PO) simulation of your metal target structure. Click the Run ![]() Button of the Simulate Toolbar to open up the Simulation Run dialog. Or alternatively, use the keyboard shortcut Ctrl+R, or the menu item Simulate → Run… The simplest simulation mode in EM.Illumina is “Single-Frequency Analysis”. In this mode, your physical structure is taken “As Is” and its mesh is passed to the PO simulation engine along with the necessary information regarding the sources and observables.
Button of the Simulate Toolbar to open up the Simulation Run dialog. Or alternatively, use the keyboard shortcut Ctrl+R, or the menu item Simulate → Run… The simplest simulation mode in EM.Illumina is “Single-Frequency Analysis”. In this mode, your physical structure is taken “As Is” and its mesh is passed to the PO simulation engine along with the necessary information regarding the sources and observables.
To run the simulation, click the Run button of the simulation run dialog. A separate window pops up displaying messages from the simulation engine. You can see from the message window that your physical structure involves a total of 10,436 triangular cells.
3D Visualization of the Simulation Results
Once the simulation is completed, the navigation tree is populated with simulation results under the current distributions and RCS nodes. EM.Cube’s computational modules usually generate two types of data: 2D and 3D. Examples of 2D data are Cartesian and polar radiation patterns. Examples of 3D data are near-field and current distributions and 3D radiation patterns. 3D data are visualized in EM.Cube’s project workspace, and the plots are usually overlaid on the physical structure. For this reason, it might be necessary to hide the geometric objects which might obstruct the plots. You can also freeze the geometric objects. In that case, you will see a wireframe outline of the frozen object and you cannot select it. To freeze an object, right-click on its surface in the project workspace or right-click on its name in the navigation tree and select Freeze from the contextual menu.
| |
It is recommended that you freeze objects with curved surfaces in the project workspace before 3D data visualization. |
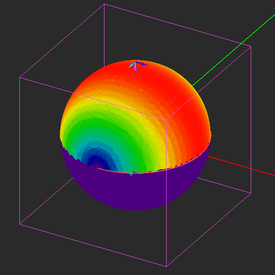
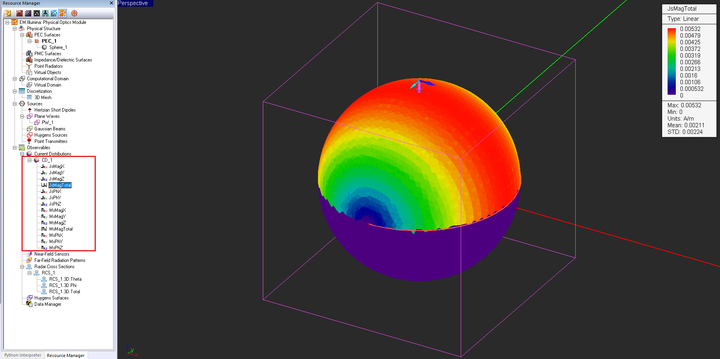
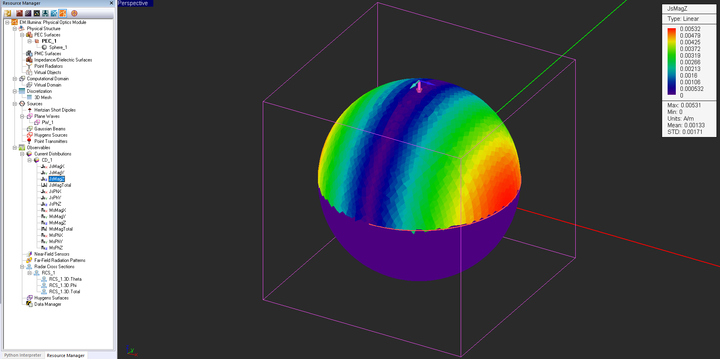
First, you will visualize the current distribution on the metal sphere. The "Current Distribution" section of the navigation tree plots both electric currents (J) and magnetic currents (M). Each current distribution observable contains a list of twelve amplitude and phase plots for all the six current components: Jx, Jy, Jz, and Mx, My, Mz. There are also two additional plots for the magnitude of total electric current and total magnetic current. In the case of your project, since you have only a PEC surface, M = 0. Click on any of these plots to display them in the project workspace. You can use the standard view operations such as dynamic zoom, rotate view, pan view, etc. to better examine these plots.
Next, visualize the 3D RCS of the spherical target by clicking the "RCS_1_3D_Tot" item under Radar Cross Sections in the navigation tree.
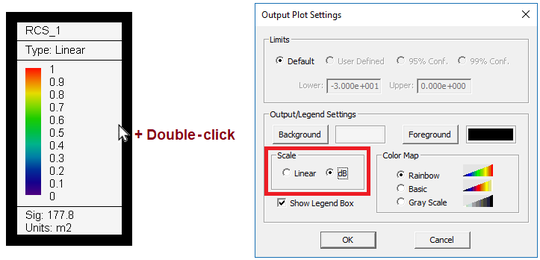
Sometimes it is preferred to plot the RCS on a dB scale. To do so, double-click on the legend box of the plot to open up the Output Plot Settings dialog. You can also open this dialog from the contextual menu of the total 3D RCS item in the navigation tree. In the Scale section of the dialog, select the "dB" radio button. The RCS is now displayed on the dB scale: D0 = 22.5dBm2.
Plotting 2D RCS Graphs
A list of all the 2D output data files generated at the end of a simulation can be viewed in EM.Tempo’s Data Manager. To open this dialog, click the Data Manager ![]() button of Simulate Toolbar, or use the keyboard shortcut Ctrl+D, or select the menu item Simulate → Data Manager.
button of Simulate Toolbar, or use the keyboard shortcut Ctrl+D, or select the menu item Simulate → Data Manager.
Select the data files "RCS_1_RCS_Polar_YZ.CPX" and "RCS_1_RCS_Polar_ZX.CPX" from the list by clicking on their names and highlighting their rows in the table. Click the Plot button of the dialog. A PyPlot graph window pops up that shows the polar graph representing the RCS of your metallic target in the principal YZ and ZX planes.
RCS data are plotted on a linear scale by default. You can also plot them on a dB scale. You are now going to plot the dB-scale Cartesian graphs of RCS in the principal YZ and ZX planes. In the data manager's list, select the data files "RCS_1_RCS_Cart_YZ.CPX" and "RCS_1_RCS_Cart_ZX.CPX" one at a time. Click the Graph Settings button of the data manager to open the "Graph Settings" dialog. From the drop-down list labeled Data Format choose the dB_Power_Scale option.
| |
For RCS plots select the "dB_Power_Scale" option, and for radiation pattern plots select the "dB_Field_Scale" option. |
Close the graph properties dialog and return to the data manager. Do this for both graphs and then plot them.
The 2D RCS graphs show both the theta and phi components as well as the total radar cross section. In the case of your spherical target, the "cross-pol" RCS is much smaller than the "co-pol" RCS. You can customize the graphs and change the scale of the graph axes. Click the Graph Settings button and uncheck the Auto box. For X-Axis, enter values -200 and 200 for Min and Max, respectively, and set the No. Major Intervals to 4 in "Axis Settings" panel. Similarly, for Y-Axis enter values -5, 25, and 6 for Min and Max, and No. Major Intervals respectively. The dynamic range of your graph is now 30dB.
The Cartesian RCS graphs should now look like the figures below. The graphs are interactive. If you move the mouse around the graph, the horizontal and vertical axis values of each data point are displayed on Plot's Status Bar. You can also pan axes with left mouse or zoom with the right mouse by clicking ![]() button of Plot's bottom toolbar.
button of Plot's bottom toolbar.
Verifying Your Simulation Results
To verify the above results, note that the incident magnetic field in the case of TMz polarization is given by:
[math] \mathbf{H^{inc}} = -H_0 \mathbf{\hat{y}} = -\frac{E_0}{\eta_0} \mathbf{\hat{y}} = -\frac{1V/m}{(120\pi)\Omega} \mathbf{\hat{y}} = -0.00265 \mathbf{\hat{y}} A/m [/math]
The zeroth-order physical optics solution for the PEC surface is given by:
[math] \mathbf{J_s} = 2 \mathbf{\hat{n}} \times \mathbf{H^{inc}} [/math]
Consider the following three points on the surface of the sphere:
[math] \mathbf{J_s}(\theta=90^o,\phi=180^o) = 2 (-\mathbf{\hat{x}}) \times (-H_0 \mathbf{\hat{y}}) = 2H_0 \mathbf{\hat{z}} [/math]
[math] \mathbf{J_s}(\theta=0^o,\phi=180^o) = 2 (\mathbf{\hat{z}}) \times (-H_0 \mathbf{\hat{y}}) = 2H_0 \mathbf{\hat{x}} [/math]
[math] \mathbf{J_s}(\theta=45^o,\phi=180^o) = 2 \left( -\frac{\mathbf{\hat{x}}}{\sqrt{2}} + \frac{\mathbf{\hat{z}}}{\sqrt{2}} \right) \times (-H_0 \mathbf{\hat{y}}) = \frac{2H_0}{\sqrt{2}} \left( \mathbf{\hat{x}} + \mathbf{\hat{z}} \right) [/math]
At all the three points, we have:
[math] \left| \mathbf{J_s} \right| = 2H_0 = 2(0.00265) = 0.0053 A/m [/math]
which agrees well with EM.Illumina's computed results.
From classic electromagnetic scattering theory, we know that the back-scattered RCS of a large metallic sphere approaches πr2, where r is the radius of the sphere. The above figure shows the variation of the normalized back-scattered RCS vs. normalized sphere radius k0r = 2πr/λ0, where the three Rayleigh, Mie and optical regions have been indicated. Your spherical target has a radius of 750mm. At an operating frequency of 1GHz, k0r = 12.566. This means that your metallic sphere target falls well into the optical region. Therefore, we can write:
[math] \sigma|_{r \rightarrow \infty } = \pi r^2 = \pi (0.6m)^2 = 1.13m^2 = 0.53dBm^2 [/math]
When your structure is excited by a plane wave source and you have a far-field RCS observable in your project, EM.Illumina computes the forward-scattered RCS (FRCS), back-scattered RCS (BRCS) and maximum RCS (MRCS) at all directions and writes the data into ASCII files accessible through the data manager. Open the data manager dialog and view the contents of the data files "FRCS.DAT" and "BRCS.DAT" by selecting these files and clicking the View button of the dialog. The table below shows the forward-scattered and back-scattered RCS values read from these data files. Note how close the computed value of the back-scattered RCS is to the theoretically predicted value.
| Target | FRCS (linear) | FRCS (dB) | BRCS (linear) | BRCS (dB) |
|---|---|---|---|---|
| PEC Sphere | 177.82 m2 | 22.5 dBm2 | 1.123 m2 | 0.504 dBm2 |