RF Tutorial Lesson 12: Time Domain Simulation of Generic RF Devices
Contents
- 1 What You Will Learn
- 2 Exploring the Wilkinson Power Divider
- 3 Investigating the Dispersion Effects
- 4 Operating the Wilkinson Divider with Unequal Power Split
- 5 Exploring the Branchline Hybrid Coupler
- 6 Feeding a Pulse Waveform to a Branchline Hybrid Coupler
- 7 Exploring the Rat-Race Hybrid Coupler
- 8 Operating the Rat-Race Coupler in Σ-Δ Mode
What You Will Learn
In this tutorial you will explore the operation of several generic RF devices in RF.Spice A/D including Wilkinson Power Divider, Branchline Coupler and Rat-Race Coupler.
Exploring the Wilkinson Power Divider
The following is a list of parts needed for this part of the tutorial lesson:
| Part Name | Part Type | Part Value |
|---|---|---|
| V1 | Voltage Source | Waveform TBD |
| X1 | Wilkinson Power Divider | Defaults, fc = 2G, K = 1 |
| R1 - R3 | Resistor | 50 |
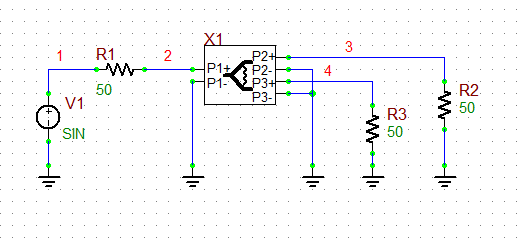
RF.Spice A/D provides two types of power divider: Resistive and Wilkinson. These are reciprocal three-port devices that connect a transmission line port P1 to two other parallel transmission line ports P2 and P3. If you use P1 as the input and P2 and P3 as two outputs, you will have a power splitter. On the other hand, if you use P2 and P3 as two inputs and P1 as the output, you will have a power combiner. Connect the Wilkinson power divider X1 and the three 50Ω resistors as shown in the figure below. Make sure to ground the negative pins of all three ports.
Open the property dialog of the Wilkinson Power Divider and set its frequency to 2GHz. Keep the default values Z0 = 50Ω, eeff = 1 and len = 10mm. It is assumed that the power divider has 10mm T-Line segments at its input and output ports. The K-parameter of the power divider represents the ratio of the power delivered to Port 3 to the power delivered to Port 2. For a 3-dB power splitter, set K = 1:
Define a sinusoidal waveform for your voltage source according to the table below:
| Offset Voltage | 0 |
|---|---|
| Peak Amplitude | 1 |
| Frequency | 2G |
| Delay Time | 0 |
| Damping Factor | 0 |
Run a Transient Test of this circuit with the parameters specified below:
| Start Time | 0 |
|---|---|
| Stop Time | 5n |
| Linearize Step | 1p |
| Step Ceiling | 1p |
| Preset Graph Plots | v(2), v(3), v(4) |
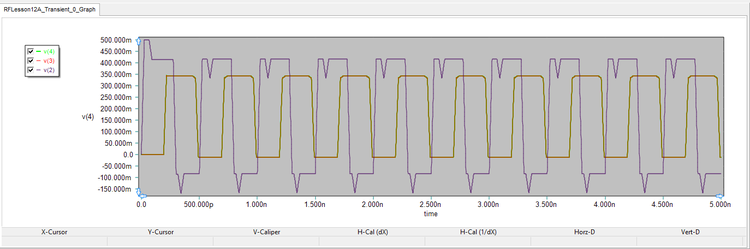
The voltage graphs are shown in the figure below. The input voltage v(2) is seen to be 500mV, which means the voltage source's power is equally split between the source resistor and the Port 1. In other words, we have a perfect input match: z11 = 50Ω and s11 = 0. The output port voltages v(3) and v(4) are both equal to 354mV, which is about 1/√2 times the input voltage v(2).
The ratio the output port powers, therefore, is calculated as:
[math] \frac{P_2}{P_1} = \frac{P_3}{P_1} = \frac{(1/2) R_2 I_2^2}{(1/2) z_{11} I_1^2} = \frac{V_2^2 / (2R_2) }{V_1^2 / (2z_{11}) } = \left( \frac{V_2}{V_1} \right)^2 = \left( \frac{0.354}{0.5} \right)^2 = 0.501 [/math]
[math] \frac{P_3}{P_2} = \frac{(1/2) R_3 I_3^2}{(1/2) R_2 I_2^2} = \frac{V_3^2 / (2R_3) }{V_2^2 / (2R_2) } = \left( \frac{V_3}{V_2} \right)^2 = \left( \frac{0.354}{0.354} \right)^2 = 1 [/math]
Investigating the Dispersion Effects
The Wilkinson power divider does its job well with single-tone harmonic signals. In this part, you will input a pulse train waveforms to see how the transmission line structure of the divider affects the signal integrity. Open the property dialog of the voltage source V1 and define a pulse waveform according to the table below:
| Initial Voltage | 0 |
|---|---|
| Peak Voltage | 1 |
| Delay Time | 0 |
| Rise Time | 25p |
| Fall Time | 25p |
| Pulse Width | 250p |
| Pulse Period | 500p |
Run a Transient Test of your circuit with the parameters specified below:
| Start Time | 0 |
|---|---|
| Stop Time | 5n |
| Linearize Step | 1p |
| Step Ceiling | 1p |
| Preset Graph Plots | v(2), v(3), v(4) |
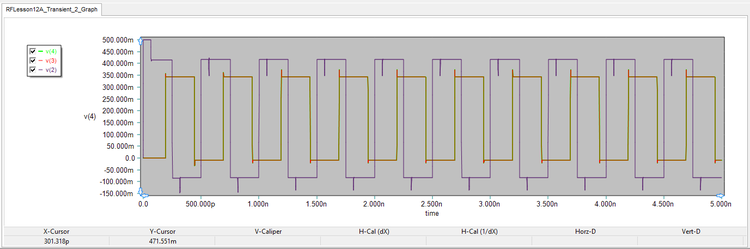
The voltage graphs are shown in the figure below. Note how the input voltage v(2) is distorted and its peak amplitude has dropped to about 400mV. This is due to the fact that Port 1 of the Wilkinson divider is impedance-matched at 2GHz only.
To see the effect of the pulse's rise and fall times, change the waveform one more time as specified below and run a transient test with the same parameters as above.
| Initial Voltage | 0 |
|---|---|
| Peak Voltage | 1 |
| Delay Time | 0 |
| Rise Time | 1p |
| Fall Time | 1p |
| Pulse Width | 250p |
| Pulse Period | 500p |
The voltage graphs are shown in the figure below. Lowering the rise and fall times from 25ps to 1ps helps reduce the distortion of the input voltage but it introduces a slight overshoot at the output waveforms.
Operating the Wilkinson Divider with Unequal Power Split
The Wilkinson power divider can be configured to deliver unequal output powers. Open the property dialog of the Wilkinson Power Divider once again and set K = 2. In the case of unequal power split, the terminating load of the devisers must be unequal, too, according to the following relations:
[math] Z_{L1} = \sqrt{K} Z_0 = \sqrt{2} (50) = 70.71\Omega [/math]
[math] Z_{L2} = Z_0 / \sqrt{K} = 50 / \sqrt{2} = 35.36\Omega [/math]
Restore the sinusoidal waveform of the voltages source V1:
| Offset Voltage | 0 |
|---|---|
| Peak Amplitude | 1 |
| Frequency | 2G |
| Delay Time | 0 |
| Damping Factor | 0 |
The modified circuit is shown in the figure below:
Run a Transient Test of your circuit. However, this time plot the output powers. These are indeed the power of the resistors R1, R2 and R3. They are listed in the Edit Plot List dialog as p(r1), p(r2) and p(r3):
| Start Time | 0 |
|---|---|
| Stop Time | 5n |
| Linearize Step | 1p |
| Step Ceiling | 1p |
| Preset Graph Plots | p(r1), p(r2), p(r3) |
The following figure shows the graph of instantaneous output powers vs. time. The maximum power levels are given in the table below:
| P1 | P2 | P3 | P2+P3 | P3/P2 |
|---|---|---|---|---|
| 5mW | 1.66mW | 3.34mW | 5mW | 2.01 |
Note that the ratio of the maximum output power levels is almost 2:1, and the input port power equals the sum of the two output port powers.
Exploring the Branchline Hybrid Coupler
The following is a list of parts needed for this part of the tutorial lesson:
| Part Name | Part Type | Part Value |
|---|---|---|
| V1 | Voltage Source | Waveform TBD |
| X1 | Branchline Coupler | Defaults, fc = 2G, len = 10 |
| R1 - R4 | Resistor | 50 |
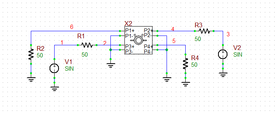
Directional couplers are reciprocal four-port networks. RF.Spice A/D provides two types of hybrid directional coupler: Branchline Coupler and Rat Race Coupler. A Branchline Coupler is a quadrature hybrid. THe opposite figure shows a diagram of a branchline hybrid coupler. Port 1 is used as the input. The power is delivered to the output ports 2 and 3. Port 4 is the isolated port and is terminated in a 50Ω resistor. The output ports 2 and 3 have a 90o phase difference and are both terminated in equal 50Ω resistive loads. Place and connect the parts according to following simple circuit:
Open the property dialog of the Branchline Hybrid and set its frequency to 2GHz. Keep the default values Z0 = 50Ω, eeff = 1 and len = 10mm. It is assumed that the coupler has 10mm T-Line segments at all of its four ports.
Define a sinusoidal waveform for your voltage source according o the table below:
| Offset Voltage | 0 |
|---|---|
| Peak Amplitude | 1 |
| Frequency | 2G |
| Delay Time | 0 |
| Damping Factor | 0 |
Run a Transient Test of this circuit with the parameters specified below:
| Start Time | 0 |
|---|---|
| Stop Time | 5n |
| Linearize Step | 1p |
| Step Ceiling | 1p |
| Preset Graph Plots | v(2), v(3), v(4), v(5) |
The four port voltage graphs are shown in the figure below. The input voltage v(2) is once again 500mV, which means a perfect input match. The output voltages v(3) and v(4) are both equal to 354mV, which is about 1/√2 times the input voltage. In addition, there is a 125ps delay between v(3) and v(4), which is equivalent to a 90o phase difference (T = 500ps). Note that the voltage v(5) at the isolated Port 4 vanishes very quickly.
Your observations are consistent with the scattering matrix of the branchline hybrid coupler:
[math] [S] = \frac{-1}{\sqrt{2}} \left[ \begin{array}{ccc} 0 & j & 1 & 0 \\ j & 0 & 0 & 1 \\ 1 & 0 & 0 & j \\ 0 & 1 & j & 0 \end{array} \right] [/math]
Feeding a Pulse Waveform to a Branchline Hybrid Coupler
In order to understand how the transmission line structure of the branchline hybrid coupler might affect the signal integrity, open the property dialog of the voltage source V1 and define a pulse waveform according to the table below:
| Initial Voltage | 0 |
|---|---|
| Peak Voltage | 1 |
| Delay Time | 0 |
| Rise Time | 25p |
| Fall Time | 25p |
| Pulse Width | 250p |
| Pulse Period | 500p |
Run a Transient Test of your circuit with the parameters specified below:
| Start Time | 0 |
|---|---|
| Stop Time | 5n |
| Linearize Step | 1p |
| Step Ceiling | 1p |
| Preset Graph Plots | v(2), v(3), v(4), v(5) |
The four port voltage graphs are shown in the figure below. The input voltage v(2) is distorted in a similar fashion as you saw earlier in the case of the Wilkinson power divider. What is more alarming is the fact that the voltage v(5) at the isolated Port 4 no longer vanishes. Instead, it steadily maintains a lower bound of about 120mV, which is significant compared to the two output port voltage levels.
Exploring the Rat-Race Hybrid Coupler
The following is a list of parts needed for this part of the tutorial lesson:
| Part Name | Part Type | Part Value |
|---|---|---|
| V1 | Voltage Source | Waveform TBD |
| X2 | Rat-Race Coupler | Defaults, fc = 2G, len = 10 |
| R1 - R4 | Resistor | 50 |
In this part of the tutorial lesson, you will examine RF.Spice's Rat-Race Hybrid . This is primarily used as a 180° coupler as shown in the opposite figure. In this case, Port 3 is used as the input. The power is delivered to the output ports 1 and 4. Port 2 is the isolated port and is terminated in a 50Ω resistor. The output ports 1 and 4 have a 180o phase difference and are both terminated in equal 50Ω resistive loads. Place and connect the parts according to following simple circuit:
Open the property dialog of the Branchline Hybrid and set its frequency to 2GHz. Keep the default values Z0 = 50Ω, eeff = 1 and len = 10mm. It is assumed that the coupler has 10mm T-Line segments at all of its four ports.
Define a sinusoidal waveform for your voltage source according o the table below:
| Offset Voltage | 0 |
|---|---|
| Peak Amplitude | 1 |
| Frequency | 2G |
| Delay Time | 0 |
| Damping Factor | 0 |
Run a Transient Test of this circuit with the parameters specified below:
| Start Time | 0 |
|---|---|
| Stop Time | 5n |
| Linearize Step | 1p |
| Step Ceiling | 1p |
| Preset Graph Plots | v(2), v(3), v(4), v(5) |
The four port voltage graphs are shown in the figure below. The input voltage v(2) is once again 500mV, which means a perfect input match. The output voltages v(5) and v(4) are both equal to 354mV, which is about 1/√2 times the input voltage. In addition, there is a 250ps delay between v(5) and v(4), which is equivalent to a 180o phase difference (T = 500ps). Moreover, the voltage v(3) at the isolated Port 2 vanishes very quickly.
Here, too, you can see that your results are consistent with the scattering matrix of the rat-race hybrid coupler:
[math] [S] = \frac{-j}{\sqrt{2}} \left[ \begin{array}{ccc} 0 & 1 & 1 & 0 \\ 1 & 0 & 0 & 1 \\ 1 & 0 & 0 & -1 \\ 0 & 1 & -1 & 0 \end{array} \right] [/math]
Before closing this section of the tutorial, let's swap the voltage source between Port 3 and Port 1 as shown in the figure below:
In this case, Port 1 acts as the input port, Ports 3 and 2 are the output ports and Port 4 is isolated. Run a transient test with the same sinusoidal waveform and test parameters as before. The figure below shows the four port voltage graphs. Note that in this case the two output ports are in-phase. This is expected from the scattering matrix given above.
Operating the Rat-Race Coupler in Σ-Δ Mode
The following is a list of parts needed for this part of the tutorial lesson:
| Part Name | Part Type | Part Value |
|---|---|---|
| V1 | Voltage Source | Waveform TBD |
| V2 | Voltage Source | Waveform TBD |
| X1 | Rat-Race Coupler | Defaults, fc = 2G, len = 10 |
| R1 - R4 | Resistor | 50 |
One of the interesting functions of the rat-race hybrid coupler is when you feed two of its non-adjacent ports with two different signals. Then, the other two port produce the sum and difference of the two input signals. Place and connect the parts as shown in the figure below:
Initially, use the same sinusoidal waveform for both of your voltage sources:
| Offset Voltage | 0 |
|---|---|
| Peak Amplitude | 1 |
| Frequency | 2G |
| Delay Time | 0 |
| Damping Factor | 0 |
Run a Transient Test of this circuit with the parameters specified below:
| Start Time | 0 |
|---|---|
| Stop Time | 5n |
| Linearize Step | 1p |
| Step Ceiling | 1p |
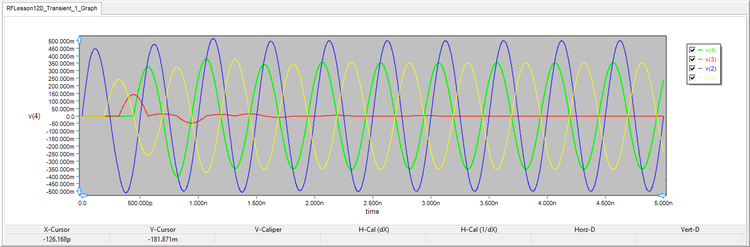
| Preset Graph Plots | v(2), v(4), v(5), v(6) |
The four port voltage graphs are shown in the figure below. The input voltages v(2) and v(4) are 500mV due to the perfect input match. The output voltage v(6) is 707mV, while the other output voltage v(5) vanishes quickly. This is confirms that |v(6)| = |v(2) + v(4)|/√2 and |v(5)| = |v(2) - v(4)|/√2.
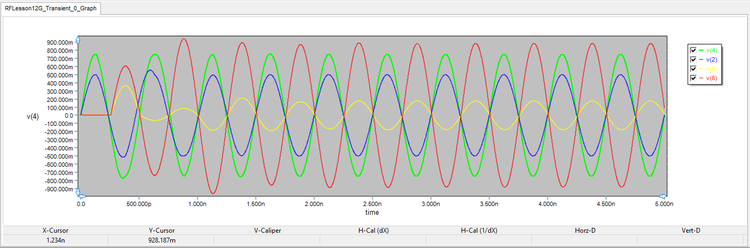
As another try, change the peak amplitude of the second voltage source V2 to 1.5V. Run a new Transient Test of the circuit with the same parameters and view the port voltage graphs as shown below. The following table shows the peak amplitudes of the four port voltage waveforms. The simulated results agree very well with the expected analytical results.
| v(2) | v(4) | V(6) | v(5) | |v(2) + v(4)| /√2 | |v(2) - v(4)| /√2 |
|---|---|---|---|---|---|
| 500mV | 750mV | 884mV | 177mV | 884.02mV | 176.80mV |