EM.Ferma Tutorial Lesson 3: Modeling Objects Immersed In A Uniform Electric Field

What You Will Learn

Previously, you observed that the electric field in the region between the two parallel plates of a capacitor is fairly uniform. In this tutorial you will use parallel metal plates held at different potentials to generate a uniform electric field. Then you will simulate the interaction of this uniform field with immersed objects of different material compositions.

Back to EM.Ferma Manual

Back to EM.Ferma Tutorial Gateway

Download projects related to this tutorial lesson

Getting Started

Open the EM.Cube application and switch to EM.Ferma. Start a new project with the following parameters:

Creating a Uniform Electric Field

Create three Fixed-potential PEC groups in the navigation tree as follows:

Material Group	Material Type	Color	Fixed Potential
PEC_1	PEC	Rosy red (default)	-10V
PEC_2	PEC	Orange	10V
PEC_3	PEC	Pink	0V

Draw the following two rectangle strip objects:

Part	Object Type	Material Type	Dimensions	Coordinates	Rotation Angles
Rect_Strip_1	Rectangle Strip	PEC_1	50mm × 50mm	(0, 0, -10mm)	(0°, 0°, 0°)
Rect_Strip_2	Rectangle Strip	PEC_2	50mm × 50mm	(0, 0, 10mm)	(0°, 0°, 0°)

Open the domain settings dialog and reduce the domain offset to 15mm in all the six directions. Then open the mesh settings dialog and change the fixed mesh cell size to Δ_x = Δ_y = Δ_z = 0.5mm. Define three field sensor observables according to the table below:

Field Sensor	Direction	Coordinates	Plot Type	Max. Size	Cone Length Ratio	Cone Radius Ratio
Sensor_1	Z	(0, 0, 0)	Intensity	-	-	-
Sensor_2	X	(0, 0, 0)	Vector	2	0.75	0.25
Sensor_3	Y	(0, 0, 0)	Intensity	-	-	-

The geometry of the two parallel metal plates with different potentials.

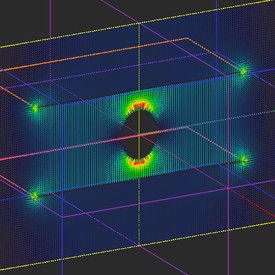
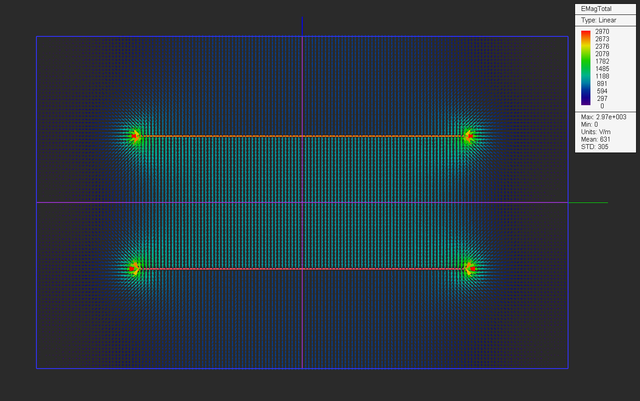
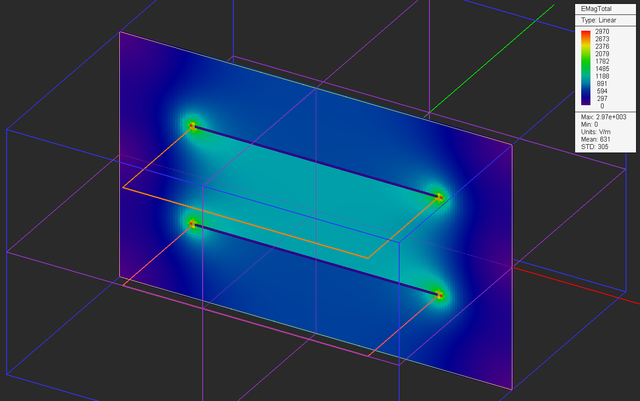
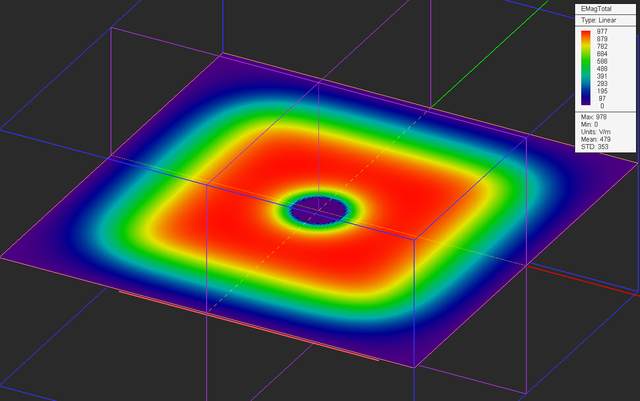
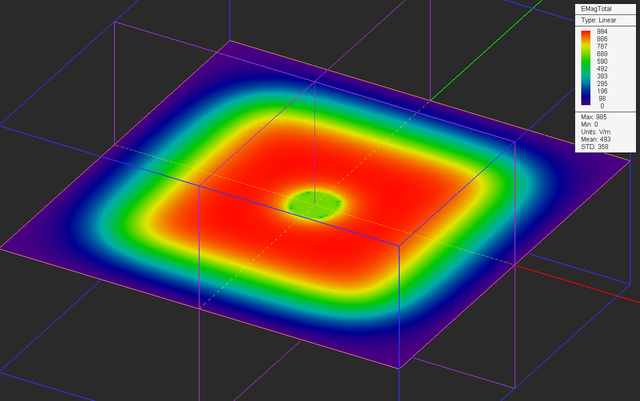
Run an electrostatic analysis of your parallel plate structure and visualize the field distributions on the three sensor planes. You can see a uniform electric field of strength |E| = (20V)/(20mm) = 1000V/m at the center plane.

The electric field distribution in the Sensor_1 (XY) plane.

The electric field distribution in the Sensor_2 (YZ) plane.

The electric field distribution in the Sensor_3 (ZX) plane.

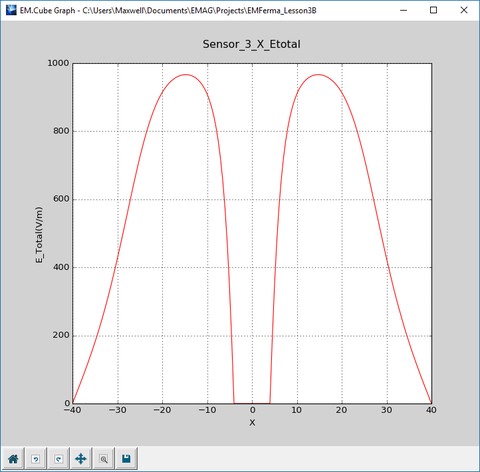
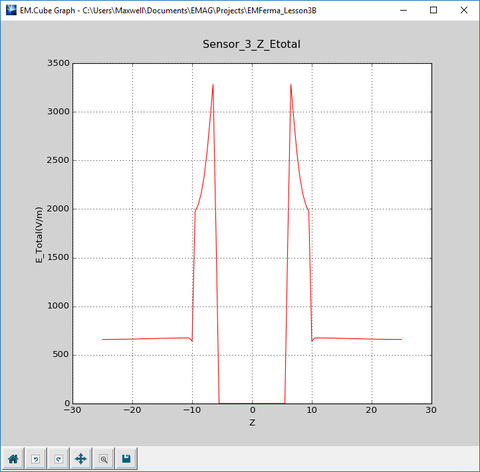
The figures below are the plots of the data files "Sensor_3_X_ETotal.DAT" and "Sensor_3_Z_ETotal.DAT". These show the variation of the electric field along the X and Z axes, respectively.

The plot of variation of the electric field along the X-axis.

The plot of variation of the electric field along the Z-axis.

Immersing a Metallic Ellipsoid in the Uniform Field

With the PEC_3 group active in the navigation tree, draw a small ellipsoid according to the table below:

Part Name	Object Type	Material Type	Dimensions	Coordinates	Rotation Angles
Immerse	Ellipsoid	PEC_3	rx = 4mm, ry = 4mm, rz = 6mm	(0, 0, 0)	(0°, 0°, 0°)

To draw a ellipsoid, click the Ellipsoid button from the Object Toolbar or select the menu item Object → Solid → Ellipsoid .

Selecting the Ellipsoid tool in the object toolbar.

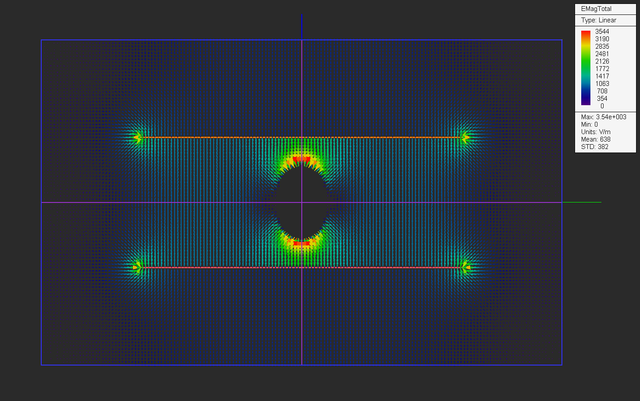
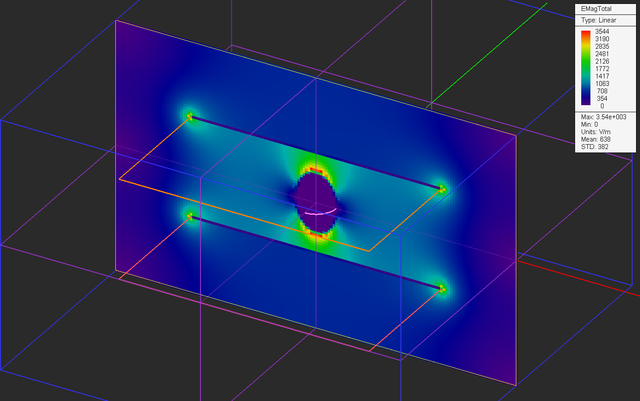
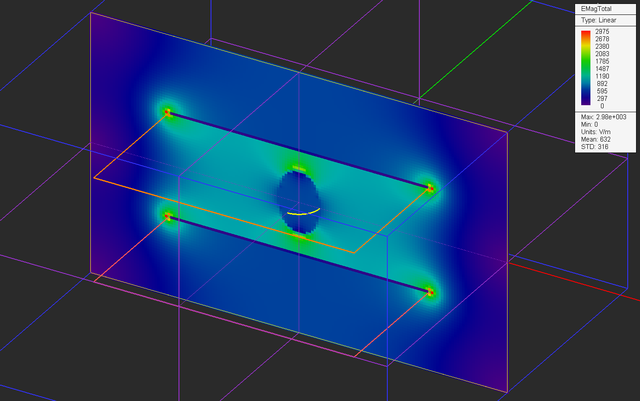
After drawing the PEC ellipsoid and placing it at the center of the gap region between the two metal plates, your physical structure should look like this:

The geometry of the two parallel metal plates and an immersed metallic ellipsoid.

Run an electrostatic analysis of your new structure and visualize the field distributions on the three sensor planes.

The electric field distribution in the Sensor_1 (XY) plane in the presence of the immersed PEC ellipsoid.

The electric field distribution in the Sensor_2 (YZ) plane in the presence of the immersed PEC ellipsoid.

The electric field distribution in the Sensor_3 (ZX) plane in the presence of the immersed PEC ellipsoid.

The figures below are the plots of the data files "Sensor_3_X_ETotal.DAT" and "Sensor_3_Z_ETotal.DAT". These show the variation of the electric field along the X and Z axes, respectively.

The plot of variation of the electric field along the X-axis in the presence of the immersed PEC ellipsoid.

The plot of variation of the electric field along the Z-axis in the presence of the immersed PEC ellipsoid.

Immersing a Lossy Dielectric Ellipsoid in the Uniform Field

Define a new dielectric material group called Dielectric_1 according to the table below:

Material Group	Material Type	εr	μr	σ	σm
Dielectric_1	Dielectric	4.0	1.0	100.0	0.0

Instead of deleting the PEC ellipsoid and drawing a new dielectric ellipsoid, you can simply move the object "Immerse" from the group "PEC_3" to the group "Dielectric_1". Follow the same procedure as you did in Tutorial Lesson 1 using the Move To items in the contextual menu of the spheroid object.

After drawing the PEC ellipsoid and placing it at the center of the gap region between the two metal plates, your physical structure should look like this:

The geometry of the two parallel metal plates and an immersed lossy dielectric ellipsoid. The top metal plate is in a freeze state.

Run an electrostatic analysis of your new structure and visualize the field distributions on the three sensor planes.

The electric field distribution in the Sensor_1 (XY) plane in the presence of the immersed lossy dielectric ellipsoid.

The electric field distribution in the Sensor_2 (YZ) plane in the presence of the immersed lossy dielectric ellipsoid.

The electric field distribution in the Sensor_3 (ZX) plane in the presence of the immersed lossy dielectric ellipsoid.

The figures below are the plots of the data files "Sensor_3_X_ETotal.DAT" and "Sensor_3_Z_ETotal.DAT". These show the variation of the electric field along the X and Z axes, respectively.

The plot of variation of the electric field along the X-axis in the presence of the immersed lossy dielectric ellipsoid.

The plot of variation of the electric field along the Z-axis in the presence of the immersed lossy dielectric ellipsoid.

Analyzing the Field Discontinuities

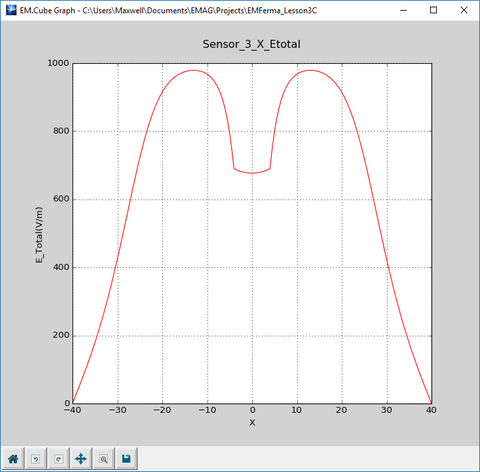
Let's take a look at the graphs of variation of the electric field along the X-axis in the three different cases you investigated above. In the first case without any immersed object, you see a uniform electric field of 1000V/m across the region between the two metal plates, which rolls off quickly in the outside free space region. In the second case with an immersed PEC ellipsoid, there is an actual null field at the center inside the ellipsoid. In the third case with an immersed dielectric ellipsoid, there is a non-zero field of a reduced amplitude.

Now look at the variation of the electric field along the Z-axis in the third case with the dielectric spheroid. There is a sharp discontinuity at Z = ±6mm, which represent the interfaces between the air and your dielectric material. This is expected as a result of the governing boundary conditions between two different dielectric materials. The boundary conditions require that:

[math] D_{n1} = D_{n2} [/math]

or

[math] \epsilon_{r1} E_{n1} = \epsilon_{r2} E_{n2} [/math]

In the case of your dielectric material, this means that

[math] \frac{E_{z1}}{E_{z2}} = 4 [/math]

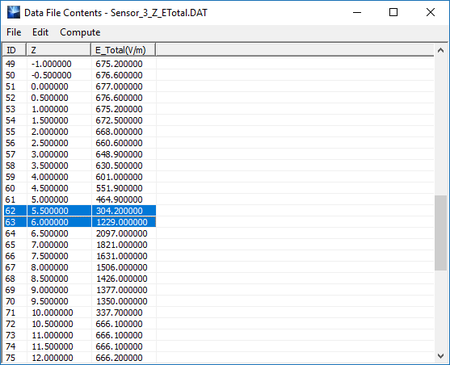
In the data manager, view the contents of the data file "Sensor_3_Z_ETotal.DAT" in the spreadsheet as shown below.

The contents of the data file "Sensor_3_Z_ETotal.DAT" shown in the data manager's spreadsheet.

Read the field values at the points below and above the dielectric-air interface. You can see that the computed ratio agrees well with the analytical result.

[math] \frac{E_{z1}}{E_{z2}} = \frac{|E(6mm)|}{|E(5.5mm)|} = \frac{1229.00}{304.20} = 4.04 [/math]

 

Back to the Top of the Page

Back to EM.Ferma Tutorial Gateway