Basic Electromagnetic Theory
![]() Back to Maxwell's Equations Page
Back to Maxwell's Equations Page
Contents
- 1 Electromagnetic Waves
- 2 Maxwell's Equations in Differential Form
- 3 The Wave Equations
- 4 Electric & Magnetic Boundary Conditions
- 5 Maxwell's Equations in Integral Form
- 6 Time-Harmonic Form of Maxwell's Equations
- 7 Electric and Magnetic Potentials
- 8 Green’s Function Representations
- 9 Free-Space Field Solutions
Electromagnetic Waves
An electromagnetic field is a physical field produced by electrically charged objects. The electromagnetic field can be viewed as the combination of an electric field and a magnetic field. The electric field is produced by stationary charges, while the magnetic field is produced by moving charges, i.e. electric currents. The electromagnetic field propagates indefinitely at the speed of light through a vacuum space. The oscillations of the two fields are perpendicular to each other and perpendicular to the direction of energy propagation, thus forming a propagating transverse wave.
The way in which charges and currents interact with the electromagnetic fields is described by Maxwell's equations.
Maxwell's Equations in Differential Form
Maxwell's equations form the basis for the mathematical formulation of almost all electromagnetic modeling problems. The differential form of Maxwell's equations relates the electric and magnetic fields and sources locally at every point in the space. In an isotropic, time-invariant and homogeneous medium, they are given by:
- [math] \nabla . \mathbf{D} = \rho [/math]
- [math] \nabla . \mathbf{B} = 0 [/math]
- [math] \nabla \times \mathbf{E} = - \dfrac{\partial \mathbf{B}}{\partial t} [/math]
- [math] \nabla \times \mathbf{H} = \dfrac{\partial \mathbf{D}}{\partial t} + \mathbf{J} [/math]
where ∇ is the gradient operator:
- [math] \nabla = \dfrac{\partial}{\partial x}\hat{\mathbf{x}} + \dfrac{\partial}{\partial y}\hat{\mathbf{y}} + \dfrac{\partial}{\partial z}\hat{\mathbf{z}} [/math]
∇. denotes the divergence operation, ∇× denotes the curl operation, E and H are the electric and magnetic fields in V/m and A/m, respectively, D and B are the electric and magnetic flux densities in C/m2 and Wb, respectively, J is the electric volume current density in A/m2, ρ is the electric volume charge density in C//m3, and the following constitutive relationships hold:
- [math] \mathbf{D} = \epsilon \mathbf{E}, \quad \quad \mathbf{B} = \mu \mathbf{H}, \quad \quad \mathbf{J} = \sigma \mathbf{E} [/math]
where ε is the permittivity in F/m, μ is the permeability in H/m, and σ is the electric conductivity of the medium in S/m.
Although real magnetic charges and currents do not exist in nature, using the electromagnetic equivalence theorem, it is convenient to introduce a magnetic volume charge density in C/m3, and a magnetic volume current density M in V/m2 to preserve the symmetry and duality of Maxwell's equations in the following form:
- [math] \nabla . \mathbf{D} = \rho [/math]
- [math] \nabla . \mathbf{B} = \rho_m [/math]
- [math] \nabla \times \mathbf{E} = - \dfrac{\partial \mathbf{B}}{\partial t} - \mathbf{M} [/math]
- [math] \nabla \times \mathbf{H} = \dfrac{\partial \mathbf{D}}{\partial t} + \mathbf{J} [/math]
The following constitutive relationships now hold:
- [math] \mathbf{D} = \epsilon \mathbf{E}, \quad \quad \mathbf{J} = \sigma \mathbf{E} [/math]
- [math] \mathbf{B} = \mu \mathbf{H}, \quad \quad \mathbf{M} = \sigma_m \mathbf{H} [/math]
where σm is the magnetic conductivity of the medium in Ω/m.
Additionally, one can write the following continuity equations:
- [math] \nabla . \mathbf{J} - \dfrac{\partial \rho}{\partial t} = 0 [/math]
- [math] \nabla . \mathbf{M} - \dfrac{\partial \rho_m}{\partial t} = 0 [/math]
The Wave Equations
Combining Maxwell's equations, we can arrive at the electric and magnetic wave equations:
- [math] \nabla^2 \mathbf{E} - \epsilon \mu \dfrac{\partial \mathbf{E}}{\partial t} = 0 [/math]
- [math] \nabla^2 \mathbf{H} - \epsilon \mu \dfrac{\partial \mathbf{H}}{\partial t} = 0 [/math]
where ∇2 is the Laplacian operator. The wave equations are hyperbolic partial differential equation in space coordinates and time, which must be solved subject to the proper initial and boundary conditions.
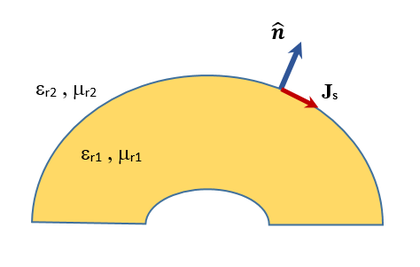
Electric & Magnetic Boundary Conditions
The electric field boundary conditions at the interface between two material media are:
[math] \hat{\mathbf{n}} . [ \mathbf{D_2(r)} - \mathbf{D_1(r)} ] = \rho_s (\mathbf{r}) [/math]
[math] \hat{\mathbf{n}} \times [ \mathbf{E_2(r)} - \mathbf{E_1(r)} ] = - \mathbf{M_s(r)} [/math]
where [math]\hat{\mathbf{n}}[/math] is the unit normal vector at the interface pointing from medium 1 towards medium 2, and ρs is the electric surface charge density, and Ms is the magnetic surface current density at the interface.
The magnetic field boundary conditions at the interface between two material media are:
[math] \hat{\mathbf{n}} . [ \mathbf{B_2(r)} - \mathbf{B_1(r)} ] = \rho_{ms} (\mathbf{r}) [/math]
[math] \hat{\mathbf{n}} \times [ \mathbf{H_2(r)} - \mathbf{H_1(r)} ] = \mathbf{J_s(r)} [/math]
where [math]\hat{\mathbf{n}}[/math] is the unit normal vector at the interface pointing from medium 1 towards medium 2, ρms is the magnetic surface charge density, and Js is the electric surface current density at the interface.
Maxwell's Equations in Integral Form
In certain applications, it is advantageous to cast Maxwell's equations in an integral form. These can be done using the theorems of vector calculus. In an isotropic, time-invariant and homogeneous medium, the integral forms of Maxwell's equations are given by:
- [math] \int\int_S \mathbf{D} . \mathbf{ds} = \int\int\int_V \rho dv [/math]
- [math] \int\int_S \mathbf{B} . \mathbf{ds} = \int\int\int_V \rho_m dv [/math]
- [math] \int_C \mathbf{E} . \mathbf{dl} = - \dfrac{\partial}{\partial t} \int\int_S \mathbf{B} . \mathbf{ds} - \int\int_S \mathbf{M} . \mathbf{ds} [/math]
- [math] \int_C \mathbf{H} . \mathbf{dl} = \dfrac{\partial}{\partial t} \int\int_S \mathbf{D} . \mathbf{ds} - \int\int_S \mathbf{J} . \mathbf{ds} [/math]
where V is a closed region of the space, S the surface boundary and C is a path.
Time-Harmonic Form of Maxwell's Equations
In a time-harmonic system operating at a given frequency f, the time dependence of the fields takes the form of [math] e^{j\omega t} [/math], where [math] j = \sqrt{-1} [/math], and ω = 2πf is the angular frequency. In that case, the time derivative is [math] {\partial}/{\partial t} = j\omega [/math], and Maxwell's curl equations reduce to:
- [math] \nabla \times \mathbf{E} = - j\omega \mathbf{B} - \mathbf{M} [/math]
- [math] \nabla \times \mathbf{H} = j\omega \mathbf{D} + \mathbf{J} [/math]
and the continuity equations reduce to:
- [math] \nabla . \mathbf{J} = j\omega \rho [/math]
- [math] \nabla . \mathbf{M} = j\omega \rho_m [/math]
The wave equations then reduce to the Helmholtz equations given by:
- [math] \nabla^2 \mathbf{E} + k^2 \mathbf{E} = 0 [/math]
- [math] \nabla^2 \mathbf{H} + k^2 \mathbf{H} = 0 [/math]
where [math] k = \omega \sqrt{\epsilon \mu} [/math] is the propagation constant in the medium.
Electric and Magnetic Potentials
Under the time-harmonic assumption, the electric and magnetic fields can further be expressed in terms of an electric scalar potential Φ, a magnetic scalar potential Ψ, a vector electric potential F and a vector magnetic potential A in the following form:
- [math] \mathbf{E(r)} = - \nabla \times \mathbf{F(r)} - \nabla \Phi(\mathbf{r}) - j\omega\mu \mathbf{A(r)} [/math]
- [math] \mathbf{H(r)} = \nabla \times \mathbf{A(r)} - \nabla \Psi(\mathbf{r}) - j\omega\epsilon \mathbf{F(r)} [/math]
with the additional gauge relations:
- [math] \nabla \times \mathbf{A(r)} = - j\omega\epsilon \Phi(\mathbf{r}) [/math]
- [math] \nabla \times \mathbf{F(r)} = - j\omega\mu \Psi(\mathbf{r}) [/math]
All the potential functions satisfy the Helmholtz equation:
- [math] \nabla^2 \mathbf{A} + k^2 \mathbf{A} = - \mathbf{J} [/math]
- [math] \nabla^2 \mathbf{F} + k^2 \mathbf{F} = - \mathbf{M} [/math]
- [math] \nabla^2 \Phi + k^2 \Phi = - \frac{\rho}{\epsilon} [/math]
- [math] \nabla^2 \Psi + k^2 \Psi = - \frac{\rho_m}{\mu} [/math]
Sometimes it is useful to define the Hertz vector potentials as:
- [math] \mathbf{\Pi_e} = \frac{1}{j\omega\epsilon} \mathbf{A(r)} [/math]
- [math] \mathbf{\Pi_m} = \frac{1}{j\omega\mu} \mathbf{F(r)} [/math]
In that case, the electric and magnetic fields can be fully expressed in terms of these two vector potentials:
- [math] \mathbf{E(r)} = -j\omega\mu \nabla \times \mathbf{\Pi_m} + k^2 \mathbf{\Pi_e} + \nabla \nabla . \mathbf{\Pi_e} [/math]
- [math] \mathbf{H(r)} = j\omega\epsilon\nabla \times \mathbf{\Pi_e} + k^2 \mathbf{\Pi_m} + \nabla \nabla . \mathbf{\Pi_m} [/math]
| |
For historical reasons, it is customary in electrostatic problems to directly set the magnetic flux density B equal to ∇ × A. EM.Cube's Static Module (EM.Ferma) uses that convention for definition of the vector magnetic potential A, which is different by a factor of μ from the definition of the A vector in the electrodynamic discussion presented in this section. That would also change the source term of the Helmholtz equation by the same factor. |
Green’s Function Representations
The Green’s functions are the analytical solutions of boundary value problems when they are excited by an elementary source. This is usually an infinitesimally small vectorial point source. The total electric (E) field and total magnetic (H) field can be expressed in terms of the volume electric current source J and volume magnetic current source M in the following way:
- [math] \mathbf{E = E^{inc}} + \mathbf{\iiint_{V_J} \overline{\overline{G}}_{EJ}(r|r') \cdot J(r') } d \nu' + \mathbf{\iiint_{V_M} \overline{\overline{G}}_{EM}(r|r') \cdot M(r') } d \nu' [/math]
- [math] \mathbf{H = H^{inc}} + \mathbf{\iiint_{V_J} \overline{\overline{G}}_{HJ}(r|r') \cdot J(r') } d \nu' + \mathbf{\iiint_{V_M} \overline{\overline{G}}_{HM}(r|r') \cdot M(r') } d \nu' [/math]
where Einc and Hinc are the incident electric and magnetic fields, respectively, and VJ and VM are the volumes containing the electric and magnetic current sources, respectively. The above equations involve four dyadic Green's functions types: dyadic electric-field Green’s functions due to electric current sources GEJ, dyadic magnetic-field Green’s functions due to electric current sources GHJ, dyadic electric-field Green’s functions due to magnetic current sources GEM, and dyadic magnetic-field Green’s functions due to magnetic current sources GHM . The incident or impressed fields represent the source terms and provide the excitation of the structure.
In order for the Green’s functions to be computationally useful, they must have analytical closed forms. This can be a mathematical expression or a more complex recursive process. It is no surprise that only very few electromagnetic boundary value problems have closed-form Green’s functions. Among EM.Cube's computational modules, EM.Libera is based on the free-space Green's functions, whereas EM.Picasso is based on the dyadic Green's functions of an arbitrary multilayer planar structure.
Free-Space Field Solutions
The simplest background structure is the unbounded free space, which is represented by the following Green’s function:
- [math] \mathbf{ \overline{\overline{G}}_{EJ}(r|r') = (\overline{\overline{I}} + \nabla\nabla) } G_{\Lambda} (\mathbf{r|r'}), \quad G_{\Lambda} (\mathbf{r|r'}) = \frac{ e^{-jk_0 \mathbf{|r-r'|}} }{ 4\pi \mathbf{|r-r'|} } [/math]
where [math]\mathbf{\overline{\overline{I}}}[/math] is the unit dyad, [math]\nabla[/math] is the gradient operator, r and r' are the position vectors of the observation and source points, respectively, and k0 is the free-space propagation constant. This implies that electromagnetic waves propagate in free space in a spherical form away from the source. Note that the Green’s function has a singularity at the source, i.e. when r = r'.
Assuming electric and magnetic surface current sources J and M residing on surfaces SJ and SM, respectively, the near-field equations reduce to:
- [math] \begin{align} \mathbf{ E(r) = E^{inc}(r) } & - jk_0 Z_0 \iint_{S_J} \left\{ \left[ 1 - \frac{j}{k_0 R} - \frac{1}{(k_0 R)^2} \right] \mathbf{J(r')} - \left[ 1 - \frac{3j}{k_0 R} - \frac{3}{(k_0 R)^2} \right] \mathbf{ (\hat{R} \cdot J(r')) \hat{R} } \right\} \frac{e^{-jk_0 R}}{4\pi R} ds' \\ & + jk_0 \iint_{S_M} \left[ 1-\frac{j}{k_0 R} \right] \mathbf{ (\hat{R} \times M(r')) } \frac{e^{-jk_0 R}}{4\pi R} ds' \end{align} [/math]
- [math] \begin{align} \mathbf{ H(r) = H^{inc}(r) } & - jk_0 Y_0 \iint_{S_M} \left\{ \left[ 1 - \frac{j}{k_0 R} - \frac{1}{(k_0 R)^2} \right] \mathbf{M(r')} - \left[ 1 - \frac{3j}{k_0 R} - \frac{3}{(k_0 R)^2} \right] \mathbf{ (\hat{R} \cdot M(r')) \hat{R} } \right\} \frac{e^{-jk_0 R}}{4\pi R} ds' \\ & - jk_0 \iint_{S_J} \left[ 1-\frac{j}{k_0 R} \right] \mathbf{ (\hat{R} \times J(r')) } \frac{e^{-jk_0 R}}{4\pi R} ds' \end{align} [/math]
where [math] R=|r-r'| \text{, } k_0 = \frac{2\pi}{\lambda_0} \text{ and } Z_0 = 1/Y_0 = \eta_0 [/math].