V&V Article 2: Computing Radar Cross Section Of Metallic Targets Using EM.Cube
Contents
- 1 Introduction
- 2 Scattering from a Small Metal Plate
- 3 Scattering from a Large Metal Plate
- 4 Scattering from a Metal Cube
- 5 Scattering from a Finite Metal Cylinder
- 6 Scattering from a Large Metal Sphere
- 7 Scattering from a Metal Cylindrical Rod with Rounded Ends
- 8 Scattering from a Long Metal Conesphere
- 9 References
Introduction
In this verification & validation (V&V) article, we will model electromagnetic scattering from a number of canonical targets and compute their radar cross section (RCS) using EM.Cube's different simulation engines. Each scattering problem will be solved using different EM.Cube solvers such as EM.Tempo's FDTD solver, EM.Libera's surface MOM solver and EM.Illumina's Physical Optics (PO) solver. The simulation results are compared against analytical and published simulation or measurement data.
Scattering from a Small Metal Plate
The first target to be simulated is a small thin metal (PEC) plate of dimensions 0.3λ0 × 0.3λ0, where λ0 is the free space wavelength. The backscatter RCS of this target is computed first using EM.Libera's Surface MoM simulation engine and then using EM.Tempo's FDTD engine. To calculate the backscatter RCS as a function of elevation angle θ, we ran an angular sweep of θ in both EM.Libera and EM.Tempo from θ = 180º (corresponding to a downward, normally incident, plane wave source) to θ = 90° (corresponding to a lateral, horizontally incident, plane wave source) with a step of 5 degrees. Figures 2 and 3 show the simulation results obtained using EM.Libera and EM.Tempo and compare them to the results obtained using the finite element method (FEM) given by Ref. [1]. Both theta (TMz) and phi (TEz) polarizations are considered, and the RCS results are plotted in Figures 2 and 3, respectively. Two sets of FDTD data are presented in these figures, one for a planar PEC square of zero thickness and one for a thin metal plate of thickness 0.01λ0. It can be seen that the infinitesimally thin planar object in FDTD predicts slightly larger RCS than the actual values.
 Figure 2: Variation of normalized back-scatter RCS (σ/λ2) of a thin metal square plate of dimensions 0.3λ0 × 0.3λ0 as a function of elevation angle θ for the case of an incident TMz (Eθ) polarization, solid red line: EM.Libera results, solid blue line: EM.Tempo results with a zero-thickness plate, solid green line: EM.Tempo results with a 0.01λ0 thick plate, magenta symbols: simulated data using the finite element method (FEM) presented by Ref. [1]. |
 Figure 3: Variation of normalized back-scatter RCS (σ/λ2) of a thin metal square plate of dimensions 0.3λ0 × 0.3λ0 as a function of elevation angle θ for the case of an incident TEz (Eφ) polarization, solid red line: EM.Libera results, solid blue line: EM.Tempo results with a zero-thickness plate, solid green line: EM.Tempo results with a 0.01λ0 thick plate, magenta symbols: simulated data using the finite element method (FEM) presented by Ref. [1]. |
Scattering from a Large Metal Plate
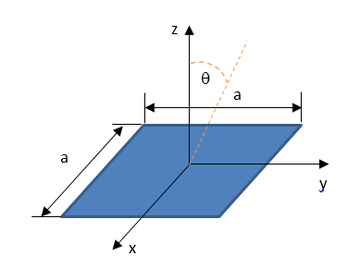
Next, we investigate the variation of RCS of a metal plate with its lateral size or frequency. For this purpose, we consider a thin metal (PEC) plate of dimensions a × a (same as shown in Figure 1), and compute its backscatter RCS as a function of k0a, where k0 = 2 π / λ0 = 2 π f / c. A plot of RCS vs. k0a shows the variation of RCS with frequency when the plate's lateral size a is fixed, or alternatively, the variation of RCS with the lateral dimension at a fixed frequency. Figure 4 shows the variation of the backscatter RCS of the square PEC plate with k0a as simulated by EM.Libera. These results are compared with measured data reported by Ref. [2]. Excellent agreement is observed between the two sets of data. The figure also shows the backscatter RCS data computed by EM.Illumina's Physical Optics (PO) solver. It is seen that the PO results do not agree well with the full-wave MoM results until the size of the plate grows to about a wavelength or more. This can also be interpreted as when frequency increases such that k0a > 6, which justifies the physical optics approximation.
 Figure 4: Variation of normalized back-scatter RCS (σ/λ2) of a thin metal square plate of dimensions a × a as a function of k0a (normalized plate length or normalized frequency) for the case of a normally incident plane wave source, solid red line: EM.Libera results, solid blue line: EM.Illumina (PO) results, magenta symbols: measured data referenced by Ref. [2]. |
The next example involves a large square metal (PEC) plate of dimensions 5λ0 × 5λ0 illuminated by an obliquely incident, plane wave source with θ = 30° measured from the zenith. For this electrically large plate, the physical optics method yields very good results at the main lobe and the first few side lobes. Figures 5 and 6 show the normalized bi-static RCS of the large plate as simulated by EM.Libera and EM.Illumina. The two figures correspond to the incident TMz and TEz polarizations, respectively. Note that the maximum RCS is observed at 30° as one would expect. At the grazing angles, one can see significant discrepancies between the asymptotic PO and full-wave Surface MoM results. For comparison, Figure 7 shows a reproduction of the physical optics results given by Ref. [3], which have been calculated analytically using a simple PO approximation of uniform surface currents on the metal plate.
 Figure 5: Variation of normalized bistatic RCS (σ/λ2) of a large metal square plate of dimensions 5λ0 × 5λ0 as a function of elevation angle θ for the case of an obliquely incident TMz polarization in the YZ plane (φs = 90°, 270°), solid red line: EM.Libera results, solid blue line: EM.Illumina (PO) results. |
 Figure 6: Variation of normalized bistatic RCS (σ/λ2) of a large metal square plate of dimensions 5λ0 × 5λ0 as a function of elevation angle θ for the case of an obliquely incident TEz polarization in the YZ plane (φs = 90°, 270°), solid red line: EM.Libera results, solid blue line: EM.Illumina (PO) results. |
Scattering from a Metal Cube
As the first volumetric target, we consider a metallic cube of dimensions a × a × a, illuminated by a normally incident, plane wave source. Similar to the metal plate case, we run a parametric sweep of EM.Libera and EM.Tempo with the cube length a defined as the sweep variable. We compute the backscatter RCS of the metallic cube as a function of k0a (normalized length or normalized frequency as you may interpret). Figure 8 shows the backscatter RCS results computed using EM.Libera and EM.Tempo and compares them with the published measured data given by Ref. [4]. Excellent agreement is observed among all three data sets.
 Figure 8: Variation of normalized back-scatter RCS (σ/λ2) of a metal cube of dimensions a × a × a as a function of k0a (normalized cube dimension or normalized frequency) for the case of a normally incident plane wave source, solid red line: EM.Libera results, solid blue line: EM.Tempo results, magenta symbols: measured data given by Ref. [4]. |
Scattering from a Finite Metal Cylinder
The next volumteric target to be considered is a finite metallic cylinder with an equal height and diameter of 0.6λ0. Figures 9 and 10 show the triangular surface mesh and Yee voxel mesh of this target illuminated by a normally incident plane wave source. The backscatter RCS of this target is computed first using EM.Libera's surface MOM simulation engine and then using EM.Tempo's FDTD solver. Figures 11 and 12 show the simulation results obtained using EM.Libera and EM.Tempo and compare them to the results obtained using the finite element method (FEM) given by Ref. [5]. The figures correspond to the theta (TMz) and phi (TEz) polarizations, respectively. Excellent agreement is observed among the three data sets for both polarizations.
 Figure 11: Variation of normalized back-scatter RCS (σ/λ2) of a finite metallic cylinder with an equal height and diameter square plate of 0.6λ0 as a function of elevation angle θ for the case of an incident TMz (Eθ) polarization, solid red line: EM.Libera results, solid blue line: EM.Tempo results, magenta symbols: simulated data using the finite element method (FEM) presented by Ref. [5]. |
 Figure 12: Variation of normalized back-scatter RCS (σ/λ2) of a finite metallic cylinder with an equal height and diameter square plate of 0.6λ0 as a function of elevation angle θ for the case of an incident TEz (Eφ) polarization, solid red line: EM.Libera results, solid blue line: EM.Tempo results, magenta symbols: simulated data using the finite element method (FEM) presented by Ref. [5]. |
Scattering from a Large Metal Sphere
Next, we examine scattering from a large metallic sphere. For this case, we consider a PEC sphere of radius 477.465 mm corresponding to k0a = 10, at the frequency f = 1GHz. Figure 13 shows the triangular surface mesh of this sphere generated by the EM.Libera or EM.Illumina mesh generators. A mesh density of 100 samples/λ02 has been used for this mesh. Figures 14 and 15 show the bistatic RCS of the metallic sphere as a function of the elevation angle θ for the two cases of TMz and TEz polarizations, respectively. The two figures compare the results computed by EM.Libera's surface MOM solver and EM.Illumina's Physical Optics (PO) solverand compare them with the simulated results given by Ref. [6], which presents two sets of data, one based on the method of moments (MoM) and the other based on a hybrid PO/MoM/Fock technique. The two data sets in Ref. [6] are almost identical. Like in the previous example, physical optics predicts the RCS over the main beam (or maximum RCS angles) adequately; however, its accuracy degrades over the side lobes.EM.Libera's results almost exactly match those of Ref. [6].
 Figure 14: Variation of normalized bistatic RCS (σ/λ2) of a large metallic sphere of radius a (k0a = 10) with elevation angle θ for the case of an incident TMz (vertical) polarization, solid red line: EM.Libera results, solid blue line: EM.Illumina (PO) results, magenta symbols: simulated data using a hybrid PO/MoM/Fock method presented by Ref. [6]. |
 Figure 15: Variation of normalized bistatic RCS (σ/λ2) of a large metallic sphere of radius a (k0a = 10) with elevation angle θ for the case of an incident TEz (horizontal) polarization, solid red line: EM.Libera results, solid blue line: EM.Illumina (PO) results, magenta symbols: simulated data using a hybrid PO/MoM/Fock method presented by Ref. [6]. |
Scattering from a Metal Cylindrical Rod with Rounded Ends
Figure 16 shows the geometry of a metallic cylindrical rod with rounded (hemispherical) ends. The total end-to-end length of the rod is 1.5λ0, and its diameter is 0.4λ0. This structure was simulated using EM.Libera and EM.Tempo. Figures 17 and 18 show the triangular surface mesh and the FDTD mesh of the same structure, respectively. For the surface mesh generation, a mesh density of 225 samples/λ02 was used, while the FDTD module used a mesh density of 25 cells/λeff along each linear dimension with high precision adaptive mesh contour settings to better capture the curved surface of the target.
Figures 19 and 20 show the computed bistatic RCS of the cylindrical rod as a function of the elevation angle when the target is illuminated from the bottom by a normally incident plane wave source. The two figures correspond to the bistatic RCS in the two principal planes YZ (φ = 90°) and ZX (φ = 0°), respectively. These figures compare the results simulated by EM.Libera and EM.Tempo with those reported in Ref. [7] based on a method of moments (MOM) formulation of bodies of revolution (BOR).
 Figure 19: Variation of normalized bistatic RCS (σ/λ2) of a metallic cylindrical rod with rounded ends as a function of elevation angle θ in YZ plane (φ = 90°), solid red line: EM.Libera results, solid blue line: EM.Tempo results, magenta symbols: simulated data using a BOR-MoM method presented by Ref. [7]. |
 Figure 20: Variation of normalized bistatic RCS (σ/λ2) of a metallic cylindrical rod with rounded ends as a function of elevation angle θ in ZX plane (φ = 0°), solid red line: EM.Libera results, solid blue line: EM.Tempo results, magenta symbols: simulated data using a BOR-MoM method presented by Ref. [7]. |
Scattering from a Long Metal Conesphere
The last metallic volumetric target to be considered is a long conesphere as shown in Figure 21. The diameter of the sphere is 0.94λ0, and the total end-to-end length of the target from the apex of the cone to the bottom of the sphere is 3.137λ0. This structure was simulated using EM.LIbera and EM.Tempo. Figure 22 shows the triangular surface mesh of the target with a mesh density of 225 samples/λ02. Figure 23 shows the FDTD mesh of the same structure with a mesh density of 25 cells/λeff along each linear dimension together with high precision adaptive mesh contour settings.
Figures 24 and 25 show the bistatic RCS results for the metallic conesphere illuminated from the top (apex) by a normally incident plane wave source with TMz (vertical) and TEz (horizontal) polarizations, respectively. Both figures show and compare the results generated by EM.Libera and EM.Tempo. To avoid overlapping figures, Figure 26 shows the corresponding results for the same target given by Ref. [6], where three data sets are compared: one using the standard MoM (similar to EM.Libera), plus two other hybrid PO/MoM and Fock/MoM methods. Very good agreement is observed among the published data and EM.Cube's results.
References
[1] J. Jin, The Finite Element Method in Electromagnetics. Chapter 8, pp. 275-277, John Wiley & Sons, 1993.
[2] S.M. Rao, D.R. Wilton, and A.W. Glisson, “Electromagnetic scattering by surface of arbitrary shape,” IEEE Trans. on Antennas & Propagat, Vol. 30, No. 3, pp. 107-116, 1982.
[3] C.A. Balanis, Advanced Engineering Electromagnetics. Chapter 11, pp. 591-599, John Wiley & Sons, 2012.
[4] R.P. Penno, G.A. Thiele, and K.M. Pasala, “Scattering from a perfectly conducting cube,” Proc. IEEE, Vol. 77, pp. 815-823, 1989.
[5] A. Chatterjee, J.M. Jin and J. L. Volakis, "Edge-based finite elements and vector ABC's applied to 3-D scattering," IEEE Trans. on Antennas & Propagat, Vol. 41, No. 2, pp.221-226, 1993.
[6] L.N. Medgyesi-Mitschang and D-S Wang, “Hybrid solutions for scattering from perfectly conducting bodies of revolution,” IEEE Trans. on Antennas & Propagat, Vol. 31, No. 4, pp. 570-583, 1983.
[7] M.G. Andreasen, “Scattering from bodies of revolution,” IEEE Trans. on Antennas & Propagat, Vol. 13, No. 2, pp. 303-310, 1965.