EM.Picasso Tutorial Lesson 10: Optimizing A Microstrip Patch Antenna Design
Contents
What You Will Learn
In this tutorial you will revisit the rectangular patch antenna design with a recessed feed, which you explored earlier in Tutorial Lesson 2. This time, however, you will define a design objective and will use EM.Picasso's optimization utility to optimize the values of designated design variables to achieve your goal.
Back to EM.Picasso Tutorial Gateway
Download projects related to this tutorial lesson
Getting Started
Open the EM.Cube application and switch to EM.Picasso. Start a new project with the following parameters:
Creating the Patch Geometry with a Recessed Feed
Follow a similar procedure as in Tutorial Lesson 2 and use the Microstrip-Fed Patch Wizard to create the parameterized geometry of a patch antenna with a recessed feed.
 |
Open the variables dialog and make the following changes:
| Variable Name | Original Definition | New Definition |
|---|---|---|
| patch_len | floor(0.5*lambda0_unit*100/sqrt(er))/100 | 42 |
| recess_dep | 0.015*to_meters | 15 |
| recess_wid | 0.005*to_meters | 5 |
 |
Defining the Design Objective
In this project, you will fix the side dimensions of the patch ("patch_len"), and will optimize the two feed variables: "recess_dep" and "recess_wid". But first you need to define a design objective for your project. The goal here is to achieve a good impedance match by varying the design variables. A return loss of -20dB typically represents a very good impedance match.
To define a design objective, click on the Objectives 
button of the Simulate Toolbar or select the menu item Simulate → Objectives... EM.Cube's Objectives dialog opens up, which is initially empty.
 |
Click the Add button of this dialog to open "Add Objective" dialog. At the bottom of this dialog you will see a list of EM.Cube's available standard output parameters. The contents of this list vary depending on the observables you have already defined for your project. Since the wizard created a port definition for this project, you will see a number of standard output parameters related to the S/Z/Y parameters. A design objective is defined as a logical statement:
expression_1 logical operator expression_2
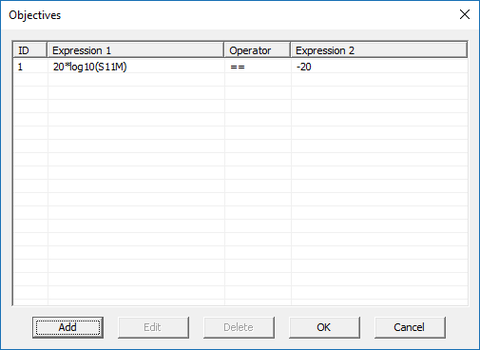
The first and second expressions can be any mathematical expression involving the standard output parameters, variables, Python functions, etc. The logical operators are "==", "<", "<=", ">", ">=" and "!=" (Not Equal To). If you set the mouse focus at one of the expression boxes and then double-click on the name of one of the output parameters in the list, it will be inserted in that box. Set up the following design objective as shown in the figure below:
20*log10(S11M) == -20
 |
Close the "Add Objective" dialog to return to the Objectives dialog. You will see your new design objective added to the current objectives list. Close this dialog, too, and return to the project workspace.
 |
Setting Up the Optimization Process
Open the simulation run dialog and select Optimization from the drop-down list labeled Simulation Mode.
 |
Click the Settings button next to this drop-down list to open the Optimization Settings dialog.
 |
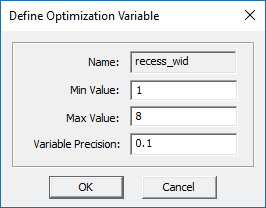
Keep the default optimization Algorithm Type, which is "Powell's Method". Next, you need to define the optimization variables. Similar to the case of a parametric sweep, on the left side of the dialog you will see a list of all the available independent variables already defined in your project. Select and highlight "recess_dep" and click the right arrow --> button in the middle of the dialog to move the selected variable to the Optimization Variables list on the right. A new dialog titled "Edit Optimization Variable" opens up. Enter 2 and 16 for the minimum and maximum values, respectively. Keep the default Variable Precision value of 0.1. Similarly, move "recess_wid" to the optimization variables table and enter 1 and 8 for its minimum and maximum values, respectively.
 |
 |
Back in the optimization settings dialog, you will see the specifications of the two optimization variables in the table on the right. Set the value of Max Error equal to 0.1. This is used for the convergence of the objective function or error function. You can see from the figure below that the error function or "goal" has been defined by the mathematical expression:
| (20*log10(S11M)) - (-20) |
 |
Running the Optimization of the Patch Antenna
Run the simulation and wait until the optimization algorithm converges. Note that sometimes the optimization process may never converge. This means that the goal you have set for your optimization might never be achieved within the defined range of the optimization variables. In that case, the optimization algorithm will complete the specified maximum number of iterations and will exit the loop. If the optimization is successful, EM.Cube automatically changes the values of the optimization variables and sets them equal to their optimal values. In this project, the Powell optimization algorithm yields the following optimal values for the designated design variables:
| Design Variable Name | Optimal Value |
|---|---|
| recess_dep | 13.1384 |
| recess_wid | 2.02129 |
 |
 |
Verifying Your Optimized Patch Design
To verify the outcome of your optimization process, run a Single-Frequency Analysis of your patch structure at the project center frequency of fc = 2.4GHz. After the completion of the simulation, the output message window reports the port characteristics of your new optimized antenna:
S11: -0.060578 -0.077976j
S11(dB): -20.109976
Z11: 43.781258 -6.894998j
Y11: 0.022288 +0.003510j
As you can see from the value of the return loss, the specified design goal has been accomplished.
