Application Note 4: Modeling Large Parabolic Reflectors Illuminated By Pyramidal Horn Antennas Using EM.Cube
Contents
Introduction
Parabolic reflectors are typically used as high-gain antenna due to their electrically very large aperture dimensions. The Physical Optics (PO) technique can solve reflector problems efficiently when the details of the feed mechanism can be neglected. For example, a parabolic reflector with a very large focal length can be modeled using a Hertzian short dipole radiator placed at its focal point. Besides the conventional Geometrical-Optics-Physical-Optics (GOPO) technique, EM.Illumina (EM.Cube's PO Module) offers a generalized Iterative Physical Optics (IPO) solver. IPO effectively compensates for the shortcomings of GOPO with regard to multiple shadowing effects and handling of concave surfaces that support multi-bounce rays. Therefore, IPO is a good candidate for solving large parabolic reflector antenna structures. The basic steps of simulating a parabolic reflector antenna using the IPO solver are described in detail in EM.Illumina Tutorial Lesson 3: Computing The Radiation Pattern Of Parabolic Dish Reflectors.
In many realistic situations, however, the reflector's feed structure cannot be approximated as a simple point source or it may even cause blocking effects. In problems like this, a full-wave simulation of the entire structure is needed. In this application note, first we investigate the radiation characteristics of a large X-band parabolic reflector at 10GHz using EM.Illumina. Then, we add a realistic pyramidal horn feed to the reflector and simulate the combination antenna using EM.Tempo's full-wave FDTD solver.
A Note on Parabolic Reflectors
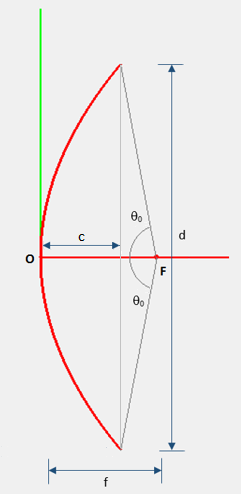
The geometry of a parabola is shown in the figure below. The parabola has a focal length of f, an axial length (depth) of c and an aperture diameter of d. The subtended angle θ0 is calculated from the following formula given by Ref. [1]:
[math] \cot \left( \frac{\theta_0}{2} \right) = 4 \left( \frac{f}{d} \right) [/math]
The ratio of the focal point to diameter f/d is a very important design parameter of parabolic reflectors. Furthermore, it can be shown that
[math] d^2 = 16fc [/math]
EM.Cube has a parabolic reflector wizard that creates a parameterized paraboloid characterized by two parameters "focal_length" and "axial_length". The diameter of the reflector can be determined from the above equation.
Ref. [1] derives an extensive set of equations for calculating the directivity of a parabolic reflector. These equations can be summarized as:
[math] D_0 = \epsilon_{ap} \left( \frac{\pi d}{\lambda_0} \right)^2 [/math]
where λ0 is the free-space wavelength, εap is the aperture efficiency given by:
[math] \epsilon_{ap} = \cot^2 \left( \frac{\theta_0}{2} \right) \left| \int_0^{\theta_0} \sqrt{G_f(\theta^{\prime})} \tan \left( \frac{\theta^{\prime}}{2} \right) d\theta^{\prime} \right|^2 [/math]
and Gf(θ) is the primary feed pattern function.
If the parabolic reflector is illuminated by an ideal point source at its focal point, it can be shown that the primary feed pattern function reduces to:
[math] G_f(\theta) = \sec^4 \left( \frac{\theta}{2} \right), \quad \theta \le \theta_0 [/math]
In that case, one can find an analytical expression for the aperture efficiency:
[math] \epsilon_{ap} = \tan^2 \left( \frac{\theta_0}{2} \right) [/math]
Initial Physical Optics Analysis of the Parabolic Reflector
For this project, first we consider an X-band parabolic reflector with the following specifications:
| Parameter Name | Value | Electrical Dimension |
|---|---|---|
| Focal Length (f) | 240mm | 8λ0 |
| Axial Length (c) | 60mm | 2λ0 |
| Aperture Diameter (d) | 480mm | 16λ0 |
| f/d Ratio | 0.5 | N/A |
| Subtended Angle (θ0) | 53.13° | N/A |
| Estimated Aperture Efficiency (εap) | 0.25 | N/A |
| Estimated Directivity (D0) | 28dB | N/A |
The operating frequency is f = 10GHz and the free-space wavelength at this frequency is λ0 = 30mm. This is a fairly large reflector that can be analyzed using EM.Illumina's IPO solver. We place a Y-directed Hertzian short dipole radiator at the focal point of this reflector to excite it. The figure below shows the geometry setup in EM.Illumina.
The surface of the reflector is discretized using a triangular surface mesh generator with a mesh density of 10 cells per wavelength along each linear direction. On the average, this creates about 230 cells per square wavelength. In the case of the above parabolic reflector, a total of 50,342 triangular cells are generated as shown in the figure below.
EM.Illumina' IPO solver is highly parallelized for multi-core CPU architectures. The IPO simulation was performed on an ASUS laptop computer with an Intel i7-4860 HQ processor with eight cores. The laptop features 32GB RAM memory. The entire simulation takes 254 seconds. This includes the two IPO iterations and computation of the full 3D far-field radiation pattern at angular resolution of 1° along both azimuth and elevation. The figures below show the surface electric current distribution on the parabolic reflector and its 3D radiation pattern. The computed directivity is 27.9dB, which agrees very well with the estimated analytical value.
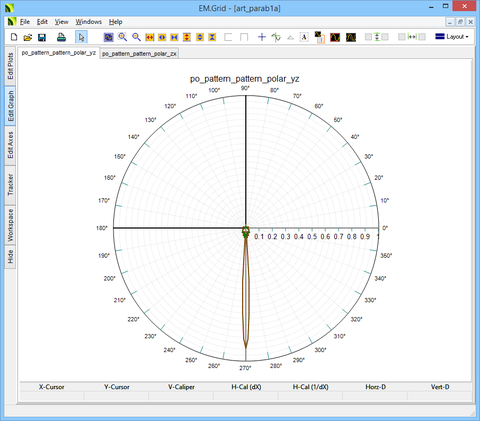
The figures below show the 2D polar radiation patterns of the parabolic reflector in the principal E and H planes.
The figures below show the 2D Cartesian radiation patterns of the parabolic reflector in the principal E and H planes.
Examining the Pyramidal Horn Feed
As a real feed mechanism, we will next consider a waveguide-fed pyramidal horn antenna. EM.Cube provides a convenient horn wizard that creates the geometry of a pyramidal horn antenna with a rectangular waveguide feed. The waveguide feed has a short plate at its other end. The basic steps of constructing and analyzing a pyramidal horn antenna are discussed in detail in EM.Tempo Tutorial Lesson 7: Designing A Pyramidal Horn Antenna.
In this project, the waveguide feed is a standard WR-90 hollow rectangular waveguide with an operational frequency bandwidth of 8.2GHz - 12.4GHz. The waveguide supports the dominant TE10 mode within this frequency range. The wizard calculates the aperture dimensions and length of the horn for a given directivity value. The default value of the directivity is 15dB. The table below shows the various parameters including the dimensions of the horn calculated by the wizard:
| Design Variable Name | Value |
|---|---|
| wg_a | 22.86mm |
| wg_b | 10.16mm |
| wg_l | 30mm |
| wg_off | 10mm |
| gain_dB | 15dB |
| horn_aperture_a | 77.35mm |
| horn_aperture_b | 57.15mm |
| horn_len | 38.13mm |
The figure below shows the geometry setup for the horn antenna in EM.Tempo.
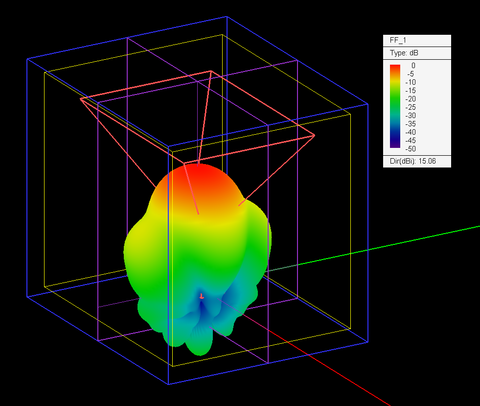
We ran an FDTD simulation of the horn structure in EM.Tempo to verify the design goal of a directivity of 15dB. The figure below shows the 3D radiation pattern of the horn antenna with a computed directivity of D0 = 15.06dB.
Analyzing the Reflector-Horn Combination Antenna Using EM.Tempo
Now we place the pyramidal horn antenna such that the horn aperture is aligned at the focal point of the large parabolic reflector as shown in the figure below.
This is a very large computational problem with a domain size of about 17λ0 × 17λ0 × 11λ0. The computational domain is terminated in convolutional perfectly matched layers (PML) from all six sides. To keep the simulation manageable, a mesh density of 15 cells per effective wavelength is adopted. EM.Tempo's mesh generator uses an initial tessellation of the physical structure to accelerate the Yee mesh generation. To get a smooth mesh of the curved surface of the paraboloid, a curved edge angle tolerance of 10° is used. A very large FDTD grid (550 x 548 x 350) is generated. The Yee mesh of the reflector-horn combination is shown in the figure below.
The FDTD simulation was run on the same ASUS laptop computer. The simulation involved a total of 105,490,000 Total cells and converged after 8,850 time steps. The total simulation time was 155 minutes including both the FDTD time marching loop and computation of the full 3D far-field radiation pattern at a resolution of 1° along both the azimuth and elevation directions.
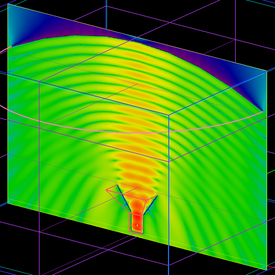
First, we consider the electric field distributions at four planes: two vertical E and H planes coincident with the principal YZ and ZX planes, respectively, and two horizontal planes, one on the reflector aperture and the other slightly above the horn aperture.
The figure below shows the dB-scale 3D far-field radiation pattern of the parabolic reflector with the pyramidal horn feed. As you can see from the figure, the value of the directivity has not changed significantly from the previous case due to the presence of the horn feed. However, the perfect circular symmetry of the pattern in the case of the short dipole feed is now all but gone.
The figures below show the 2D polar radiation patterns of the parabolic reflector with the pyramidal horn feed in the principal E and H planes.
The figures below show the 2D Cartesian radiation patterns of the parabolic reflector in the principal E and H planes.
Simulating a Larger Parabolic Reflector
In the last part of this application note, we consider a much larger parabolic reflector. For this purpose, we use the same pyramidal horn feed of the previous section. We also keep the axial length fixed and increase the focal length by 1.5 times to 12λ0. The f/d ratio now increases to 0.612. The dimensions of the combination structure are summarized in the table below.
| Parameter Name | Value | Electrical Dimension |
|---|---|---|
| Focal Length (f) | 360mm | 12λ0 |
| Axial Length (c) | 60mm | 2λ0 |
| Aperture Diameter (d) | 587.88mm | 19.6λ0 |
| f/d Ratio | 0.612 | N/A |
| wg_a | 22.86mm | 0.762λ0 |
| wg_b | 10.16mm | 0.339λ0 |
| wg_l | 30mm | λ0 |
| wg_off | 10mm | 0.333λ0 |
| horn_aperture_a | 77.35mm | 2.578λ0 |
| horn_aperture_b | 57.15mm | 1.905λ0 |
| horn_len | 38.13mm | 1.271λ0 |
The figure below shows the geometry setup for the larger parabolic reflector in EM.Tempo.
The size of the computational domain in this case is about 20λ0 × 20λ0 × 15λ0. Using the same mesh density of 15 cells per effective wavelength, a very large FDTD grid (636 x 632 x 443) is generated with a total of 178,064,736 cells. The FDTD simulation was run on the same ASUS laptop computer and converged after 9,275 time steps. The total simulation time was 235 minutes including both the FDTD time marching loop and computation of the high-resolution 3D far-field radiation pattern.
The figure below shows the dB-scale 3D far-field radiation pattern of the larger parabolic reflector with the pyramidal horn feed. As you can see from the figure, the value of the directivity has increased by 3.35dB compared to the reflector of the previous case with the smaller aperture size. Moreover, the main beam exhibits a better symmetry in the principal planes.
The figures below show the 2D polar radiation patterns of the larger parabolic reflector in the principal E and H planes.
The figures below show the 2D Cartesian radiation patterns of the larger parabolic reflector in the principal E and H planes.
References
[1] C.A. Balanis, Antenna Theory Analysis and Design. Chapter 15, Wiely Interscience, 3rd. Edition, 2005.