RF Tutorial Lesson 9: Impedance Matching Using Tuning Stubs
Contents
- 1 Objective
- 2 Tuning Stubs: An Overview
- 3 Single-Stub Impedance Matching Using a Series Open Stub
- 4 A Summary of Series Stub Matching Theory
- 5 Single-Stub Impedance Matching Using a Shunt Short Stub
- 6 A Summary of Shunt Stub Matching Theory
- 7 Double-Stub Impedance Matching Using Two Open Stubs
- 8 A Summary of Double Stub Matching Theory
Objective
In this tutorial, you will continue to use the transmission line circuits of the previous tutorial lesson with inductive and capacitive loading. For the inductive load, you will design a single-stub matching network using a series open stub. For the capacitive load, you will first design a single-stub matching network using a parallel short stub and then will design a double-stub matching network using two parallel open stubs.
Tuning Stubs: An Overview
Impedance matching is one of the most important aspects of RF circuit design. The purpose of impedance matching is to connect an arbitrary complex-valued load impedance to a source with a given resistive internal impedance (usually 50Ω) without causing input reflection and to ensure maximum power transfer from the source to the load. In many other cases, the given load needs to be impedance-matched to a transmission line of given characteristic impedance. Tuning stubs are segments of open-ended or short-ended transmission lines that are used for distributed impedance matching. Both open and short stubs can be used for impedance matching. From the transmission line theory, we know that open and short stubs have a pure imaginary input impedance.
There are single-stub and double-stub matching network designs:
- In a single-stub design, you insert a T-Line segment of length L between the source and load such that the input impedance looking into the T-Line from the point of view of the source has a real part equal to the source resistance. Then you use an open or short stub either in a series or parallel configuration to cancel the imaginary part of the input impedance.
- In a double-stub matching network, a tuning stub is placed at the location of the load and another one is placed at a distance of λg/8 from the first stub towards the source. The length of the first stub is chosen such that the combination of the load and first stub moves to the 1+jb circle. The combination load is then rotated along the constant VSWR circle by π/2 towards the source until you intersect the unit r = 1 circle. The length of the second stub is chosen to move you to the center of the Smith chart.
 |
 |
Single-Stub Impedance Matching Using a Series Open Stub
Additional parts you need for this part of the tutorial lesson:
- A Generic T-Line (Keyboard Shortcut: T)
- A Generic Open Stub
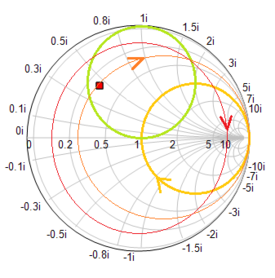
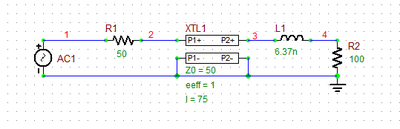
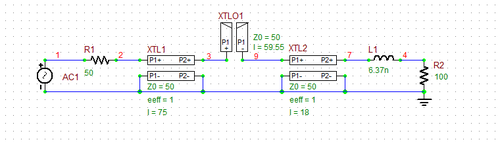
The following figure on the left shows the original transmission line circuit of RF Tutorial Lesson 2 with an inductive loading. Suppose the source circuit consists of the voltage source, the source series resistor and the 75mm, 50Ω transmission line segment. We want to design a matching network between the source circuit and the inductive load of 100 + j80 Ohms at f = 2GHz. The figure on the right shows a series open stub placed at a distance from the load through a segment of a 50Ω T-Line. When the length of the connecting (spacer) T-Line is chosen to be 18mm and the length of the open stub is chosen to be 59.55mm, the input impedance looking into the combination of the stub and the load to the right becomes 50Ω.
 |
 |
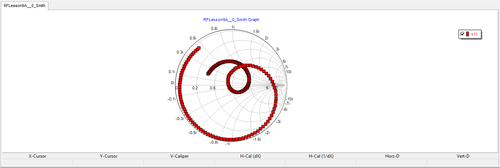
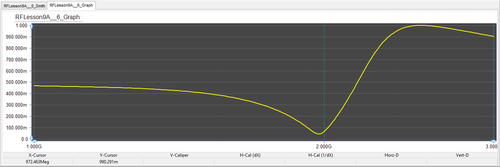
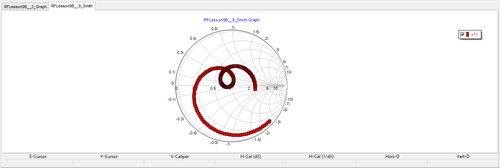
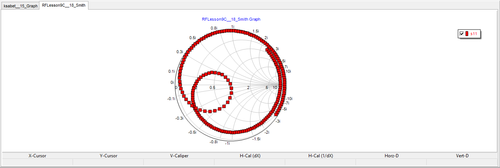
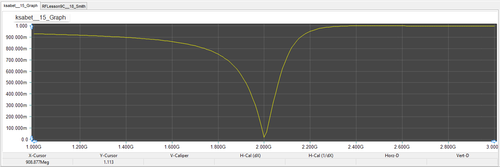
To verify this, run a network analysis of the circuit with the tuning stub matching network. Use Node 2 as the input port. Plot the s11 data on the Smith chart. Use the same start and stop frequencies as in the previous tutorial lesson, i.e. 1GHz and 3GHz, respectively, with a step size of 100MHz. You can see from the figure below that at f = 2GHz, the plot passes through the center of the Smith chart. It would be informative to plot the return loss, i.e. |s11| as a function of frequency on a Cartesian graph. In the Output tab of the Network Analysis Test Panel, choose "Cartesian (Amplitude)" as the graph type. To obtain a smooth curve, set the frequency step size to 10MHz. The results are depicted in the figure below, showing a vanishing return loss at 2GHz.
 |
 |
A Summary of Series Stub Matching Theory
The design of the series tuning stub utilized in the previous part is now explained. Let the load admittance be YL = 1 / ZL = GL + j BL. The admittance looking into a T-Line segment of length d terminated by the load YL is given by:
[math]Y_{in} = Y_0 \frac{ \left(G_L + j B_L \right) + jY_0 t}{Y_0 + j \left( G_L + j B_L \right) t}[/math]
where t = tan (β d). The impedance at this point can then be written as:
[math]Z_{in} = \frac{1}{Y_{in}} = R_{in} + j X_{in} = \frac {G_L ( 1+ t^2)}{G_L^2+(B_L + Y_0 t)^2} + j \frac {G_L^2 t - (Y_0 - B_L t)(B_L + Y_0 t)}{Y_0 \left[ G_L^2+(B_L + Y_0 t)^2 \right]} [/math]
Now we choose the T-Line segment length d such that Rin = Z0. This results in a quadratic equation for t:
[math] Y_0(G_L - Y_0)t^2 -2B_L Y_0 t + (G_L Y_0 t -G_L^2 -B_L^2) = 0 [/math]
which can be solved for t. In the special case GL = Y0, there is one solution t = -BL / 2Y0. Otherwise, two distinct roots for t are found. Once t is found, the segment length can be calculated by solving t = tan (2π d / λg).
The stub reactance X is chosen such that X = -Xin. From this condition, you can find the length of the stub depending on whether you use a short or open stub. Recall that the impedance of an open-ended or shorted transmission line segment of length L is given by:
[math] Z_{open} = -jZ_0 cot(\beta L) [/math]
and
[math] Z_{short} = jZ_0 tan(\beta L) [/math]
Therefore, the equations for the length Ls of the open stub or short stub are given by:
[math] X_{open} = -Z_0 cot (2\pi L_s / \lambda_g) = -X_{in} [/math]
[math] X_{short} = Z_0 tan (2\pi L_s / \lambda_g) = -X_{in} [/math]
 |
When running a network analysis of a large interconnected circuit, you can easily change the port nodes and find the impedance/admittance or reflection coefficient looking into any segment of your circuit. Table data usually prove more useful than graphs in such cases. |
Single-Stub Impedance Matching Using a Shunt Short Stub
Additional parts you need for this part of the tutorial lesson:
- A Generic T-Line (Keyboard Shortcut: T)
- A Generic Short Stub
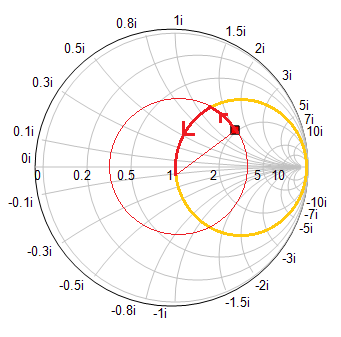
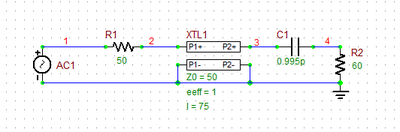
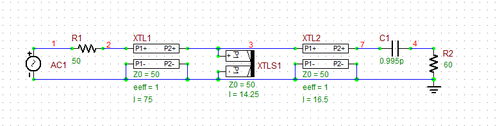
The following figure on the left shows the original transmission line circuit of RF Tutorial Lesson 2 with a capacitive loading. This time, you will design a matching network between the source circuit and the capacitive load of 60 - j80 Ohms at f = 2GHz. The figure on the right shows a parallel short stub placed at a distance from the load through a segment of a 50Ω T-Line. When the length of the connecting (spacer) T-Line is chosen to be 16.5mm and the length of the short stub is chosen to be 14.25mm, the input impedance looking into the combination of the stub and the load to the right becomes 50Ω.
 |
 |
Now run a network analysis of the circuit with the tuning stub matching network. Use Node 2 again as the input port. Plot the s11 data on the Smith chart with a frequency step size of 100MHz and then plot the return loss (|s11|) on a Cartesian graph with a frequency step size of 10MHz. The results are shown in the figures below.
 |
 |
A Summary of Shunt Stub Matching Theory
The design of the shunt tuning stub utilized in the previous part is now explained. Let the load impedance be ZL = 1 / YL = RL + j XL. The impedance looking into a T-Line segment of length d terminated by the load ZL is given by:
[math]Z_{in} = Z_0 \frac{ \left(R_L + j X_L \right) + jZ_0 t}{Z_0 + j \left(R_L + j X_L \right) t}[/math]
where t = tan (β d). The admittance at this point can then be written as:
[math]Y_{in} = \frac{1}{Z_{in}} = G_{in} + j B_{in} = \frac {R_L ( 1+ t^2)} {R_L^2+(X_L + Z_0 t)^2} + j \frac {R_L^2 t - (Z_0 - X_L t)(X_L + Z_0 t)} {Z_0 \left[ R_L^2+(X_L + Z_0 t)^2 \right]} [/math]
Now we choose the T-Line segment length d such that Gin = Y0 = 1 / Z0. This results in a quadratic equation for t:
[math] Z_0(R_L - Z_0)t^2 -2X_LZ_0 t + (R_L Z_0 -R_L^2 -X_L^2) = 0 [/math]
which can be solved for t. In the special case RL = Z0, there is one solution t = -XL / 2Z0. Otherwise, two distinct roots for t are found. Once t is found, the segment length can be calculated by solving t = tan (2π d / λg).
The stub susceptance B is chosen such that B = -Bin. From this condition, you can find the length of the stub depending on whether you use a short or open stub. Using the expressions for the impedance of an open-ended or shorted transmission line segment of length L given earlier in this tutorial, the equations for the length Ls of the open stub or short stub are found as:
[math] B_{open} = Y_0 tan (2\pi L_s / \lambda_g) = -B_{in} [/math]
[math] B_{short} = -Y_0 cot (2\pi L_s / \lambda_g) = -B_{in} [/math]
Double-Stub Impedance Matching Using Two Open Stubs
Additional parts you need for this part of the tutorial lesson:
- A Generic T-Line (Keyboard Shortcut: T)
- Two Generic Open Stubs
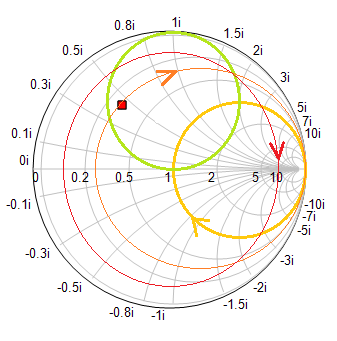
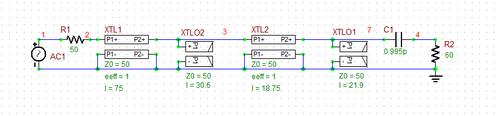
In the last part of this tutorial lesson, you will explore a double-stub matching network. The following figure on the left shows the original transmission line circuit of RF Tutorial Lesson 2 with a capacitive loading. The double-stub matching network will be inserted between the source circuit and the capacitive load of 60 - j80 Ohms at f = 2GHz. The figure on the right shows a shunt open stub connected in parallel with the load and a second shunt open stub placed at a distance of λg/8 = 18.75mm from the first stub towards the source through a segment of a 50Ω T-Line. When the lengths of the first and second open stubs are chosen to be 21.9mm and 30.6mm, respectively, the input impedance looking into the combination of the two stubs and the load to the right becomes 50Ω.
|
|
 |
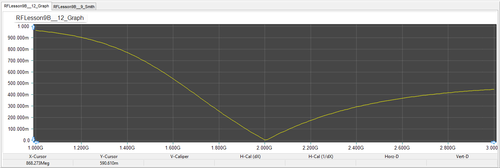
Similar to the previous case, run a network analysis of the circuit with the tuning stub matching network. Use Node 2 again as the input port. Plot the s11 data on the Smith chart with a frequency step size of 100MHz and then plot the return loss (|s11|) on a Cartesian graph with a frequency step size of 10MHz. As you can see from the results shown in the figures below, this network has a high return loss over most of the frequency range except around f = 2GHz and a prefect match is achieved at 2GHz.
 |
 |
A Summary of Double Stub Matching Theory
In this part of the tutorial we scrutinize the design procedure used in the previous part. The first shunt stub is connected in parallel with the load at the load location. Therefore, the total effective load at this point is:
[math]Y_{T} = G_L + j( B_L + B_1) [/math]
where YL = 1 / ZL = GL + j BL is the load admittance and B1 is the susceptance of the first shunt stub. After transforming this admittance through a T-Line segment of length d, the admittance just to the right of the second stub is given by:
[math]Y_{in} = G_{in} + j B_{in} = Y_0 \frac{ G_L + j\left(B_L + B_1 + Y_0 t \right) }{Y_0 + j \left( G_L + j B_L + j B_1 \right) t}[/math]
At this point, to achieve a perfect impedance matching, Gin must equal Y0 and Bin must equal -B2, where B2 is the susceptance of the second shunt stub. This leads to the following equation:
[math] G_L^2 -G_L Y_0 \frac{1+t^2}{t^2} + \frac{ \left( Y_0 -B_L t -B_1 t \right) ^2 } {t^2} = 0 [/math]
Remember that in double stub matching, we fix the distance d between the two shunt stubs. This length is usually chosen to be d = λg/8. In this case, t = tan(β d) = tan(2π d/λg) = tan(π/4) = 1. In this case, the above equation reduces to:
[math] G_L^2 - 2G_L Y_0 + \left( Y_0 -B_L -B_1 \right) ^2 = 0 [/math]
Solving the above equation, you can find B1 and the length of the first stub. From the equation B2 = -Bin, you can determine the length of the second stub. The two stubs can be open, short or mixed.
