| Tutorial Project: Network Analysis of a Simple Transmission Line Circuit & the Smith Chart
|
|
|
Objective: In this project, you will perform network analysis of simple transmission line circuits using the Smith chart.
|
|
Concepts/Features:
- Transmission Line
- Generic T-Line
- Network Analysis
- Multiport Network
- Scattering Parameters
- Impedance Parameters
- Smith Chart
|
|
Minimum Version Required: All versions
|
|
' Download Link: RF Lesson 3 Download Link: RF Lesson 3
|
What You Will Learn
In this tutorial you will run a network analysis test of the simple transmission line circuit you built in the previous tutorial lessons. You will examine the Z- and S-parameters of your circuit and study the Smith chart.
Building the RF Circuit
Once again you will use the simple transmission line circuit of RF Tutorial Lesson 1 with the AC voltage source and the quarter-wave impedance transformer configuration. The following is a list of parts needed for this part of the tutorial lesson:
|
|
| Part Name
|
Part Type
|
Part Value
|
| AC1
|
AC Voltage Source
|
1V
|
| XTL1
|
Generic T-Line
|
Defaults: Z0 = 70.71, eeff = 1, len = 37.5
|
| R1
|
Resistor
|
50
|
| R2
|
Resistor
|
100
|
Place and connect the parts as shown in the figure below:
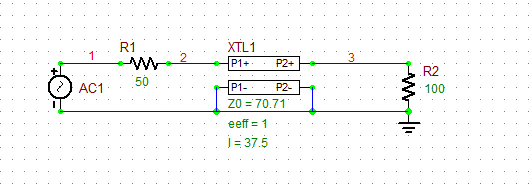 The quarter-wave impedance transformer circuit tuned for f 0 = 2GHz. |
Running a Network Analysis of Your RF Circuit
As a first step, you will run a "Network Analysis" test of your RF circuit. Network analysis calculates the S/Z/Y parameters of your circuit based on the port(s) you define for your RF circuit. In this case, you will define a one-port network with an input port established at the input of the T-Line between Node 2 and ground. In the Toolbox, select the Test Panel and check the "Network Analysis" checkbox. Open the Test's Settings dialog. It has three tabs at the top: Connections, Sweep and Output. In the first tab, Connections, you define the port(s) of your circuit. In this case, Port 1 is defined between Node 2 and the ground. Accept the default value of 50Ω for the "Reference Impedance". In the second tab, Sweep, set the start and stop frequencies to 1GHz and 5GHz, respectively. Select a linear scale interval and set the step size to 10MHz. This will provide a smooth graph of the port characteristics. In the third tab of the dialog, Output, go to the "Parameter Set" section and choose the S radio button to compute the scattering parameters. Since your circuit is a one-port, you will have the S11-parameter only. From the top "Graph Type" options, choose Cartesian (Mag/Phase). Check the checkboxes labeled Decibels and Degrees for magnitude and phase, respectively.
 The "Connections" tab of Network Analysis Test Panel. |
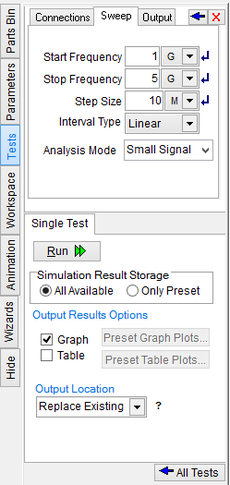 The "Sweep" tab of Network Analysis Test Panel. |
 The "Output" tab of Network Analysis Test Panel. |
Run a network analysis. An output graph like the one shown below is generated. This graph looks like a resonant circuit with a deep notch for |S11| at 2GHz. This is the frequency at which the input reflection coefficients becomes zero.
 Cartesian graph of the magnitude and phase of the S11-parameter. |
Next, go back to the Output tab of the Network Analysis Test Panel and choose the Z radio button in the "Parameter Set" section. Make sure you remove the check mark from the "Decibels" check box. From the top "Graph Type" options, choose Cartesian (Real/Imag), because you are more interested in the frequency response of the real and imaginary parts of the Z11-parameter, which are indeed the input impedance of your circuit.
 The "Connections" tab of Network Analysis Test Panel. |
Run another network analysis and view the output graph as shown below. Note that at 2GHz, the real part of the impedance is 50Ω and its imaginary part vanishes as you would expect for perfect impedance match.
 Cartesian graph of the real and imaginary parts of the Z11-parameter. |
Plotting the S-Parameter on Smith Chart
The Smith chart is a very useful graphical tool for RF engineers. RF.Spice A/D allows you to plot the S-parameters of your circuit on the Smith Chart. For this purpose, open the Network Analysis Test Panel of the Toolbox once again, and this time choose the S radio button in the "Parameter Set" section of the Output tab. For the "Graph Type", check the "Smith" checkbox. In order to better view the data points on the Smith chart, change the step size to 500MHz in the Sweep tab of the test panel. Run a network analysis of your RF circuit with the following parameters:
|
|
| Start Frequency
|
1G
|
| Stop Frequency
|
5G
|
| Steps/Interval
|
250Meg
|
| Interval Type
|
Linear
|
| Parameter Set
|
S
|
| Graph Type
|
Smith
|
At the end of the simulation, view the resulting Smith chart. Sometime, the program tries to fit the graph to the size of the graph window. If your graph window is elongated, the Smith chart will look elliptical. To make it circular, click on the graph window's title tab to make it active. Then open the Edit Graph tab of the Toolbox and press the Circle button/tab at the top of the panel. Then check box labeled Plot Circular Chart (Not Elliptical).
 |
The Smith chart is available for the S-parameter set only.
|
 The S11-parameter plotted on a Smith Chart. The tracking bar shows the points corresponding to 2GHz. |
Let's analyze the S11-parameter data plotted on the Smith chart in a little bit more detail. The S11-parameter data points over the frequency range 1-5GHz form a perfect circle around the center of the circular chart. The distance from the center is the magnitude of the reflection coefficient S11 (also known as the return loss). Since your T-Line segment is lossless (alpha = 0), its delivers the input signal to the load without attenuation. However, it causes a phase shift in the signal, which can also be interpreted as a time delay.
You can read the values of the data points on the Smith chart using the "Tracking Crosshairs" feature. For this purpose, click the Track Selected Plot  button of the Graph Toolbar and then move the mouse onto the surface of the Smith Chart. A tracking bar appears on the graph that connects the current cursor position to the data points. On the Status Bar, you can view the frequency associated with each data point as well as the real and imaginary parts of the reflection coefficient at that point. The 2GHz point is located at the center of the Smith chart.
button of the Graph Toolbar and then move the mouse onto the surface of the Smith Chart. A tracking bar appears on the graph that connects the current cursor position to the data points. On the Status Bar, you can view the frequency associated with each data point as well as the real and imaginary parts of the reflection coefficient at that point. The 2GHz point is located at the center of the Smith chart.
Exploring the Effect of Varying the Line Segment Length
From the transmission line theory, the input impedance of your basic transmission live circuit can be expressed as:
[math]Z_{in} = Z_0 \frac{Z_L + jZ_0 tan \beta L}{Z_0 + jZ_L tan \beta L}[/math]
and its input reflection coefficient is given by:
[math]\Gamma_{in} = \Gamma_L e^{-2j \beta L} = \frac{\zeta_L - 1} {\zeta_L + 1} e^{-2j \beta L} [/math]
where ΓL is the load reflection coefficient, ζL = ZL/Z0 is the normalized load value, L is the length of the line segment (same as the len parameter), and β = 2π/λg = 2π√(εeff)/λ0. Note that both input impedance and input reflection coefficient are functions of the product βL or the product 2π√(εeff)(f.L)/c, where c is the speed of light. For a given fixed value of εeff (same as the eeff parameter), both Zin and Γin are functions of the product (fL) rather than functions of f or L individually. This property has a practical application. If you fix the length of the transmission line segment and vary the frequency, you will get a circular plot on the Smith chart that is equivalent to changing the line segment length at a fixed frequency. For example, in the Smith chart of the previous step, L = 37.5mm was fixed. S11 at 2GHz falls at the origin of the Smith chart.
Now let's interpret the same circular curve at a fixed frequency of f = 2GHz, assuming that L now varies instead. The origin of the Smith chart obviously corresponds to L = 37.5mm. The point that corresponded to a frequency of 1GHz in the above Smith chart now would represent a line length of (1GHz × 37.5mm)/2GHz = 18.75mm. Similarly, the point that used to correspond to a frequency of 4GHz now would represent a line length of (4GHz × 37.5mm)/2GHz = 75mm.
|
|
| Point No.
|
Frequency @ L = 37.5mm
|
Length @ f = 2GHz
|
| 1
|
1GHz
|
18.75mm
|
| 5
|
2GHz
|
37.5mm
|
| 9
|
3GHz
|
56.25mm
|
| 13
|
4GHz
|
75mm
|
| 17
|
5GHz
|
93.75mm
|
The two Smith charts below show the one-to-one correspondence between the frequency points at a fixed length of 37.5mm and the length points at a fixed frequency of 2GHz.
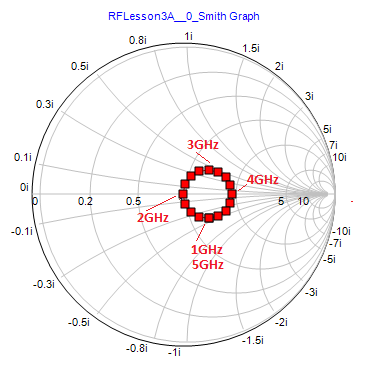 Smith chart showing the variation of the S11-parameter with frequency at a fixed line length of 37.5mm. |
 Smith chart showing the variation of the S11-parameter with line length at a fixed frequency of 2GHz. |
Investigating the Effect of an Inductive Load
As a next step, you will add an inductive component to your resistive load. Make sure that the length of the T-Line segment is the original 75mm value. Add a new inductor of value L = 6.37nH between the resistive load and the output of the T-Line segment.
 The quarter-wave impedance transformer circuit with an inductive load. |
At 2GHz, your termination load now has an impedance ZL = 100 + j80 Ohms. Run a new network analysis of your circuit with the parameters specified below:
|
|
| Start Frequency
|
1G
|
| Stop Frequency
|
5G
|
| Steps/Interval
|
250Meg
|
| Interval Type
|
Linear
|
| Parameter Set
|
S
|
| Graph Type
|
Smith
|
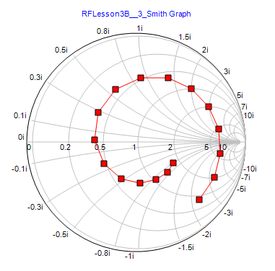
The figure below shows the S11-parameter data for the modified inductive load plotted on the Smith chart. Note that the curve is no longer a circle and has the shape of an expanding spiral. The inner and outer ends of the spiral correspond to the frequencies 1GHz and 5GHz, respectively.
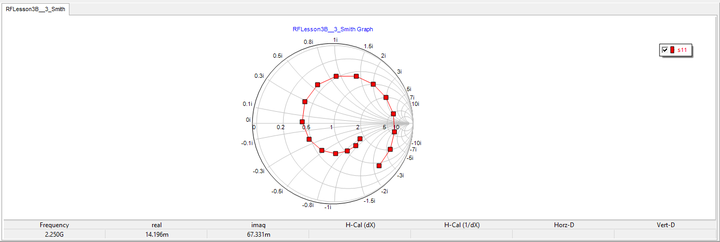 Computed s11 data for line segment length L = 75mm and Z L = 100 + j80 Ω over the frequency range 1-5GHz. |
 Back to RF.Spice A/D Tutorial Gateway
Back to RF.Spice A/D Tutorial Gateway












