RF Tutorial Lesson 2: Transient Analysis of a Simple Transmission Line Circuit
Contents
What You Will Learn
In this tutorial you will explore the transient response of transmission line circuits with various load configurations. You will also perform a Fourier analysis of non-sinusoidal signals.
Putting the Circuit Together
You will use the simple transmission line circuit of RF Tutorial Lesson 1 to start this project. However, instead of an AC voltage source, you will use a regular voltage source. The following is a list of parts needed for this part of the tutorial lesson:
| Part Name | Part Type | Part Value |
|---|---|---|
| VS | Voltage Source | Waveform: TBD |
| XTL1 | Generic T-Line | Defaults: Z0 = 50, eeff = 1, len = 10 |
| RS | Resistor | 50 |
| RL | Resistor | 50 |
| SOURCE | Voltage Probe Marker | N/A |
| IN | Voltage Probe Marker | N/A |
| OUT | Voltage Probe Marker | N/A |
Set the length of the T-Line segment to 60mm. Set the waveform of the voltage source to "Sinusoidal" with a frequency of 2GHz and a peak amplitude of 1V. The free-space wavelength at this frequency is λ0 = 150mm. Therefore, the length of your T-Line segment is 0.4λ0. Place three voltage probe markers (keyboard shortcut: Alt+L) called "SOURCE", "IN" and "OUT" as shown in the figure.
Transient Simulation of a Simple Transmission Line Circuit
Run a Transient Test of your circuit with the specified parameters below. Note that your Plot Edit List must already contain v(SOURCE), v(IN) and v(OUT). The node voltages of all voltage probe markers are automatically added to the Plot Edit List.
| Start Time | 0 |
|---|---|
| Stop Time | 3n |
| Linearize Step | 1p |
| Step Ceiling | 1p |
| Preset Graph Plots | v(source), v(in), v(out) |
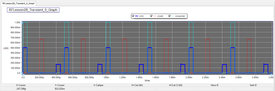
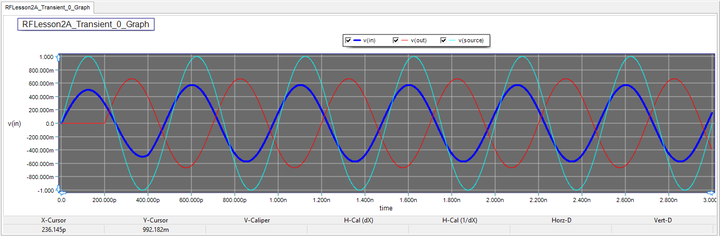
Run the simulation and observe the time-domain voltages. The period of your sinusoidal waveform is T = 1/f0 = 1 / 2GHz = 500ps. As you would expect, the T-Line segment is matched to both the source and the load. There are no reflections off either the input or the output of the transmission line. You can see that the output voltage has a delay of 200ps with respect to the input voltage, which is consistent with the calculation given below:
[math]\tau = \frac{L}{c} = \frac{60 mm}{3\times 10^8 m/s} = 200ps [/math]
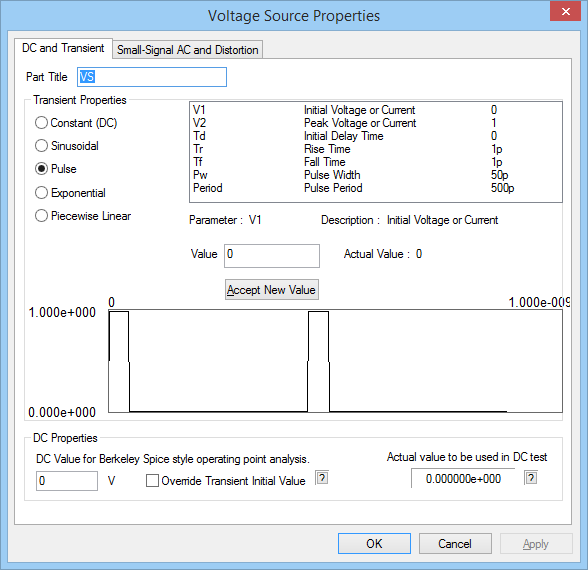
Next, you will try out a rectangular pulse waveform as your voltage source. Open the property dialog of VS and change the waveform type to "Pulse". Set the waveform parameters as specified below:
| Initial Voltage | 0 |
|---|---|
| Peak Voltage | 1 |
| Delay Time | 0 |
| Rise Time | 1p |
| Fall Time | 1p |
| Pulse Width | 50p |
| Pulse Period | 500p |
The duty cycle of the pulse train waveform is therefore 10%. Run a new transient test of your circuit with the same test parameters as before and compare the results to the previous case of a sinusoidal waveform. Here, too, there is a 200ps delay between the input and output voltages. Due to the perfect impedance match at both the input and output, v(in) and v(out) have equal amplitudes of 0.5V. Moreover, v(in) is simply is half-scaled replica of the source voltage.
Investigating the Effect of Load Mismatch
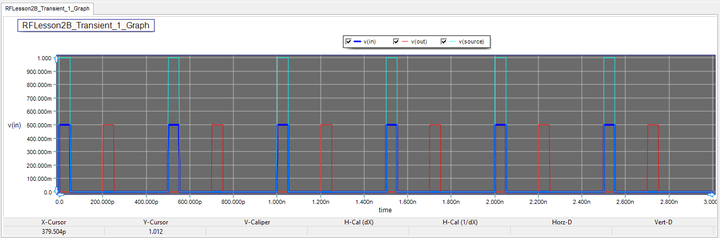
Now change the load resistor to RL = 100Ω. Run the Transient Test with the same settings as before for both cases of sinusoidal and pulse waveforms:
| Start Time | 0 |
|---|---|
| Stop Time | 3n |
| Linearize Step | 1p |
| Step Ceiling | 1p |
| Preset Graph Plots | v(source), v(in), v(out) |
The results of the two cases are shown in the figures below:
As you can see from these figures, the effect of the load mismatch in the sinusoidal signal case is the difference in the amplitudes of the input voltage and load voltage. This is due to the nonzero load reflection coefficient:
[math] \Gamma_L = \frac{ Z_L - Z_0 }{ Z_L + Z_0 } = \frac{ 100 - 50 }{ 100 + 50 } = \frac{1}{3} [/math]
In the case of the pulse waveform, the impedance mismatch introduces a reflected pulse that reaches node "IN" after a delay of 400ps, which is the round-trip time from the input point to the load and back. The amplitude of the smaller reflected pulse (166.7mv) is 1/3 the amplitude of the larger incident pulse (500mV) as you would expect from the value of the reflection coefficient.
Analyzing a Quarter-Wave Impedance Transformer
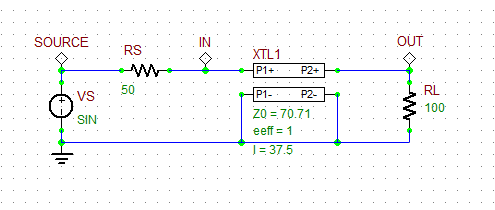
In RF Tutorial lesson 1, you designed a quarter-wave impedance transform to match an arbitrary resistive load to a 50Ω source. Set the length of the T-Line segment to L = λ0/4 = 37.5mm for an operating frequency of 2GHz. Also, set the characteristic impedance of the T-line to Z0 = √(100.50) = 70.71Ω. Run a new transient test with the same settings as before for both cases of sinusoidal and pulse waveforms:
| Start Time | 0 |
|---|---|
| Stop Time | 3n |
| Linearize Step | 1p |
| Step Ceiling | 1p |
| Preset Graph Plots | v(source), v(in), v(out) |
The results are shown and compared in the figures below:
The input impedance of the quarter-wave T-Line segment (at 2GHz) is given by:
[math] Z_{in} = \frac{Z_{0c}^2}{Z_L} = \frac{70.71^2}{100} = 50\Omega [/math]
As you can see from the above figure, in the case of the "pure harmonic" sinusoidal excitation, the source voltage is equally split between the source resistor RS and the input port of the T-Line. However, the situation is slightly different in the case of pulse waveform. The dispersive effects of the transmission line are in full display in this case. In other words, the matching condition is satisfied only at 2GHz and not at its harmonics present in the pulse waveform. Note that both load and source reflection coefficients are nonzero for this circuit:
[math] \Gamma_L = \frac{ Z_L - Z_{0c} }{ Z_L + Z_{0c} } = \frac{ 100 - 70.71 }{ 100 + 70.71 } = 0.172 [/math]
[math] \Gamma_S = \frac{ Z_S - Z_{0c} }{ Z_S + Z_{0c} } = \frac{ 50 - 70.71 }{ 50 + 70.71 } = -0.172 [/math]
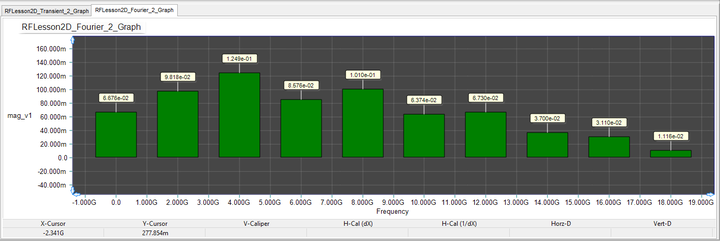
To better understand this point, you can use RF.Spice's Fourier analysis feature, which is part of the transient test. You will run the "Transient Test" for the pulse waveform two more times with the "Fourier Analysis" enabled in the Transient Test Panel. Check the "Apply Fourier" checkbox and click the "Fourier Setup" button to open the Fourier Transform Settings dialog. Set the Fundamental Frequency to 2GHz and set the reference output node to "0" for the ground. Then, set the positive output node to "1" for the source voltage in the first run and then to "2" for the input voltage in the second run. At the end of the simulation, additional bar chart graphs are added to the Data Manager window. The spectral contents of the source and input voltages are shown in the figures below. You can clearly see that both signals have significant DC contents as well as sizable higher harmonics.
Investigating the Effect of a Capacitive Load
In the last part of this tutorial lesson, you add a 0.1pF shunt capacitor called "CL" to the load and see its effect in the case of pulse train signal. The modified circuit is shown in the opposite figure. The impedance of the shunt capacitor at the nth harmonic of the source's 2GHz fundamental frequency is given by:
[math] Z_{Cap} = -\frac{j}{\omega C_L} = -\frac{j}{2\pi n (2\times 10^9)(0.1\times 10^{-12})} \approx -j(796/n) \ \Omega [/math]
It can be seen that at the fundamental frequency, the capacitor has very negligible effect, but at higher harmonics, its impedance becomes comparable to the 100Ω resistive loads.
Run a transient test of your modified circuit with the same settings as before only for the case of pulse waveform:
| Start Time | 0 |
|---|---|
| Stop Time | 3n |
| Linearize Step | 1p |
| Step Ceiling | 1p |
| Preset Graph Plots | v(source), v(in), v(out) |
Enable the "Fourier Analysis" for Node 2 with a fundamental frequency of 2GHz. The figures below show the simulation results. You can see from the top figure that the output voltage has been slightly deformed with a rounded rising edge. Also, the reflected pulse now has significant undershoot and overshoot at its rising and falling edges, respectively. Next, compare the spectral contents of v(in) for the two cases without and with the shunt capacitor. The contents at DC, fundamental frequency and first few harmonics are almost the same, but the results start to differ at higher harmonics as we justified earlier.