RF Tutorial Lesson 1: AC Analysis of a Simple Transmission Line Circuit
Contents
What You Will Learn
In this tutorial you will build a simple RF circuit consisting of a generic transmission line segment, whose input is connected to an AC voltage source with an internal resistance and whose output is connected to a terminating load. The purpose of this tutorial is to help you become familiar with AC Frequency Sweep analysis of RF circuits. It is assumed that by this time you have already completed the first few analog tutorial lessons and are comfortable with navigating the RF.Spice A/D Workshop.
Placing the Parts
To build your first RF circuit, you need the following parts:
| Part Name | Part Type | Part Value |
|---|---|---|
| AC1 | AC Voltage Source | 1 |
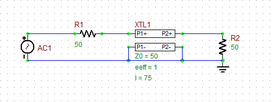
| XTL1 | Generic T-Line | Defaults: Z0 = 50, eeff = 1, len = 10 |
| R1 | Resistor | 50 |
| R2 | Resistor | 50 |
Create and place the above parts on the Schematic Editor. Keep in mind that you can create and place these parts either using keyboard shortcuts, or from the "RF Menu" of RF.Spice A/D or from the "Parts Bin" tab of the Toolbox on the left side panel. The keyboard shortcut for the AC Voltage Source is Alt+V and the keyboard shortcut for the T-Line is T. Note that instead of an "AC Voltage Source", you may also choose to place a regular voltage source and check its AC "Use" checkbox in its property dialog just like in all other AC circuits of RF.Spice A/D. Both methods create the same type of AC source.
Connect the part as shown in the figure below. It is very important to ground both the input and output negative pins of the Generic T-Line device (i.e. P1- and P2-).
Next, open up the property dialog of the T-Line part by double-clicking on its symbol in the Schematic Editor. You will see a list of the device's parameters. You will keep the default characteristic impedance value of Z0 = 50Ω, the default effective permittivity value of eeff = 1.0, and the default zero attenuation constant. Change the length of the line segment to 75mm. To do so, select the "len" row in the parameter list, and type in the value 75 to replace the default 10, and click the "Accept Value" button of the dialog.
Running an AC Sweep Analysis of Your RF Circuit
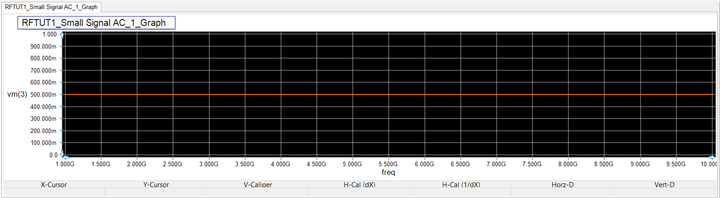
At this time your RF circuit consists of a 50Ω transmission line segment that is matched at its input to the 1V voltage source with an internal resistance of 50 Ohms and is also matched at its output to a resistive 50Ω termination load. Therefore, you do not expect any mismatch and signal reflection at either of the two ports of the T-Line. Due to the perfect impedance match, the source voltage is equally divided between its internal resistance and the input to the T-Line, i.e. 0.5V. On the other hand, since the T-Line is lossless, the input 0.5V voltage is transferred unchanged to the 50Ω output load.
Run an AC Frequency Sweep test of your circuit from the Test Panel. Set the start and stop frequencies to 1GHz and 10GHz, respectively. Choose a "Linear" interval and set the step size to 10MHz. Click the "Preset Graph Plots" button of the test panel to open the Edit Plot List dialog. In the complex signal settings section, choose the "Magnitude/Phase (Degrees)" format and then select the node voltage magnitudes V(2) and V(3) at the input and output ports of the T-Line. Run the AC test. The output graph will show two overlapping constant voltages over the entire 1-10 GHz frequency range as expected.
The program usually plots the graphs with reasonable axis scales and other suitable plot settings. Oftentimes, you may want to change the default graph settings. For example, in the case of the V(2) and V(3) plots, they are identical and constant, i.e. they have the same minimum and maximum left axis limits. To better view this graph, while the graph window is active, click the Edit Axes tab of the Toolbox. From the top Axis drop-down list, select the "Left Axis". Remove the check mark from the "Auto" checkbox and enter values 0 and 1 in the Min and Max boxes, respectively. Make sure to click the button labeled "Apply Above Changes". Also, the AC sweep results are usually plotted on a horizontal axis (X-Axis) with a logarithmic scale. In the same Edit Axes tab, select the "Bottom Axis" from the Axis drop-down list and remove the check mark from "Logarithmic" checkbox.
Investigating the Effect of Load Mismatch
Now change the value of the load resistor 1 Ohm, 25 Ohms, 100 Ohms and finally to 100k Ohms and run the AC sweep test for each load value according to the table below.
| Start Frequency | 1G |
|---|---|
| Stop Frequency | 10G |
| Steps/Interval | 10Meg |
| Interval Type | Linear |
| Preset Graph Plots | vm(2), vm(3) |
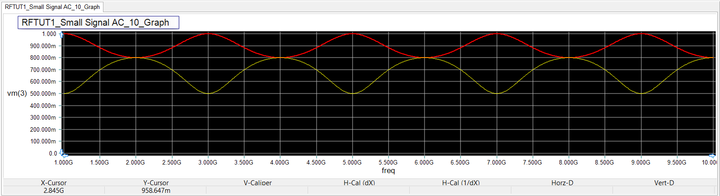
The figures below show the frequency response of your RF circuit, in which the yellow signal represents V(2) and the red signal represents V(3). As you can see from the these figures, the input voltage V(2) oscillates as a function of frequency, while the output voltage V(3) is still constant over the entire frequency range. The latter is due to the fact that looking from the output of the T-Line to the left, you see an impedance-matched circuit, and this condition does not change as a function of frequency.
Note that the extreme load values R2 = 1Ω and R2 = 100kΩ approximate the case of open end and short circuits, respectively. For this values, the these limit values, the input voltage fluctuate between 0 and 1V. Keep in mind that RF.Spice A/D provides special generic Open Stub and Short Stub devices that can be used for this purpose. You will use open and short stub parts later in Tutorial Lesson 3 for impedance matching.
To explain these figures, recall from the basic transmission line theory that the voltage at any point on a transmission line segment is given by:
[math]V(z) = V_0^+ \left[ e^{-j\beta z} + \Gamma_{L} e^{+j\beta z} \right] [/math]
where the load reflection coefficient ΓL is given by:
[math]\Gamma_{L} = \frac{Z_L - Z_0}{Z_{L} + Z_0}[/math]
ZL is the complex load impedance, V0+ is a contant, and the coordinate z = 0 is assumed to be the location of the load. Thus, the two voltages V2 and V3 are given by:
[math]V_2 = V(z = -L) = V_0^+ \left[ e^{j\beta L} + \Gamma_{L} e^{-j\beta L} \right] [/math]
[math]V_3 = V(z = 0) = V_0^+ \left[ 1 + \Gamma_{L} \right] [/math]
Therefore, one can write
[math] \frac{V_3}{V_2} = \left( \frac { 1 + \Gamma_{L} e^{-2j\beta L} } {1 + \Gamma_{L}} \right) e^{j\beta L} [/math]
From the above equations, you can see that V3 = V(z = 0) is a constant and therefore independent of frequency. On the other hand, V2 = V(z = -L) is a function of βL. Since βL = 2π(L/λg) = 2πf√εeff /c, V2 is therefore a function of frequency as you can see from its variation in the above figures.
With Z0 = 50Ω, the following table shows the values of the load reflection coefficient for different load values:
| ZL | ΓL |
|---|---|
| 0 | -1.0000 |
| 1Ω | -0.9608 |
| 25Ω | -0.3333 |
| 50Ω | 0 |
| 100Ω | 0.3333 |
| 100kΩ | 0.9990 |
| ∞ | 1.0000 |
Investigating the Effect of Source Mismatch
Next, fix the load value at R2 = 100Ω and change the value of the source resistance to R1 = 25Ω. Run the AC Sweep test once more according to the table below:
| Start Frequency | 1G |
|---|---|
| Stop Frequency | 10G |
| Steps/Interval | 10Meg |
| Interval Type | Linear |
| Preset Graph Plots | vm(2), vm(3) |
As you can see from the output graphs, this time both the input voltage V(2) and output voltage V(3) fluctuate as a function of frequency, as you have both load mismatch and source mismatch.
Designing a Quarter-Wave Impedance Transformer
Quarter-wave impedance transformer are often used for impedance matching between two transmission lines of different characteristic impedances Zo1 and Zo2. In that case, a line segment of length L = 0.25λg with a characteristic impedance of Z0 = √( Zo1 . Zo2 ) is inserted between the two transmission lines. In this part of the tutorial lesson, we design a quarter-wave impedance transformer that matches your 100Ω resistive load to the voltage source with the 50Ω internal resistance.
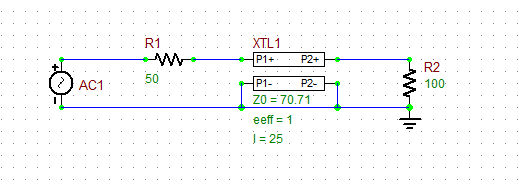
Quarter-wave impedance transformers are narrowband devices because they are designed based on a certain length at a specific frequency. You will design your quarter-wave impedance transformer to operate at 3GHz. At this frequency, the free-space wavelength is λ0 = 3×108 / 3×109 = 0.1m = 100mm. Since your Generic T-Line is of the TEM-type (eeff = 1), therefore, λg = λ0 = 100mm. Also, Z0 = √(100 . 50) = 70.71Ω. So you need a 25mm, 70.71Ω T-Line segment. Open the property dialog of your T-Line part and change its characteristic impedance to Z0 = 70.71 and its length to len = 25mm. Keep the default values of the other parameters: eeff = 1 and alpha = 0. Run a new AC Sweep test again as specified below:
| Start Frequency | 1G |
|---|---|
| Stop Frequency | 10G |
| Steps/Interval | 10Meg |
| Interval Type | Linear |
| Preset Graph Plots | vm(2), vm(3) |
This time, the source will see a matched transmission line between Node 2 and the ground at the frequency f = 3GHz. In other words, the input impedance of the T-Line looking to the right at Node 2 is 50 Ohms at 3GHz. The source voltage is equally divided between the source impedance and the input of the T-Line. Therefore, V(2) = 0.5V at 3GHz as can be seen from the figure below. Also, since the generic T-Line is a reciprocal device, the load at the other end of the T-line is impedance-matched at f = 3GHz, too. In other words, the input impedance of the T-Line looking to the left at Node 3 from the point of view of the resistive load is 100 Ohms at 3GHz. As you can see from the figure, this results is much more subdued oscillations of the load voltage over the entire frequency band.