EM.Ferma Tutorial Lesson 1: Computing The Electric Field & Potential Due To Spherical Charges
Contents
- 1 What You Will Learn
- 2 Getting Started
- 3 Creating a Charge Source Group
- 4 Drawing a Spherical Object
- 5 Examining the Mesh of the Physical Structure
- 6 Defining the Simulation Observables for Your Project
- 7 Running the Electrostatic Simulation
- 8 Visualizing the Simulation Data
- 9 Verifying Your Simulation Results
- 10 Adding a Second Identical Spherical Charge
- 11 Simulating Two Opposite Spherical Charges
What You Will Learn
This tutorial will guide you through all the necessary steps required to set up and perform a basic electrostatic simulation and visualize and graph the simulation results. Specifically, you will draw spherical charge objects and analyze their electric field and potential.
| |
We strongly recommend that you read through the first few tutorials and study them carefully before setting up your own projects. |
![]() Back to EM.Ferma Tutorial Gateway
Back to EM.Ferma Tutorial Gateway
![]() Download projects related to this tutorial lesson
Download projects related to this tutorial lesson
Getting Started
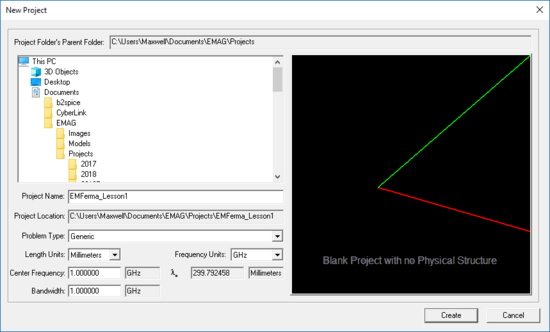
Open the EM.Cube application by double-clicking on its icon on your desktop. By default, EM.Cube opens a blank project with the name “UntitledProj0” in its CubeCAD Module. You can start drawing objects and build up your physical structure right away. Or you can initiate a new project by selecting the New ![]() button of the System Toolbar or using the keyboard shortcut Ctrl+N. This opens up the New Project Dialog, where you can enter a title for your new project and set its path on your hard drive. From the same dialog, you can also set the project’s length units, frequency units, center frequency and bandwidth.
button of the System Toolbar or using the keyboard shortcut Ctrl+N. This opens up the New Project Dialog, where you can enter a title for your new project and set its path on your hard drive. From the same dialog, you can also set the project’s length units, frequency units, center frequency and bandwidth.
For this tutorial lesson, set the following parameters in the new project dialog:
Click the Create button of the dialog to accept the settings. A new project folder with your given name is immediately created at your specified path.
To navigate to EM.Ferma, simply select its icon from the Module Toolbar on the left side of the screen. Selecting the module icon changes the contents of the navigation tree to reflect the types of objects supported by the current module.
| |
EM.Ferma is a static simulator that solves electromagnetic problems at DC or under low-frequency quasi-static approximation. Therefore, always leave the project's center frequency and bandwidth at their default value of 1GHz, as they are not used by the static simulations. |
Creating a Charge Source Group
Before you draw a spherical charge object, you have to create a charge object category on the navigation tree. In EM.Ferma, objects are grouped together and organized by their static behavior under the “Physical Structure” node of the navigation tree. There are several categories to choose from: fixed-potential PEC objects, dielectric/magnetic materials, volume charges, etc. All the objects belonging to the same charge group have the same color and the same charge density.
To create a new charge category, right-click on the Volume Charges (Heat Sources) item in the navigation tree and select Insert New Charge Source... from the contextual menu. The New Charge Source dialog opens up with a default name CS_1 and a default purple color. In the section titled "Source Properties", you will see a default value of -1e-5C/m3 for Charge/Heat Density. This means a default negative charge. Replace this with a positive value of +1e-8 C/m3. Click the OK button and close the dialog and return to the project workspace (main window). The last object group created in the navigation tree remains as the "Active" group, and its name is displayed in bold letters, meaning that all the objects you draw will belong to this group.
Drawing a Spherical Object
Select the Sphere Tool ![]() button of the Object Toolbar or select the menu item Object → Solid → Sphere.
button of the Object Toolbar or select the menu item Object → Solid → Sphere.
With the sphere tool selected, click at the origin (0,0,0) of the project workspace to start your drawing, and drag the mouse to draw a sphere of radius R = 5mm. A property dialog pops up at the lower right corner of the screen. You can see the radius of the new sphere changing in this dialog as you drag your mouse. When the radius reaches a value of 5 units, left-click to lock-in the value. You may also left-click at any point and adjust the length by typing in a value of 5 in the object’s property dialog.
Once you draw your new object, its name "Sphere_1" is added to the navigation tree under CS_1 group, where it belongs. Note that a default blue box is automatically placed around the object. This is called the domain box. Since EM.Ferma's simulation engine uses a finite difference scheme to solve the Laplace or Poisson equations, it requires a finite-sized computational domain. The default domain box automatically adjusts itself to enclose the largest bounding box of the entire physical structure.
Once your drawing is complete, you can zoom to fit your structure into the screen using the keyboard shortcut Ctrl+E or by clicking the Zoom Extents ![]() button of View Toolbar. If you have a mouse with a scroll wheel, you can use the scroll wheel to zoom in or zoom out while you draw an object. You can also rotate the view using the right mouse button, or pan the view using the right mouse button while holding the keyboard’s Shift Key down.
button of View Toolbar. If you have a mouse with a scroll wheel, you can use the scroll wheel to zoom in or zoom out while you draw an object. You can also rotate the view using the right mouse button, or pan the view using the right mouse button while holding the keyboard’s Shift Key down.
Examining the Mesh of the Physical Structure
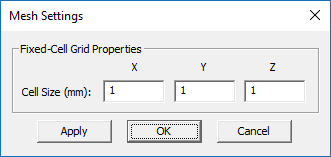
In order for EM.Ferma to solve the Laplace or Poisson equations using the finite difference method, the computational domain must be discretized into a large number of elementary cells. EM.Ferma uses a fixed-cell grid to discretize the computational domain. You can control the mesh cell size and therefore the total number of cells along the X-, Y- and Z-axes independently. The mesh properties can be accessed by clicking the Mesh Settings ![]() button of the Simulate Toolbar or using the keyboard shortcut Ctrl+G or selecting the menu item Simulate → Discretization → Mesh Settings. The default mesh cell size is 1 project unit along all three principal directions.
button of the Simulate Toolbar or using the keyboard shortcut Ctrl+G or selecting the menu item Simulate → Discretization → Mesh Settings. The default mesh cell size is 1 project unit along all three principal directions.
To view the mesh, click the Show/Generate Mesh ![]() button of the Simulate Toolbar or alternatively use the keyboard shortcut Ctrl+M. In general, the mesh view shows how the simulation engine sees your physical structure. You can also display the three mesh grid planes by right-clicking on one of the three items XY Grid Plane, YZ Grid Plane, or ZX Grid Plane in the “Discretization” section of the navigation tree and selecting Show from the contextual menu. To remove the grid planes from the project workspace, open the same contextual menu and select Hide. You can move the grid planes across the computational domain using PageUp or PageDown buttons.
button of the Simulate Toolbar or alternatively use the keyboard shortcut Ctrl+M. In general, the mesh view shows how the simulation engine sees your physical structure. You can also display the three mesh grid planes by right-clicking on one of the three items XY Grid Plane, YZ Grid Plane, or ZX Grid Plane in the “Discretization” section of the navigation tree and selecting Show from the contextual menu. To remove the grid planes from the project workspace, open the same contextual menu and select Hide. You can move the grid planes across the computational domain using PageUp or PageDown buttons.
For this tutorial project, open the mesh settings dialog and set the cell size along all the three directions X, Y and Z to 0.5mm to generate a finer mesh.
Use the Apply button of the mesh settings dialog to regenerate the mesh and see the effect of your new settings.
Defining the Simulation Observables for Your Project
Project observables are output quantities that you would like to compute at the end of an electrostatic simulation. Field sensors are used to visualize the near fields of your structure and the electric potential on a plane parallel to one of the three principal planes. The field sensor planes extend across the entire computational domain. To define a field sensor, right click on the Near-Field Sensors item in the “Observables” section of the navigation tree and select Insert New Observable… In the Field Sensor Dialog, enter the point (0, 0, 0) for Coordinates and select Z from the drop-down list labeled Direction. This means that your field sensor plane will be the XY plane, which passes through the center of the sphere. Accept the other default settings in the dialog box, and select OK to continue. A new item "Sensor_1" is added to the navigation tree, and the field sensor is now represented in the project workspace by a purple plane across the computational domain.
Running the Electrostatic Simulation
At this time, your project is ready for electrostatic simulation. Click the Run ![]() Button of the Simulate Toolbar to open up the Simulation Run Dialog. Or alternatively, use the keyboard shortcut Ctrl+R, or select the menu item Simulate → Run… The simplest simulation mode in EM.Ferma is “Analysis”. In this mode, your physical structure is taken “As Is”, and its mesh is passed to the electrostatic simulation engine along with the necessary information regarding the sources and observables.
Button of the Simulate Toolbar to open up the Simulation Run Dialog. Or alternatively, use the keyboard shortcut Ctrl+R, or select the menu item Simulate → Run… The simplest simulation mode in EM.Ferma is “Analysis”. In this mode, your physical structure is taken “As Is”, and its mesh is passed to the electrostatic simulation engine along with the necessary information regarding the sources and observables.
To run the simulation, click the Run button of the simulation run Dialog. A separate window pops up displaying messages from the simulation engine. Once the simulation has been completed, you can close the message window and return to the project workspace. The navigation tree is now populated with simulation results in its "Field Sensors"" section.
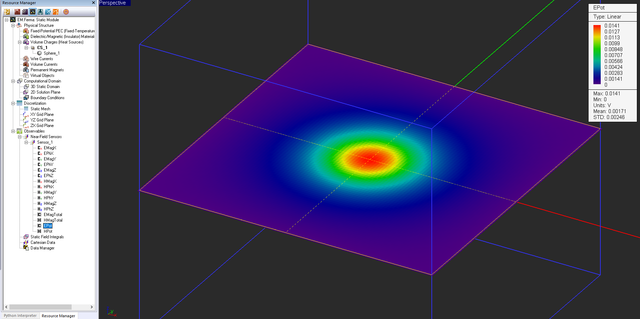
Visualizing the Simulation Data
EM.Cube’s computational modules usually generate two types of data: 2D and 3D. 2D data are graphed. 3D data are visualized in EM.Cube’s project workspace, and the plots are usually overlaid on the physical structure. The field sensor section of the navigation tree has a list of twelve amplitude and phase plots for all the six field components: Ex, Ey, Ez, and Hx, Hy, Hz. There are also two additional plots for the magnitude of total electric field and total magnetic field as well as the electric scalar potential and the magnitude of the magnetic vector potential. In an electrostatic simulation, the magnetic field is assumed to be zero. Therefore, you will only have electric field and electric potential plots. Moreover, both the field and potential are real-valued. The electric potential is plotted on a color-coded intensity plots that may involve both negative and positive values. Click on any of these plots to display them in the project workspace. You can use the standard view operations such as dynamic zoom, rotate view, pan view, etc. to better examine these plots.
Verifying Your Simulation Results
Consider a spherical charge of radius a and uniform charge density ρ0. Due to the symmetry of the spherical charge, you would expect the electric field to be radial and uniform at all spherical observation angles. In other words,
[math] \mathbf{E(r)} = E_r(r) \mathbf{\hat{r}} [/math]
Applying Gauss' law to a spherical surface of radius r, one can write:
[math] \int\int_{S_o} \epsilon_0 \mathbf{E(r)} . \mathbf{ds} = \int\int\int_{V} \rho (r) dv = Q_{tot} [/math]
or
[math] \epsilon_0 E_r(r) \left( 4\pi r^2 \right) = \rho_0 \left( \frac{4}{3} \pi R^3 \right) [/math]
where ε0 = 8.8542×10-12 F/m is the permittivity of the free space, and R = r if r ≤ a and R = a if r > a. Then, one can derive the following relationships for the electric field of a uniform spherical charge distribution:
[math] E_r(r) = \frac{\rho_0}{3\epsilon_0}r, \ \ \ \ \ \ \ r\le a [/math]
[math] E_r(r) = \frac{a^3\rho_0}{3\epsilon_0} \frac{1}{r^2} = \frac{1}{4\pi\epsilon_0} \frac{Q_0}{r^2}, \ \ \ \ \ r\gt a [/math]
where Q0 = Qtot = 4πa3ρ0/3. The last equation above is nothing but Coulomb's law. For the spherical charge object you built earlier, at r = 5mm, you will find:
[math] E_r(r = 0.005m) = \frac{(10^{-8})(5\times 10^{-3})}{3 \times 8.8542 \times 10^{-12}} = 1.882 V/m [/math]
Besides the color-coded electric field distribution maps, EM.Ferma also generates 2D Cartesian graphs of the total electric fields along the crosshairs of the field sensor plane. You can move the crosshairs around by changing the Coordinates values in the field sensor dialog. By default, the crosshairs of your field sensor plane are set at X = Y = 0.
A list of all the 2D output data files generated at the end of a simulation can be viewed in EM.Ferma’s Data Manager. To open this dialog, click the Data Manager ![]() button of Simulate Toolbar, or use the keyboard shortcut Ctrl+D, or access the menu item Simulate → Data Manager, or right-click on the Data Manager item in the “Observables” section of the navigation tree and select Open Data Manager…
button of Simulate Toolbar, or use the keyboard shortcut Ctrl+D, or access the menu item Simulate → Data Manager, or right-click on the Data Manager item in the “Observables” section of the navigation tree and select Open Data Manager…
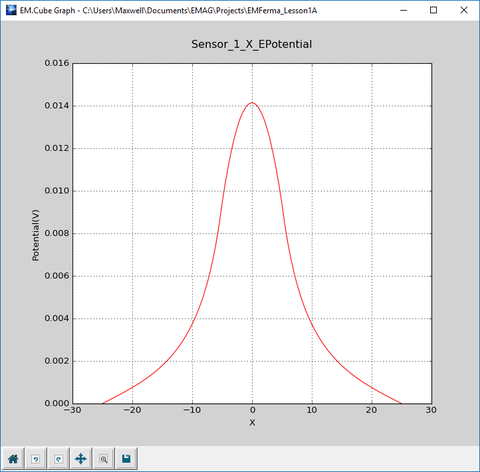
Select the data files “Sensor_1_X_ETotal.DAT” and "Sensor_1_X_EPotential.DAT" by highlighting them in the data manager's list. Note that you can make multiple selections using your keyboard's Ctrl or Shift keys. Click the Plot button of the dialog. A PyPlot graph window pops up that shows the the total E-field and the electric potential as functions of the coordinate X as shown in the figures below.
The graphs are interactive. As you move the mouse on the graph, you can read the value of the horizontal axis (X) and the corresponding value of the total electric field distribution along the Y direction on the lower right corner of the status bar. The PyPlot window has also a number of controls that let you change the settings of your graph using your mouse. For example, using the Pan/Zoom button ![]() , you can pan the graph with the left mouse button and zoom it in or out with the right mouse button. A combination of the two operations usually gives you an ideal scaling of your graph.
, you can pan the graph with the left mouse button and zoom it in or out with the right mouse button. A combination of the two operations usually gives you an ideal scaling of your graph.
From the figure below, you can see that the electric field increases linearly from r = 0 to r = 5mm, where it reaches a value of 1.9V/m as read by the tracking crosshairs. This is very close to the value we calculated earlier. The electric field then quickly drops down as 1/r2 in the free space.
Adding a Second Identical Spherical Charge
While the "CS_1" charge group is active in the navigation tree, you can draw new geometric objects in the workspace under the same group and all of those object will have the same purple color and the same positive charge density. You can also copy and paste objects. Select Sphere_1 by clicking on it. It color changes to bright yellow, which is the default selection color. Click the Copy ![]() button of the System Toolbar at the top of the project workspace or simply use the keyboard shortcut Ctrl+C. Next, click the Paste
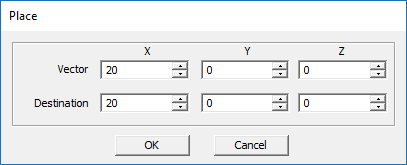
button of the System Toolbar at the top of the project workspace or simply use the keyboard shortcut Ctrl+C. Next, click the Paste ![]() button of the System Toolbar or simply use the keyboard shortcut Ctrl+V to place a copy of the selected object. When you paste a geometric object in EM.Cube, the "Place" dialog pops up at the lower right corner of the screen. This gives you a chance to move and place your copy at the desired location. You can either enter the X, Y , Z components of the translation vector or just enter the coordinates of the destination. In this case, enter the coordinates (20mm, 0, 0).
button of the System Toolbar or simply use the keyboard shortcut Ctrl+V to place a copy of the selected object. When you paste a geometric object in EM.Cube, the "Place" dialog pops up at the lower right corner of the screen. This gives you a chance to move and place your copy at the desired location. You can either enter the X, Y , Z components of the translation vector or just enter the coordinates of the destination. In this case, enter the coordinates (20mm, 0, 0).
A new purple sphere called "Sphere_2" appears in the project workspace and its name is added to the navigation tree under "CS_1". Note that the domain box automatically expands to enclose both sphere objects.
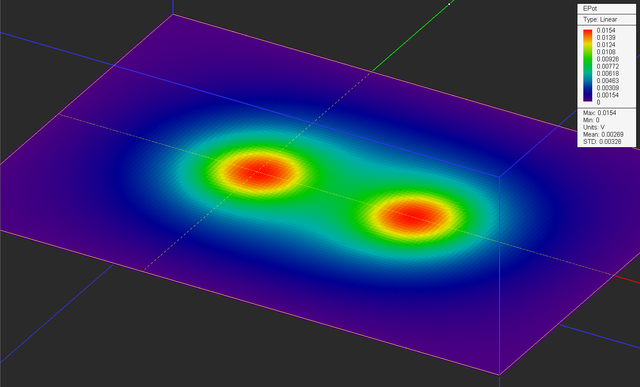
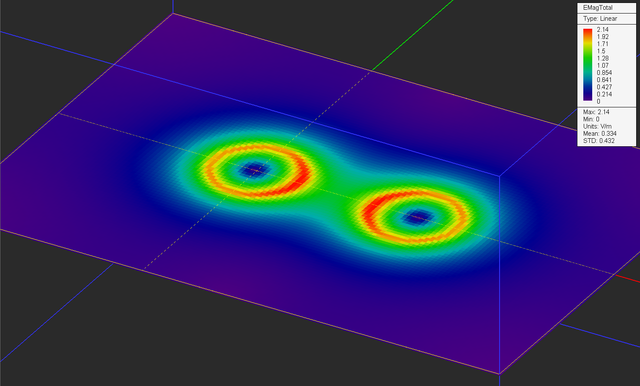
Run an electrostatic simulation of your new physical structure and visualize the total electric field and electric scalar potential maps as shown in the figures below.
The 3D field plots are displayed as intensity plots by default. You can also shows them as vector plots made up of a collection of arrows whose orientation, color and length indicate both the direction and strength of the field. To do so, right-click on the name of "Sensor_1" in the navigation tree and select Properties from the contextual menu. In the field sensor dialog, choose Vector as the Plot Type. Also, set the values of Max Size to 0.5mm and Cone Length Ratio and Cone Radius Ratio to 0.5 as shown below. You can freeze any geometric objects to see other objects hidden behind, beneath or inside it. In that case, you will see a wireframe outline of the frozen object and you cannot select it. To freeze an object, right-click on its surface in the project workspace or right-click on its name in the navigation tree and select Freeze from the contextual menu. To unfreeze, repeat the same procedure. Freeze Sphere_1 and Sphere_2 objects. Now visualize the total electric field map as shown in the figure below.
Simulating Two Opposite Spherical Charges
In the last part of this tutorial lesson, you will add a negative spherical charge to your physical structure. For this purpose, you need to define a new volume charge source group. Repeat the same procedure as in the beginning of this tutorial lesson and define a charge source group called "CS_2". Choose a hot pink color for it and set its charge density to -1e-8C/m3.
You can delete the positive charge "Sphere_2" you drew earlier and then draw a new sphere object of negative charge under the currently active group of the navigation tree, i.e. "CS_2". Or alternatively, you can move the object "Sphere_2" from the first group "CSC_1" to the new group "CS_2". To do the latter, right-click on the name of "Sphere_2" in the navigation tree and select Move To → EM.Ferma → CS_2 from the contextual menu. The color of the sphere turns into hot pink.
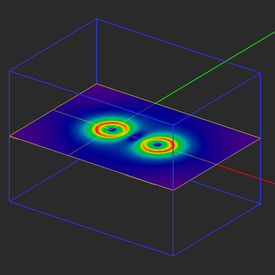
Run an electrostatic simulation of your new physical structure and visualize the total electric field and electric scalar potential maps as shown in the figures below. In the case of the electric potential map, note that color scale goes from a negative lower bound to a positive upper bound.
Also, visualize a vector plot of the total electric field distribution following the same procedure and using the same settings mentioned earlier.