Digital Tutorial Lesson 6: Building a Digital Ripple-Carry Adder
Building Your Own Reusable Binary Adder Digital Device
Objective
In this tutorial lesson, you will first build and analyze binary half adder and full adder circuits made up of logic gates. Then you will create a new database part out of the full adder circuit. Finally, you will use the new full adder part to build a four-bit ripple-carry adder digital circuit.
Building a Ripple-Carry Adder
The following is a list of parts needed for this part of the tutorial lesson:
Digital Inputs: A0, A1, A2 and A3 (keyboard shortcut: N)
Digital Inputs: B0, B1, B2 and B3 (keyboard shortcut: N)
Digital Output: S0, S1, S2 and S3 (keyboard shortcut: O)
Digital Output: Cout (keyboard shortcut: O)
One part of Digital Device MyHA: U1
Three parts of Digital Device MyFA: U2, U3 and U4
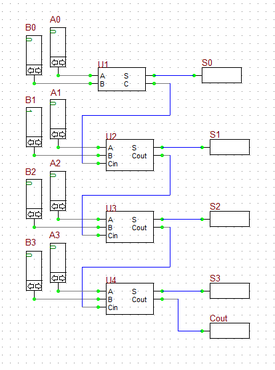
You can use multiple full adders to build an N-bit adder circuit. Each full adder inputs a Cin, which is the Cout of the previous adder. This kind of adder is called a ripple-carry adder, since each carry bit "ripples" to the next full adder. Note that the first (and only the first) full adder may be replaced by a half adder (under the assumption that Cin = 0).
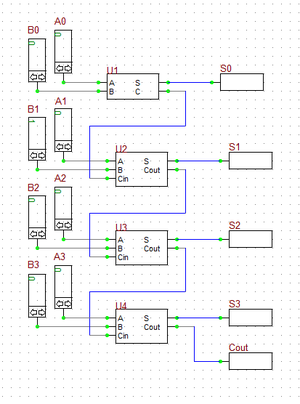
In the last part of this tutorial lesson, you will build a 4-bit ripple-carry binary adder using the half adder and full adder devices you create in the previous parts. Open a new blank project, place all the parted listed above and connect then as shown in the figure. To place your new adder parts, you can either go to the Parts Bin of the Toolbox and search for "MyHA" and "MyFA" alphabetically under the letter "M", or you can open the "Select Device Dialog" by choosing "Select Part..." from the Parts Menu. Note that the half adder block U1 is used for the least significant bits A0 and B0, and the full adder block U2, U3 and U4 are used for the more significant bits. The "Cout" output of the last full adder block U4 summing the most significant bits A4 and B2 is taken out as the "Carry" output of the whole circuit.
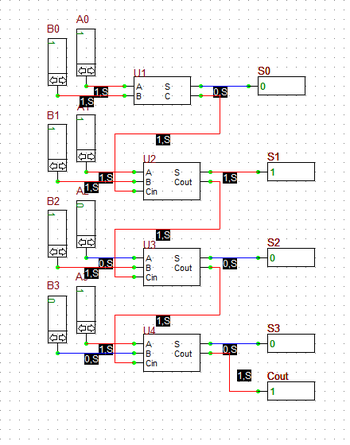
You can run different simulation scenarios by inputting 4-bit binary numbers to A's and B's. The figures below show two of such scenarios. In the figure on the left, A = 1001 (9) and B = 0011 (3). The sum is 1100 representing the decimal number 12. In the figure on the right, A = 1011 (11) and B = 0111 (7). The sum of these inputs must be the decimal number 18, which is equivalent to 0010 with a carry of 1 in a 4-bit system (i.e. 2 + 16), which can be seen in the figure.