What You Will Learn
In this tutorial you will learn how to combine analog and digital devices in the same circuit and perform a mixed-mode simulation of your circuit. You will use DAC and ADC conversion bridges to control the analog voltage levels corresponding to the high and low binary states.
From Digital Devices to Analog Voltages
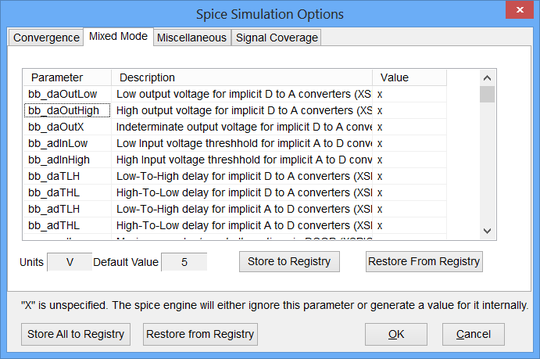
RF.Spice A/D allows you to mix digital and analog devices in the same circuit. To simulate the resulting circuit, the program places implicit A/D or D/A converters in your circuit behind the scenes. By default, it is assumed that the "1" or "High" digital state corresponds to a +5V analog voltage, while the "0" or "Low" digital state corresponds to a 0V analog voltage. You can change these conversion values depending on the type of digital device technology you are using in your circuit. This can be done from the SPICE Simulation Options dialog. You can access this dialog from the Simulate Menu. Under the "Mixed Mode" tab of this dialog, you will see two parameters "bb_daOutLow" and "bb_daOutHigh" in the Parameters table with default values of 0 and 5, respectively. To change these values, click on the parameter value in the rightmost column of the table to highlight it and then type in a new value.
Testing a Simple AND Gate
The following is a list of parts needed for this part of the tutorial lesson:
| Part Name | Part Type | Part Value |
|---|---|---|
| In1 | Digital Input | 1-bit |
| In2 | Digital Input | 1-bit |
| A1 | Generic AND Gate | Defaults |
| R1 - R2 | Resistor | 1k |
| VOUT | Voltage Probe Marker | N/A |
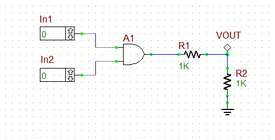
As a first step, let's try out a simple AND gate. Place and connect the parts as shown in the figure below. The two 1k resistors form a voltage divider. The voltage probe marker "VOUT" would provide half the voltage at the output of the AND gate.
Run a live simulation of this circuit and enable circuit animation by clicking the Show Voltage Text ![]() button of the Schematic Editor's Toolbar. When the two inputs are zero or at least one of them is zero, the output voltage is 0V. When both inputs are high, the AND gate's output voltage jumps to +5V and VOUT = 2.5V as can be seen from the figures below.
button of the Schematic Editor's Toolbar. When the two inputs are zero or at least one of them is zero, the output voltage is 0V. When both inputs are high, the AND gate's output voltage jumps to +5V and VOUT = 2.5V as can be seen from the figures below.
Testing a Mixed-Mode Circuit with Conversion Bridges
The following is a list of parts needed for this part of the tutorial lesson:
| Part Name | Part Type | Part Value |
|---|---|---|
| In1 | Digital Input | 1-bit |
| In2 | Digital Input | 1-bit |
| Out1 | Digital Output | N/A |
| A1 | Generic AND Gate | Defaults |
| A2 | Generic OR Gate | Defaults |
| A3 - A4 | 1-Bit DAC Bridge | Defaults, out_high = 3.3 |
| A5 | 1-Bit ADC Bridge | Defaults, in_high = 3 |
| R1 - R2 | Resistor | 1k |
| R3 - R4 | Resistor | 2k |
| R5 - R6 | Resistor | 1k |
| Vcc | DC Bias Voltage Source | 15V |
| Vee | DC Bias Voltage Source | -15V |
| X1 | LM741 Op-Amp | Defaults |
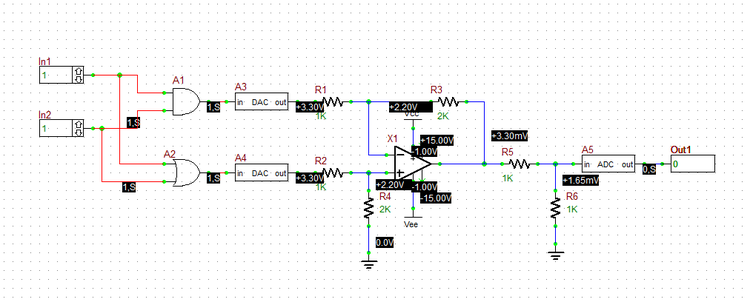
RF.Spice A/D also provides explicit A/D and D/A bridges for conversion between analog and digital signals and vice versa. Using an A/D bridge you can explicitly set the high and low input voltage levels for the input analog signal. Using a D/A bridge you can explicitly set the high and low output voltage levels for the output analog signal. These explicit values will override RF.Spice's default conversion voltage levels set in the SPICE Simulation Options Dialog. Place and connect the parts as shown in the figure below. Vcc and Vee are convenient DC bias voltage sources that you can use in conjunction with Op-Amp devices. Their default values are 5V and -5V, respectively. For this project, you need to change their values to 15V and -15V, respectively.
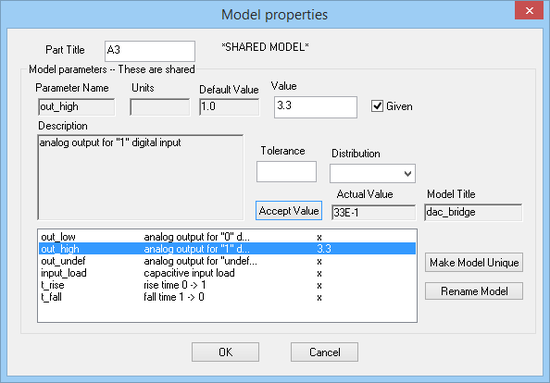
Open the property dialog of the DAC bridge and change the value of the "out_high" parameter to 3.3V. Similarly, change the value of the "in-high" parameter to 3V in the property dialog of the ADC bridge. Note that when you change the properties of the DAC bridge A3, the properties of the DCA bridge A4 change accordingly.
The DAC bridges at the output of the logic gates A1 and A2 produce an analog voltage of 3.3V when the output of the logic gate is at high or "1" state. Let's denote the output voltages of the two DAC bridges A3 and A4 by vi1 and vi2, respectively, denote the output voltage of the Op-Amp X1 by vo1, and denote the input voltage of the ADC bridge A5 by vo2. The Op-Amp circuit is a difference amplifier that you already explored in Analog Tutorial Lesson 6. The resistors R5 and R6 form a simple voltage divider. The following relationship holds:
[math] V_{o1} = \frac{ R_3 }{ R_1} \left( V_{i2} - V_{i1} \right) = 2 \left( V_{i2} - V_{i1} \right) [/math]
[math] V_{o2} = \frac{ R_6 }{ R_5 + R_6} V_{o1} = \frac{1}{2} V_{o1} = V_{i2} - V_{i1} [/math]
From these equations we get the following truth table, which is identical to that of an XOR gate:
| In1 | In2 | vi1 | vi2 | vo1 | vo2 | Out |
|---|---|---|---|---|---|---|
| 0 | 0 | 0V | 0V | 0V | 0V | 0 |
| 0 | 1 | 0V | 3.3V | 6.6V | 3.3V | 1 |
| 1 | 0 | 0V | 3.3V | 6.6V | 3.3V | 1 |
| 1 | 1 | 3.3V | 3.3V | 0V | 0V | 0 |
Run a live simulation of this circuit and enable circuit animation. Change the values of the two digital inputs and verify the above truth table. The figures below show some of these states: