What You Will Learn
In this tutorial you will build and test a high frequency Colpitts oscillator using a parallel resonant LC circuit. The primary objective of this tutorial lesson is to underline the challenges of analyzing oscillator circuits.
Designing a BJT Colpitts Oscillator
The following is a list of parts needed for this part of the tutorial lesson:
| Part Name | Part Type | Part Value |
|---|---|---|
| VCC | Voltage Source | 12V |
| R1 | Resistor | 22k |
| R2 | Resistor | 10k |
| R3 | Resistor | 2k |
| R4 | Resistor | 1k |
| C1 | Capacitor | 100n |
| C2 - C3 | Capacitor | 1n |
| C4 | Capacitor | 27n |
| L1 | Inductor | 27u |
| Q1 | NPN BJT 2N2222 | beta = 150 |
To place the transistor part 2N222, open the "Parts Bin" by selecting the "Add Part" tab of the "Toolbox" on the left side panel. By default, the "Function" tab of the Part Bin is active. This means that parts are sorted based on their function. Open the "Active Components" menu and select the "Transistor..." item and from its submenu select the NPN... item as shown below. All the NPN BJT devices are listed in the Parts Bin. Scroll down the list and find and select “2N2222”. Either double-click the part's name or click the Place Part button at the bottom of the Parts Bin to place the device on your schematic.
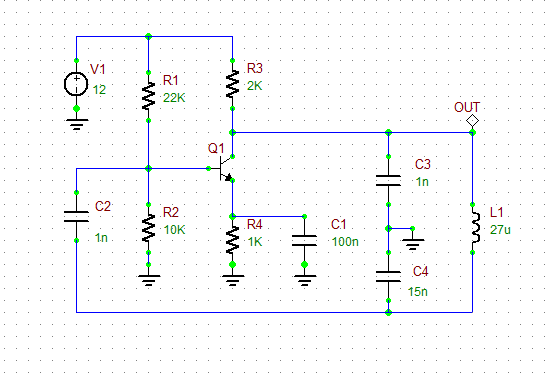
The figure below shows a Colpitts oscillator:
The parallel resonant LC circuit consisting of L1 and capacitors C3 and C4 is connected between the base and the collector of transistor Q1, and partial feedback voltage is fed to its emitter through the voltage divider constituted by C3 and C4. The oscillating frequency of Colpitts oscillator can be calculated from:
[math]f_o = \frac {1}{2 \pi \sqrt{ L_1 \left( \frac{C_3 C_4}{C_3 + C_4} \right) } }[/math]
Note that C1 and C2 are bypass and coupling capacitors, respectively. In this Colpitts oscillator circuit, the feedback factor β(s) is C3/(C3 + C4) ≅ C3/C4. The voltage gain A is given by:
[math]A = g_m R = \frac{I_C}{V_T} R_3 = \frac{kI_C}{qT} R_3[/math]
Therefore, the Barkhausen criterion can be written as:
[math]A \beta(s) = \left( \frac{C_3}{C_3 + C_4} \right). \left( \frac{I_C}{V_T} \right). R_3 \ge 1[/math]
Building & Testing the Colpitts Oscillator
For this project, you will choose L1 = 27μH, C1 = 100nF, C2 = 1nF, C3 = 1nF, C4 = 15nF, R1 = 22k, R2 = 10k, R3 = 2k and R4 = 1k. Place and connect all the parts as shown in the above figure. Place a voltage probe marker at the output of the oscillator circuit at the collector of Q1. For the given inductance and capacitance value, the oscillation frequency of this Colpitts circuit is found to be fo = 1MHz.
Before running a Transient Test of your Colpitts oscillator, first run a DC Bias Test to find the DC operating point of the BJT. The results of the DC bias test are shown in the opposite figure. According to this table, the quiescent collector current IC is 2.985mA. The Barkhausen criterion in this case is thus satisfied:
[math]A \beta(s) = \left( \frac{1nF}{16nF} \right). \left( \frac{2.985\times 10^{-3}}{26\times 10^{-3}} \right). 2\times 10^3 = 14.351 \ge 1[/math]
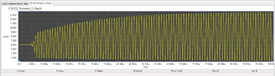
Now run a Transient Test of your oscillator circuit with start and stop times set at 0 and 100μs, respectively, and a Step Ceiling equal to 1ns. The output voltage graph is shown in the figure below. The output signal oscillates between 2V and 14V. A signal period of almost 1μs can be measured, which corresponds to an oscillation frequency of 1MHz.
Changing the Tuning of the Colpitts Oscillator
In this part, let's change the tuning of the parallel LC circuit to get an oscillation frequency of 4MHz. Due to the presence of the square root in the denominator of the formula for fo, you need to make the product of L1 and (C3 || C4) 16 times smaller. To do so, set C3 to 0.25nF and L1 to 6.75μH. Run a new transient test of your modified oscillator with the stop time set to 50μs. As you can see from the figure below, the output voltage this time oscillates between 3V and 11V with a period of about 260ns, which corresponds to an oscillation frequency of 3.85MHz.
Let's see what happen if you try to push the oscillation frequency even higher to 8MHz. For this purpose, let's reduce the value of C3 four times to 62.5pF. Run a new transient test of your oscillator with the stop time set to 50μs. The graph of the output voltage is shown in the figure blow. As you can see, the oscillation breaks down in this case.