Difference between revisions of "Steady-State Thermal Analysis"
Kazem Sabet (Talk | contribs) (→Thermal Boundary Conditions) |
Kazem Sabet (Talk | contribs) |
||
| Line 54: | Line 54: | ||
where Ω is the boundary surface and f(<b>r</b>) is a function. | where Ω is the boundary surface and f(<b>r</b>) is a function. | ||
| + | |||
| + | == The Analogy between Thermal and Electrostatic Equations == | ||
| + | |||
| + | Let us now compare the steady-state thermal Poisson equation to the electrostatic Poisson equation: | ||
| + | |||
| + | <math> \nabla^2 T(\mathbf{r}) = - \frac{w(\mathbf{r})}{k} \quad \Rightarrow \quad \nabla^2 \Phi(\mathbf{r}) = -\frac{\rho(\mathbf{r})}{\epsilon} </math> | ||
| + | |||
| + | |||
| + | |||
| + | It is important to note that there is a one-to-one correspondence between electrostatic and thermal simulation entities: | ||
| + | |||
| + | {| class="wikitable" | ||
| + | |- | ||
| + | ! scope="col"| Electrostatic Item | ||
| + | ! scope="col"| Corresponding Thermal Item | ||
| + | |- | ||
| + | | style="width:200px;" | Electric Scalar Potential | ||
| + | | style="width:200px;" | Temperature | ||
| + | |- | ||
| + | | style="width:200px;" | Electric Field | ||
| + | | style="width:200px;" | Heat Flux Density | ||
| + | |- | ||
| + | | style="width:200px;" | Perfect Electric Conductor | ||
| + | | style="width:200px;" | Perfect Thermal Conductor | ||
| + | |- | ||
| + | | style="width:200px;" | Dielectric Material | ||
| + | | style="width:200px;" | Insulator Material | ||
| + | |- | ||
| + | | style="width:200px;" | Volume Charge | ||
| + | | style="width:200px;" | Volume Heat Source | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
== The Finite Difference Technique == | == The Finite Difference Technique == | ||
Revision as of 00:43, 17 June 2018
Contents
Heat Diffusion Equation
The Fourier law of heat conduction relates the heat transfer rate to the temperature variation:
[math]q = -k\nabla T(\mathbf{r})[/math]
where q is the heat flux density with units of W/m2, T is the temperature expressed in °C or °K, ∇ is the gradient operator and k is the thermal conductivity with units of W/(m.K). It can be shown that the distribution of temperature is governed by the heat diffusion equation subject to the appropriate boundary conditions:
[math] \nabla^2 T(\mathbf{r}) - \frac{1} {\alpha}\frac{\partial T}{\partial t} = \left( \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} + \frac{\partial^2 T}{\partial z^2} \right) - \frac{1} {\alpha}\frac{\partial T}{\partial t} = - \frac{w(\mathbf{r})}{k} [/math]
where α = k/(ρVcp) is the thermal diffusivity with units of m2/s, ρV is the volume mass density, cp is the specific heat capacity of the medium having units of J/(kg.K), and w(r) is the volume heat source density with units of W/m3.
In the steady-state regime, the time derivative vanishes and the diffusion equation reduces to the Poisson equation:
[math] \nabla^2 T(\mathbf{r}) = - \frac{w(\mathbf{r})}{k} [/math]
In a source-free region, the Poisson equation reduces further to the Laplace equation:
[math] \nabla^2 T(\mathbf{r}) = 0 [/math]
The steady-state heat diffusion equations are elliptic partial differential equations. These equations can be solved analytically only for a few canonical geometries with very simple boundary conditions. For most practical and realistic problems, you need to utilize a numerical technique and seek a computer solution. The Poisson and Laplace equations can be solved numerically using the finite difference (FD) method.
Thermal Boundary Conditions
The simplest thermal boundary condition at the walls of the computational domain is the Dirichlet boundary condition:
[math] T(\mathbf{r}) = T_0 [/math]
The Neumann boundary condition constrains the rate of heat flow through the domain boundary walls:
[math]-k \frac{\partial T}{\partial n} = -k \mathbf{\hat{n}} . \nabla T(\mathbf{r}) = q_s [/math]
where qs is the heat flux passing through the boundary walls.
If qs = 0, the Neumann boundary condition is also known as the adiabatic boundary condition, which represents a perfectly insulated surface:
[math]\frac{\partial T}{\partial n} = 0 [/math]
At the interface between the surface of a solid object and air, the convective boundary condition must be enforced:
[math]-k \frac{\partial T}{\partial n} = -h \left[ T(\mathbf{r}) - T_{amb} \right] [/math]
where Tamb is the ambient temperature, and h is the coefficient of convective heat transfer having units of W/(m2.K).
The convective boundary condition is a special case of Robin boundary condition:
[math] \left[ -k \frac{\partial T}{\partial n} + h T(\mathbf{r}) \right]_\Omega = f(\mathbf{r}) [/math]
where Ω is the boundary surface and f(r) is a function.
The Analogy between Thermal and Electrostatic Equations
Let us now compare the steady-state thermal Poisson equation to the electrostatic Poisson equation:
[math] \nabla^2 T(\mathbf{r}) = - \frac{w(\mathbf{r})}{k} \quad \Rightarrow \quad \nabla^2 \Phi(\mathbf{r}) = -\frac{\rho(\mathbf{r})}{\epsilon} [/math]
It is important to note that there is a one-to-one correspondence between electrostatic and thermal simulation entities:
| Electrostatic Item | Corresponding Thermal Item |
|---|---|
| Electric Scalar Potential | Temperature |
| Electric Field | Heat Flux Density |
| Perfect Electric Conductor | Perfect Thermal Conductor |
| Dielectric Material | Insulator Material |
| Volume Charge | Volume Heat Source |
The Finite Difference Technique
The general form of Poisson's equation for any potential ψ can be expressed as:
[math] \frac{\partial^2\psi}{\partial x^2} + \frac{\partial^2\psi}{\partial y^2} + \frac{\partial^2\psi}{\partial z^2} = -f(\mathbf{r}) [/math]
When f(r) = 0, one obtains the well-known Laplace equation, which applies to source-free regions.
The second derivative of ψ with respect to the x coordinate can be approximated by the second-order difference:
[math] \frac{\partial^2\psi(\mathbf{r})}{\partial x^2} \approx \frac{\psi(x+\Delta x,y,z)-2\psi(x,y,z)+\psi(x-\Delta x,y,z)}{(\Delta x)^2} [/math]
Similar expressions can be written for the second derivative with respect to the y and z coordinates.
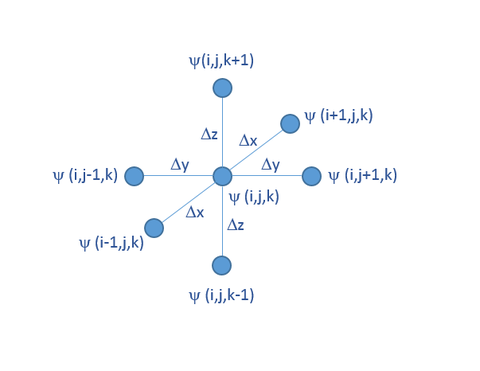
In the finite difference method, the computational domain is discretized using a 3D rectangular grid as shown on the figure below. The grid spacing along the three principal coordinate axes is denoted by Δx, Δy and Δz, respectively. In this grid, the coordinates of any point (x,y,z) in the space can be expressed as x = iΔx, y = jΔy and z = kΔz. Therefore, every point can simply be represented by an index triplet (i,j,k).
The potential at the point (x,y,z) can be expressed in terms of the potentials at its six neighboring grid points along the principal axes. This creates a 7-point computational molecule shown in the figure below:
In the special case of a uniform grid with Δx = Δy = Δz, it can be shown that in a source-free region:
[math] \psi(i,j,k) = \frac{1}{6} \big[ \psi(i+1,j,k) + \psi(i-1,j,k) + \psi(i,j+1,k) + \psi(i,j-1,k) + \psi(i,j,k+1) + \psi(i,j,k-1) \big] [/math]
Two types of domain boundary conditions can be applied:
- Dirichlet boundary condition: ψ = k =const.
- Neumann boundary condition: ∂ψ/∂n = k = const.
In the above, ∂ψ/∂n denotes the normal derivative of the potential at the surface of the domain boundary. EM.Ferma's default domain boundary condition for both the electrostatic and magnetostatic solvers is Dirichlet. At the interface between different material media, additional boundary conditions must be applied. These boundary conditions involve electric or magnetic field components. The field components can be expressed as partial derivatives of the potential, i.e. in the form of ∂ψ/∂x, ∂ψ/∂y or ∂ψ/∂z. Using the respective finite difference approximations of these derivatives, one arrives at fairly complicated difference equations involving the constitutive parameters ε, μ and σ, which must be solved simultaneously with the primary potential difference equations.
Note that the electrostatic Poisson and Laplace equations are of the scalar type, while the magnetostatic Poisson and Laplace equations are vectorial. As a result, the size of the numerical problem in the latter case is three times as large as the former case for the same mesh size.