Difference between revisions of "Glossary of EM.Cube's Sources & Devices"
(→Microstrip Port) |
(→Plane Wave) |
||
| Line 1,062: | Line 1,062: | ||
<td> | <td> | ||
[[Image:Lumped Par_RC.png|thumb|left|480px|The lumped device dialog with the Parallel RC device type selected.]] | [[Image:Lumped Par_RC.png|thumb|left|480px|The lumped device dialog with the Parallel RC device type selected.]] | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
</td> | </td> | ||
</tr> | </tr> | ||
Revision as of 23:45, 16 February 2021
Contents
- 1 Active Distributed One-Port Device
- 2 Active Distributed Two-Port Device
- 3 Active Lumped One-Port Device
- 4 Active Lumped Two-Port Device
- 5 Capacitor
- 6 Coaxial Port
- 7 Coplanar Waveguide (CPW) Port
- 8 Diode
- 9 Distributed Source
- 10 Embedded PEC Via Set
- 11 Fixed-Potential PEC
- 12 Fixed-Temperature PTC
- 13 Hertzian Short Dipole Source
- 14 Impedance Surface
- 15 Impenetrable Surface
- 16 Inductor
- 17 Lumped Source
- 18 Parallel RC Device
- 19 Point Radiator Set
- 20 Point Scatterer Set
- 21 Point Transmitter Set
- 22 Probe Gap Circuit Load
- 23 Probe Gap Circuit Source
- 24 Resistor
- 25 Scattering Wave Port
- 26 Series RL Device
- 27 Slot Trace
- 28 Strip Gap Circuit Load
- 29 Strip Gap Circuit Source
- 30 Thin Wire
- 31 Volume Charge
- 32 Volume Current
- 33 Volume Heat Source
- 34 Waveguide Port
- 35 Wire Current
- 36 Wire Gap Circuit Load
- 37 Wire Gap Circuit Source
Active Distributed One-Port Device
MODULE: EM.Tempo
FUNCTION: Places an active distributed one-port device or circuit with a Netlist definition at an edge of a specified strip object that is parallel to one of the three principal axes
TO DEFINE AN ACTIVE DISTRIBUTED ONE-PORT DEVICE:
- Right-click on the Active One-Ports item in the navigation tree.
- Select Insert New Source... to open up the Active One-Port Device/Circuit Dialog.
- From the Rect Strip drop-down list, select a rectangle strip object. Note that only strip objects parallel to one of the three principal axes are listed.
- Select one of the edges of the rectangle strip where you want to place the active device.
- Enter a value for Height in project units. This is the height of the microstrip transmission line above its ground plane. It determines the size of the "active sheet".
- Enter the Netlist description of the device in the dialog's text editor.
- Alternatively, you can import an existing external Netlist file with a ".CIR" or ".TXT" file extension using the Load Netlist button.
- In the box labeled Input Node, enter the circuit node used in the Netlist that corresponds to the physical microstrip port. The ground is assumed to be Node 0.
- Click the OK button of the dialog to return to the project workspace.
PYTHON COMMAND: distributed_one_port(label,rect_object,height,edge,netlist_filename,input_node)
ACTIVE DISTRIBUTED ONE-PORT DEVICE PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| height | real numeric | project units | 1.5 | the height of the microstrip transmission line above its ground plane |
| input_port | integer numeric | - | 1 | Netlist circuit node that is connected to the FDTD mesh |
Active Distributed Two-Port Device
MODULE: EM.Tempo
FUNCTION: Places an active distributed two-port device or circuit with a Netlist definition at the edges of two specified strip objects that are both parallel to one of the three principal axes
TO DEFINE AN ACTIVE DISTRIBUTED TWO-PORT DEVICE:
- Right-click on the Active Two-Ports item in the navigation tree.
- Select Insert New Source... to open up the Active Two-Port Device/Circuit Dialog.
- In the Input and Output Port sections of the dialog, select two distinct rectangle strip objects from the two Rect Strip drop-down lists. Note that only strip objects parallel to one of the three principal axes are listed.
- Select one of the edges of each rectangle strip where you want to place the input and output ports of the active device.
- Enter a value for Height in project units. This is the height of the two microstrip transmission lines above their common ground plane. It determines the size of the two "active sheets".
- Enter the Netlist description of the two-port device in the dialog's text editor.
- Alternatively, you can import an existing external Netlist file with a ".CIR" or ".TXT" file extension using the Load Netlist button.
- In the boxes labeled Input Node and Output Node, enter the circuit nodes used in the Netlist that corresponds to the two physical microstrip ports. The ground is assumed to be Node 0.
- Click the OK button of the dialog to return to the project workspace.
PYTHON COMMAND: distributed_two_port(label,rect_object_1,height_1,edge_1,rect_object_2,height_2,edge_2,netlist_filename,input_node,output_node)
ACTIVE DISTRIBUTED TWO-PORT DEVICE PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| height_1 | real numeric | project units | 1.5 | the height of the input microstrip transmission line above its ground plane |
| height_2 | real numeric | project units | 1.5 | the height of the output microstrip transmission line above its ground plane |
| input_port | integer numeric | - | 1 | Netlist circuit node that is connected to the FDTD mesh at Port 1 |
| output_port | integer numeric | - | 2 | Netlist circuit node that is connected to the FDTD mesh at Port 2 |
Active Lumped One-Port Device
MODULE: EM.Tempo
FUNCTION: Places a lumped active one-port device or circuit with a Netlist definition at a specified point on a PEC line object that is parallel to one of the three principal axes
TO DEFINE AN ACTIVE LUMPED ONE-PORT DEVICE:
- Right-click on the Lumped Devices item in the navigation tree.
- Select Insert New Source... to open up the Lumped Device Dialog.
- From the Host drop-down list, select a line object. Note that only lines parallel to one of the three principal axes are listed.
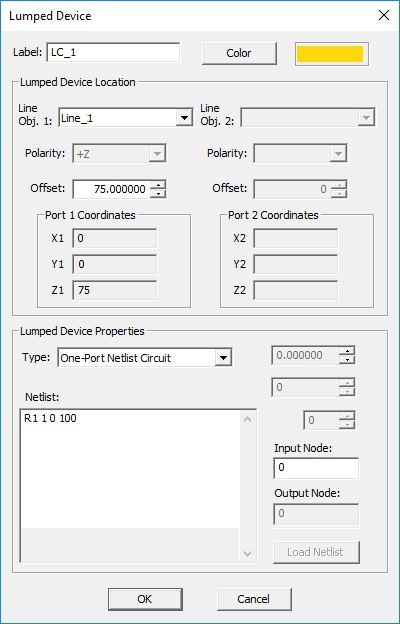
- From the Type drop-down list, select One-Port Netlist Circuit.
- By default, the lumped device is placed at the midpoint of the host line object. You can modify the Offset parameter, which is measured from the start point of the line and is always positive.
- Enter the Netlist definition of your one-port circuit in the box labeled Netlist'.
- Alternatively, you can import a Netlist text file. Click the Load Netlist button of the dialog. The standard Windows Open dialog opens up. You can import text files with a ".CIR" or ".TXT" file extension.
- Enter an integer value for Input Node of your circuit. The device will be connected to the FDTD mesh at the specified input node and the ground node (0).
- Click the OK button of the dialog to return to the project workspace.
PYTHON COMMAND: lumped_one_port(label,line_object,offset,netlist_filename,input_node)
ACTIVE LUMPED ONE-PORT DEVICE PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| offset | real numeric | project units | half the length of host line object | distance between the device and the start point of the host line object |
| input_port | integer numeric | - | 1 | Netlist circuit node that is connected to the FDTD mesh |
Active Lumped Two-Port Device
MODULE: EM.Tempo
FUNCTION: Places a lumped active two-port device or circuit with a Netlist definition at a specified point on a PEC line object that is parallel to one of the three principal axes
TO DEFINE AN ACTIVE LUMPED ONE-PORT DEVICE:
- Right-click on the Lumped Devices item in the navigation tree.
- Select Insert New Source... to open up the Lumped Device Dialog.
- From the Host Obj. 1 drop-down list, select a line object. Note that only lines parallel to one of the three principal axes are listed.
- From the Type drop-down list, select Two-Port Netlist Circuit.
- For a two-port device, you need to select a second host line from the drop-down list labeled Host Obj. 2.
- By default, the lumped device is placed at the midpoint of the host line object. You can modify the two Offset parameters, which are measured from the start point of the host lines and are always positive.
- Enter the Netlist definition of your two-port circuit in the box labeled Netlist'.
- Alternatively, you can import a Netlist text file. Click the Load Netlist button of the dialog. The standard Windows Open dialog opens up. You can import text files with a ".CIR" or ".TXT" file extension.
- Enter two integer values for Input Node' and Output Node of your circuit. The two-pot device will be connected to the FDTD mesh at the specified input and output nodes and the ground node (0).
- Click the OK button of the dialog to return to the project workspace.
PYTHON COMMAND: lumped_two_port(label,line_object_1,offset_1,line_object_2,offset_2,netlist_filename,input_node,output_node)
ACTIVE LUMPED TWO-PORT DEVICE PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| offset1 | real numeric | project units | half the length of host line object | distance between Port 1 and the start point of the first host line object |
| offset2 | real numeric | project units | half the length of host line object | distance between Port 2 and the start point of the second host line object |
| input_port | integer numeric | - | 1 | Netlist circuit node that is connected to the FDTD mesh at Port 1 |
| output_port | integer numeric | - | 2 | Netlist circuit node that is connected to the FDTD mesh at Port 2 |
Capacitor
MODULE: EM.Tempo
FUNCTION: Places a capacitor at a specified point on a PEC line object that is parallel to one of the three principal axes
TO DEFINE A CAPACITOR:
- Right-click on the Lumped Devices item in the navigation tree.
- Select Insert New Source... to open up the Lumped Device Dialog.
- From the Host drop-down list, select a line object. Note that only lines parallel to one of the three principal axes are listed.
- From the Type drop-down list, select Capacitor.
- By default, the lumped device is placed at the midpoint of the host line object. You can modify the Offset parameter, which is measured from the start point of the line and is always positive.
- Enter a value for Capacitance in pF. The default capacitance is 1pF.
- Click the OK button of the dialog to return to the project workspace.
PYTHON COMMAND: capacitor(label,line_object,offset,capacitance_pF)
LUMPED CAPACITOR PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| offset | real numeric | project units | half the length of host line object | distance between the device and the start point of the host line object |
| capacitance | real numeric | pF | 1 | - |
Coaxial Port
MODULE: EM.Tempo
FUNCTION: Places a special distributed circular source of a specified width pointing away radially at one of the bases of a PEC cylinder object that is parallel to one of the three principal axes
TO DEFINE A COAXIAL PORT:
- Right-click on the Coaxial Ports item in the navigation tree of EM.Tempo.
- Select Insert New Source... to open up the Coaxial Port Dialog.
- From the Host drop-down list, select a cylinder object. Note that only PEC cylinder objects parallel to one of the three principal axes are listed.
- You have to specify the outer radius of the coaxial port, which is the same as the outer conductor radius of the coaxial transmission line. The inner conductor radius of the coaxial line is the same as the radius of the host cylinder object.
- A coaxial port can be placed at one of the two bases of the host cylinder. You can select the desired location from the Local Edge drop-down list.
- Click the OK button of the dialog to return to the project workspace.
PYTHON COMMAND: coaxial_src(label,cylinder_object,outer_radius,edge[,magnitude,phase,resistance])
COAXIAL PORT PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| outer radius | real numeric | project units | 2 * host cylinder radius | coaxial line's outer conductor radius |
| resistance | real numeric | Ohms | 50 | internal impedance of the distributed voltage source |
Coplanar Waveguide (CPW) Port
MODULE: EM.Tempo
FUNCTION: Places two coupled special distributed sources of a specified width pointing opposite directions on the two sides of one of the edges of a PEC rectangle strip object that is parallel to one of the three principal planes
TO DEFINE A CPW PORT:
- Right-click on the CPW Ports item in the navigation tree of EM.Tempo.
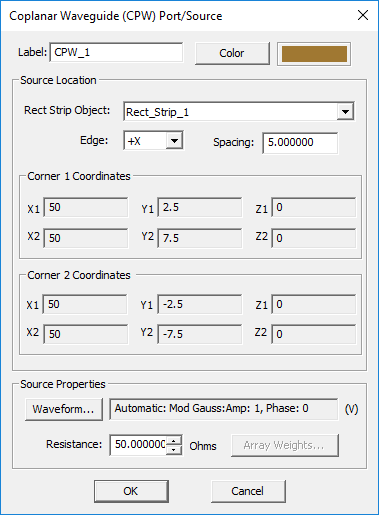
- Select Insert New Source... to open up the CPW Port Dialog.
- From the Host drop-down list, select a rectangle strip object. Note that only PEC rectangle strip objects parallel to one of the three principal planes are listed.
- You have to specify the width of the CPW port, which is the same as the slot width of the coplanar waveguide transmission line.
- A CPW port can be placed at one of the four edges of the host rectangle strip. You can select the desired location from the Edge drop-down list.
- Click the OK button of the dialog to return to the project workspace.
PYTHON COMMAND: cpw_src(label,rect_object,spacing,edge[,magnitude,phase,resistance])
CPW PORT PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| width | real numeric | project units | 5 | coplanar waveguide's slot width |
| resistance | real numeric | Ohms | 50 | internal impedance of the distributed voltage source |
Diode
MODULE: EM.Tempo
FUNCTION: Places an nonlinear diode at a specified point on a PEC line object that is parallel to one of the three principal axes
TO DEFINE A DIODE:
- Right-click on the Lumped Devices item in the navigation tree.
- Select Insert New Source... to open up the Lumped Device Dialog.
- From the Host drop-down list, select a line object. Note that only line parallel to one of the three principal axes are listed.
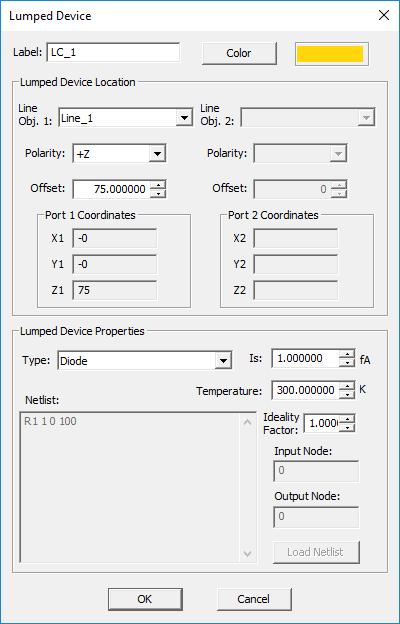
- From the Type drop-down list, select Diode.
- By default, the lumped device is placed at the midpoint of the host line object. You can modify the Offset parameter, which is measured from the start point of the line and is always positive.
- Enter values for Saturation Current in fA, ambient Temperature in degrees Kelvin and a value between 1 and 2 for the diode's Ideality Factor.
- Click the OK button of the dialog to return to the project workspace.
PYTHON COMMAND: inductor(label,line_object,offset,inductance_nH)
LUMPED NONLINEAR DIODE PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| offset | real numeric | project units | half the length of host line object | distance between the device and the start point of the host line object |
| saturation current | real numeric | fA | 1 | - |
| temperature | real numeric | deg K | 300 | - |
| ideality factor | real numeric | - | 1 | must be between 1 and 2 |
Distributed Source
MODULE: EM.Tempo
FUNCTION: Places a distributed voltage source with a distributed internal resistor over a virtual rectangle strip object that is parallel to one of the three principal planes
TO DEFINE A DISTRIBUTED SOURCE:
- Right-click on the Distributed Sources item in the navigation tree of EM.Tempo.
- Select Insert New Source... to open up the Distributed Source Dialog.
- From the Host drop-down list, select a rectangle strip object. Note that only rectangle strip objects of virtual type and parallel to one of the three principal planes are listed.
- A distributed source has a field profile with three options: uniform, sinusoidal and edge-singular. The default option is uniform.
- The direction of the impressed electric field can be aligned along one of the edges of its host rectangle strip object, either in the positive or negative direction. You can select the desired direction from the Field Dir drop-down list.
- Click the OK button of the dialog to return to the project workspace.
NOTES, SPECIAL CASES OR EXCEPTIONS: The current version of EM.Tempo provides three spatial field profiles for a distributed source:
- Uniform: E = E0
- Sinusoidal: E = E0 cos(πy/w)
- Edge-Singular: E = E0 / √ [ 1-(2y/w)^2 ]
In the above functional forms, E0 is a constant, y is the coordinate along the direction of field variation measured from the center of the rectangular area and w is its total width along the y direction.
PYTHON COMMAND: distributed_src(label,rect_object,field_dir,profile[,magnitude,phase,resistance])
DISTRIBUTED SOURCE PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| profile | List: uniform, sinusoidal, edge-singular | V/m | uniform | field distribution profile in the host rectangular region |
| offset | real numeric | project units | half the length of host line object | distance between the source and the start point of the host line object |
| resistance | real numeric | Ohms | 50 | internal impedance of the distributed voltage source |
Embedded PEC Via Set
MODULE: EM.Picasso
FUNCTION: Defines an embedded PEC via object set group
TO DEFINE A PEC VIA SET:
- Right-click on the Embedded Object Sets item in the navigation tree.
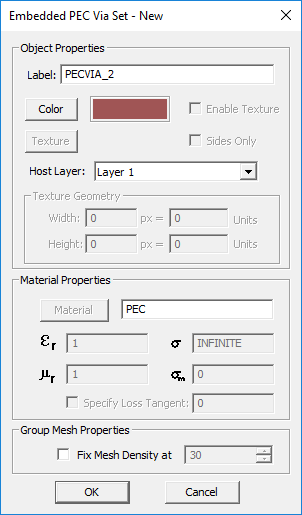
- Select Insert New PEC Via Set... to open up the New PEC Vias Set Dialog.
- From the drop-down list labeled Host Layer, select the substrate layer to embed the new via set.
- Change the color or texture of the via set if desired.
- Click the OK button of the dialog to return to the project workspace.
PYTHON COMMAND:
pec_via_group(label,host_layer)
EMBEDDED PEC VIA SET PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| Locked mesh density | Real Numeric | cells/effective wavelength | 30 | Only if "Lock Mesh" enabled |
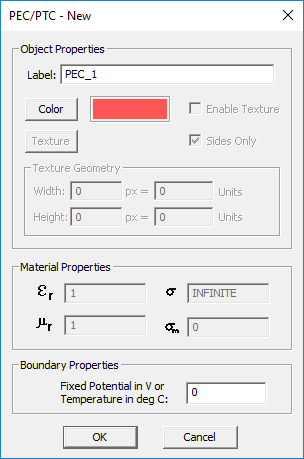
Fixed-Potential PEC
MODULE: EM.Ferma
FUNCTION: Defines an equi-potential perfect electric conductor object group with a specified voltage
TO DEFINE A FIXED-POTENTIAL PEC GROUP:
- Right-click on the Fixed-Potential PEC Objects item in the navigation tree.
- Select Insert New Fixed-Potential PEC... to open up the Fixed-Potential PEC dialog.
- Besides the color and texture properties, you have to enter a value for the fixed Voltage in Volts. The default voltage is 0V.
- Click the OK button of the dialog to return to the project workspace.
PYTHON COMMAND: pec_voltage_group(label,voltage)
FIXED-POTENTIAL PEC PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| voltage | Real Numeric | Volts | 0 | - |
| Locked mesh density | Real Numeric | cells/effective wavelength | 30 | Only if "Lock Mesh" enabled |
Fixed-Temperature PTC
MODULE: EM.Ferma
FUNCTION: Defines an iso-thermal perfect thermal conductor object group with a specified temperature
TO DEFINE A FIXED-TEMPERATURE PTC GROUP:
- Right-click on the Fixed-Temperature PTC Objects item in the navigation tree.
- Select Insert New Fixed-Potential PEC/PTC... to open up the Fixed-Temperature PTC dialog.
- Besides the color and texture properties, you have to enter a value for the fixed Temperature in degrees C. The default voltage is 0°C.
- Click the OK button of the dialog to return to the project workspace.
PYTHON COMMAND: pec_voltage_group(label,voltage)
FIXED-TEMPERATURE PTC PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| temperature | Real Numeric | Deg C | 0 | - |
| Locked mesh density | Real Numeric | cells/effective wavelength | 30 | Only if "Lock Mesh" enabled |
Hertzian Short Dipole Source
MODULE: EM.Tempo, EM.Terrano, EM.Illumina, EM.Picasso, EM.Libera
FUNCTION: Places a short dipole radiator at a specified location in the project workspace
TO DEFINE A SHORT DIPOLE SOURCE:
- Right-click on the Hertzian Short Dipoles item in the navigation tree.
- Select Insert New Source... to open up the Short Dipole Dialog.
- By default, the short dipole radiator is placed at the origin of coordinates. You can modify the source coordinates.
- By default, a vertical Z-directed short dipole radiator is defined. You can change the components of the unit vector along the dipole to reorient it along any arbitrary direction.
- You may also modify the current strength and length of the Hertzian dipole.
- Click the OK button of the dialog to return to the project workspace.
NOTES, SPECIAL CASES OR EXCEPTIONS: A Hertzian dipole is the simplest type of radiator, which consists of a short current element of length Δl, aligned along a unit vector û and carrying a current of I Amperes. The product IΔl is often called the dipole moment and gives a measure of the radiator's strength. A short vertical dipole in the free space generates an azimuth-symmetric, almost omni-directional, far field. The fields radiated by a short Hertzian dipole in a free-space background medium are given by:
- [math] \mathbf{ E^{inc}(r) } = - jk_0 Z_0 (I\Delta l) \left\{ \left[ 1 - \frac{j}{k_0 R} - \frac{1}{(k_0 R)^2} \right] \mathbf{\hat{u}} - \left[ 1 - \frac{3j}{k_0 R} - \frac{3}{(k_0 R)^2} \right] \mathbf{ (\hat{R} \cdot \hat{u}) } \right\} \frac{e^{-jk_0 R}}{4\pi R} [/math]
- [math] \mathbf{ H^{inc}(r) } = - jk_0 (I\Delta l) \left[ 1-\frac{j}{k_0 R} \right] \mathbf{ (\hat{R} \times \hat{u} ) } \frac{e^{-jk_0 R}}{4\pi R} [/math]
where [math] R=|r-r'| \text{, } k_0 = \frac{2\pi}{\lambda_0} \text{ and } Z_0 = 1/Y_0 = \eta_0 [/math], λ0 is the operating wavelength, [math]\mathbf{\hat{u}}[/math] is the unit vector along the dipole, and r0 = (x0, y0, z0) is the position vector of the dipole source.
The radiation resistance of the short dipole is given by:
- [math] R_r = 80\pi^2 \left( \frac{\Delta l}{\lambda_0} \right)^2 [/math]
The radiated power of the short dipole carrying a current I is displayed in the source dialog and is computed as:
- [math] P_{rad} = \frac{1}{2} R_r |I_0|^2 = 40\pi^2 |I|^2 \left( \frac{\Delta l}{\lambda_0} \right)^2 [/math]
The radiated fields of a short dipole above a layered planar background structure are greatly altered by the presence of the substrate layers. The electric and magnetic fields radiated by a short dipole in the presence of a layered background structure are indeed the dyadic Green's functions of that structure:
- [math] \mathbf{E^{inc}(r)} = \int_{\Delta_L} \mathbf{\overline{\overline{G_{EJ}}}(r|r')} \cdot (I\Delta l \mathbf{\hat{u}}) \, dl' [/math]
- [math] \mathbf{H^{inc}(r)} = \int_{\Delta_L} \mathbf{\overline{\overline{G_{HJ}}}(r|r')} \cdot (I\Delta l \mathbf{\hat{u}}) \, dl' [/math]
PYTHON COMMAND: short_dipole(label,x0,y0,z0,length,uX,uY,uZ,amplitude,phase)
SHORT DIPOLE PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| x0 | real numeric | project units | 0 | X-coordinate of source location |
| y0 | real numeric | project units | 0 | Y-coordinate of source location |
| z0 | real numeric | project units | 0 | Z-coordinate of source location |
| amplitude | real numeric | Amperes | 1 | amplitude of dipole current |
| phase | real numeric | degrees | 0 | phase of dipole current |
| length | real numeric | project units | 3 | dipole length |
| uX | real numeric | - | 0 | X-component of unit direction vector |
| uY | real numeric | - | 0 | Y-component of unit direction vector |
| uZ | real numeric | - | 1 | Z-component of unit direction vector |
Impedance Surface
MODULE: EM.Illumina
FUNCTION: Defines an impedance surface object group
TO DEFINE AN IMPEDANCE SURFACE GROUP:
- Right-click on the Impedance Surfaces item in the navigation tree.
- Select Insert New Impedance Surface... to open up the impedance Surface dialog.
- Besides the color and texture properties, you have to enter values for the real and imaginary parts of Surface Impedance. The default values are 0 + j0 Ω, representing a PEC surface.
- Click the OK button of the dialog to return to the project workspace.
NOTES, SPECIAL CASES OR EXCEPTIONS: An impedance surface is a surface on which the tangential electric and magnetic fields are governed by the surface impedance boundary condition (SIBC):
- [math] \mathbf{\hat{n}} \times \mathbf{\hat{n}} \times \mathbf{E} = -Z_s \mathbf{J_s} = -Z_s \mathbf{\hat{n}} \times \mathbf{H} [/math]
where [math]Z_s[/math] is the surface impedance in Ohms and [math]\mathbf{\hat{n}}[/math] is the unit outward normal on the given surface.
PYTHON COMMAND: impedance_surface_group(label,z_real,z_imag)
IMPEDANCE SURFACE PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| resistance | Real Numeric | Ohm | 0.0 | real part of surface impedance |
| reactance | Real Numeric | Ohm | 0.0 | imaginary part of surface impedance |
| Locked mesh density | Real Numeric | cells/effective wavelength | 30 | Only if "Lock Mesh" enabled |
Impenetrable Surface
MODULE: EM.Terrano
FUNCTION: Defines an impenetrable surface block group
TO DEFINE AN IMPENETRABLE SURFACE GROUP:
- Right-click on the Impenetrable Surfaces item in the navigation tree.
- Select Insert New Block... to open up the Impenetrable Surface dialog.
- In the material table, the default setting shows Brick with a relative permittivity of εr = 4.44 and an electric conductivity of σ = 0.001S/m.
- You can change the default material composition by selecting and highlighting it in the table and clicking the Add/Edit button of the dialog.
- In the Material Layer Properties dialog, either enter new values for εr and σ or click the Material button of this dialog to open EM.Cube's Materials List and select one of its entries.
- You can add several layers to your impenetrable surface composition. In that case, you need to define a thickness for each layer. The bottommost layer always has an infinite thickness representing an unbounded half-space medium as seen by an incident ray.
- After you complete the definition of all layers, click the OK button of the dialog to return to the project workspace.
PYTHON COMMAND: impenetrable_surface_group(label,epsilon,sigma[,rr,gg,bb])
IMPENETRABLE SURFACE PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| epsilon | Real Numeric | - | 4.44 | relative permittivity |
| sigma | Real Numeric | S/m | 1e-3 | electric conductivity |
| Locked mesh density | Real Numeric | cells/effective wavelength | 30 | Only if "Lock Mesh" enabled |
Inductor
MODULE: EM.Tempo
FUNCTION: Places an inductor at a specified point on a PEC line object that is parallel to one of the three principal axes
TO DEFINE A INDUCTOR:
- Right-click on the Lumped Devices item in the navigation tree.
- Select Insert New Source... to open up the Lumped Device Dialog.
- From the Host drop-down list, select a line object. Note that only line parallel to one of the three principal axes are listed.
- From the Type drop-down list, select Inductor.
- By default, the lumped device is placed at the midpoint of the host line object. You can modify the Offset parameter, which is measured from the start point of the line and is always positive.
- Enter a value for Inductance in nH. The default inductance is 1nH.
- Click the OK button of the dialog to return to the project workspace.
PYTHON COMMAND: inductor(label,line_object,offset,inductance_nH)
LUMPED INDUCTOR PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| offset | real numeric | project units | half the length of host line object | distance between the device and the start point of the host line object |
| inductance | real numeric | nH | 1 | - |
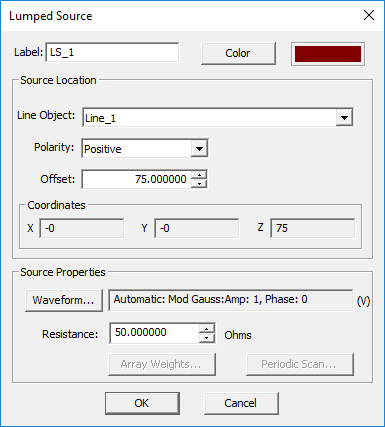
Lumped Source
MODULE: EM.Tempo
FUNCTION: Places an ideal voltage source with a series internal resistor at a specified point on a PEC or thin wire line object that is parallel to one of the three principal axes
TO DEFINE A LUMPED SOURCE:
- Right-click on the Lumped Sources item in the navigation tree.
- Select Insert New Source... to open up the Lumped Source Dialog.
- From the Host drop-down list, select a line object. Note that only line parallel to one of the three principal axes are listed.
- By default, the lumped source is placed at the midpoint of the host line object. You can modify the Offset parameter, which is measured from the start point of the line and is always positive.
- Click the OK button of the dialog to return to the project workspace.
PYTHON COMMAND: lumped_src(label,line_object,offset,polarity[,amplitude,phase,resistance])
LUMPED SOURCE PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| polarity | List: pos, neg | - | - | polarity of the voltage source |
| offset | real numeric | project units | half the length of host line object | distance between the source and the start point of the host line object |
| resistance | real numeric | Ohms | 50 | internal impedance of voltage source at the gap |
Parallel RC Device
MODULE: EM.Tempo
FUNCTION: Places a collocated parallel combination of a resistor and a capacitor at a specified point on a PEC line object that is parallel to one of the three principal axes
TO DEFINE A SERIES RL DEVICE:
- Right-click on the Lumped Devices item in the navigation tree.
- Select Insert New Source... to open up the Lumped Device Dialog.
- From the Host drop-down list, select a line object. Note that only lines parallel to one of the three principal axes are listed.
- From the Type drop-down list, select Parallel RC.
- By default, the lumped device is placed at the midpoint of the host line object. You can modify the Offset parameter, which is measured from the start point of the line and is always positive.
- Enter a value for Resistance in Ohms and a value for Capacitance in pF. The default values are 100Ω and 1pF, respectively.
- Click the OK button of the dialog to return to the project workspace.
PYTHON COMMAND: None
LUMPED PARALLEL RC DEVICE PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| offset | real numeric | project units | half the length of host line object | distance between the device and the start point of the host line object |
| resistance | real numeric | Ohms | 100 | - |
| capacitance | real numeric | pF | 1 | - |
Point Radiator Set
MODULE: EM.Terrano
FUNCTION: Defines a base location set group to be associated with a transmitter or receiver set
TO DEFINE A BASE LOCATION SET GROUP:
- Right-click on the Base Locataions item in the navigation tree.
- Select Insert New Point Set... to open up the base Location Set dialog.
- The only property of a base location set is its color, which you can change from this dialog.
- Click the OK button of the dialog to return to the project workspace.
- By default, the transmitter set is assumed to be made up of vertical half-wave radiators.
- You may also force the transmitters to adjust their Z-coordinates based on the underlying terrain surface.
- Click the OK button of the dialog to return to the project workspace. The new round symbols appear representing the transmitter set.
- You can open the property dialog of the transmitter set and change the radiator type to User Defined Antenna. In that case, click the Import Pattern button of the dialog to set the file path for a far-field radiation pattern data file of ".RAD" type. You can also additionally rotate the imported radiation pattern about its local X-, Y- and Z-axes.
- An imported radiation pattern file typically contains a total radiated power parameter at its file header. By default, this value is overridden and the Custom Power check box is checked. A default total power of 1W is assigned to each transmitter, which you can change to any arbitrary value. Or you may uncheck Custom Power to use the imported value of the total radiated power.
PYTHON COMMAND radiator_custom_group(label,pattern_file,rot_x,rot_y,rot_z,rr,gg,bb)
POINT RADIATOR SET PARAMETERS:
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| radiator type | options: vertical half-wave dipole, user define antenna | - | vertical half-wave dipole | - |
| pattern file | file path | - | Models\DPL_STD.RAD | imported far-field radiation pattern data file with a ".RAD" file extension for the case of user defined antenna |
| rot_x | real numeric | degrees | 0 | additional rotation angle of the imported radiation pattern about the local X-axis |
| rot_y | real numeric | degrees | 0 | additional rotation angle of the imported radiation pattern about the local Y-axis |
| rot_z | real numeric | degrees | 0 | additional rotation angle of the imported radiation pattern about the local Z-axis |
Point Scatterer Set
MODULE: EM.Terrano
FUNCTION: Defines a point scatterer set group to be used as one or more targets in a radar simulation
TO DEFINE A POINT SCATTERER SET GROUP:
- Right-click on the Point Scatterers item in the navigation tree.
- Select Insert New Scatterer Set... to open up the Point Scatterer Set dialog.
- You can change the color of the scatterer set from this dialog.
- In the section titled "Polarimetric Scattering Matrix Data File", use the Import... button to browse the folder on your computer. Clicking the Import... button opens the Windows Explorer window. Select a file with a ".DAT" file extension, whose name ends in polar_scat.
- Click the OK button of the dialog to return to the project workspace.
PYTHON COMMAND: scatterer_group(label,polar_scat_file[,rr,gg,bb])
POINT SCATTERER SET PARAMETERS:
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| scattering matrix file | file path | - | Models\POLAR_SCAT.DAT | imported polarimetric scattering matrix data file with a ".DAT" file extension and a name ending in "polar_scat" |
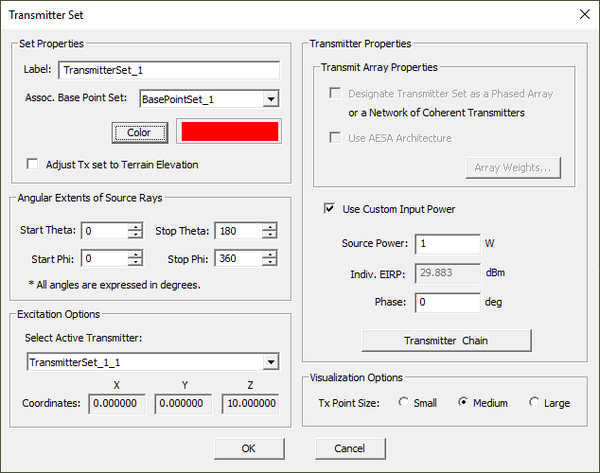
Point Transmitter Set
MODULE: EM.Terrano
FUNCTION: Defines an transmitter set associated with an existing base location set
TO DEFINE A POINT TRANSMITTER SET:
- Right-click on the Transmitters item in the navigation tree of EM.Terrano.
- Select Insert New Transmitter Set... to open up the Transmitter Set Dialog.
- From the drop-down list labeled Select Base Point Set, choose the desired base location set, which can be a single point object or a point array.
PYTHON COMMAND transmitter_set(label,radiator_set[,power,phase,rin_ant,xin_ant])
POINT TRANSMITTER SET PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| baseband power | real numeric | Watts | 1 | total transmitted power |
| phase | real numeric | degrees | 0 | phase of transmitted signal |
Probe Gap Circuit Load
MODULE: EM.Picasso
FUNCTION: Places a general series-parallel RLC circuit in the middle of an embedded vertical PEC via object
TO DEFINE A PROBE GAP CIRCUIT:
- Right-click on the Probe Gap Circuits item in the navigation tree.
- Select Insert New Source... to open up the Lumped Device Dialog.
- From the Host drop-down list, select a PEC Via object set.
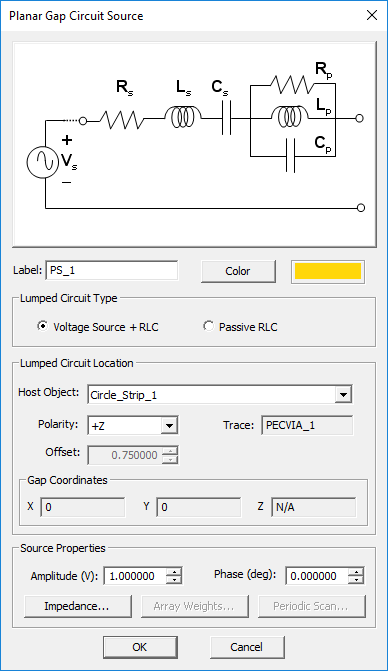
- For "Lumped Circuit Type", select the Passive RLC radio button.
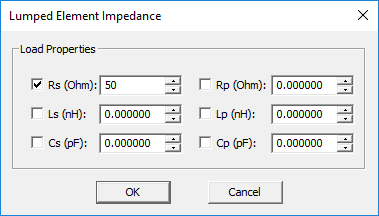
- Click the Impedance... button of the dialog to open up the Lumped Element Impedance dialog. The default series resistance is 50Ω. Check all the boxes for the series or parallel R, L, C elements as desired and enter values for the resistances, capacitances and inductances.
- Click the OK buttons of the dialogs to return to the project workspace.
PYTHON COMMAND: (Only a series resistor when amplitude is set equal to zero.)
probe_src(label,via_object,polarity[,amplitude,phase,resistance])
PROBE GAP LOAD PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| Rs | real numeric | Ohms | 50 | series resistor (must be checked) |
| Ls | real numeric | nH | - | series inductor (must be checked) |
| Cs | real numeric | pF | - | series capacitor (must be checked) |
| Rs | real numeric | Ohms | - | parallel resistor (must be checked) |
| Ls | real numeric | nH | - | parallel inductor (must be checked) |
| Cs | real numeric | pF | - | parallel capacitor (must be checked) |
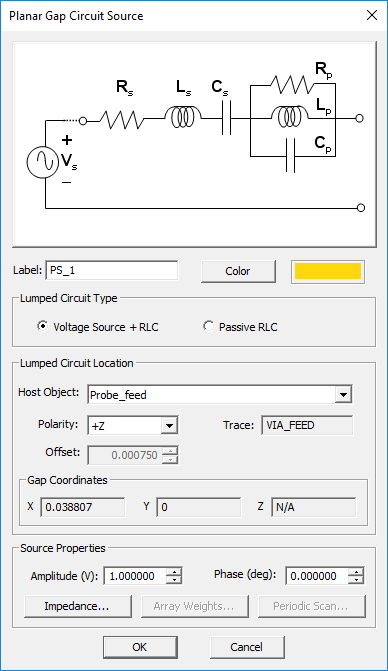
Probe Gap Circuit Source
MODULE: EM.Picasso
FUNCTION: Creates an infinitesimal gap across the middle of a vertical PEC via object and places an ideal voltage source with a series internal resistor
TO DEFINE A PROBE GAP SOURCE:
- Right-click on the Probe Gap Circuits item in the navigation tree.
- Select Insert New Source... to open up the Probe Gap Source Dialog.
- From the Host drop-down list, select a PEC via object.
- The probe gap source is always placed in the middle of the PEC via object.
- Click the OK button of the dialog to return to the project workspace.
PYTHON COMMAND: probe_src(label,via_object,polarity[,amplitude,phase,resistance])
PROBE GAP SOURCE PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| polarity | List: pos, neg | - | pos | polarity of the voltage source |
| amplitude | real numeric | Volts | 1 | amplitude of voltage source at the gap |
| phase | real numeric | degrees | 0 | phase of voltage source at the gap |
Resistor
MODULE: EM.Tempo
FUNCTION: Places a resistor at a specified point on a PEC line object that is parallel to one of the three principal axes
TO DEFINE A RESISTOR:
- Right-click on the Lumped Devices item in the navigation tree.
- Select Insert New Source... to open up the Lumped Device Dialog.
- From the Host drop-down list, select a line object. Note that only line parallel to one of the three principal axes are listed.
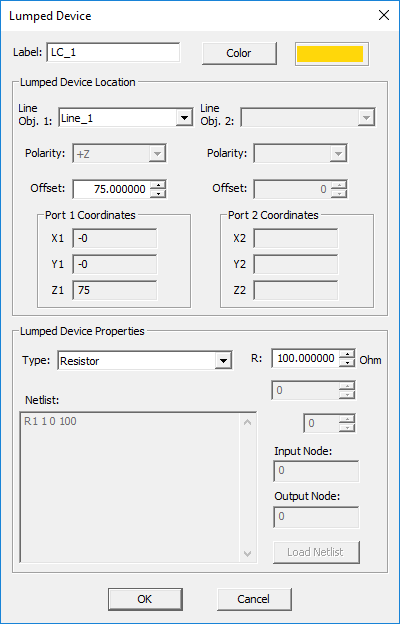
- From the Type drop-down list, select Resistor.
- By default, the lumped device is placed at the midpoint of the host line object. You can modify the Offset parameter, which is measured from the start point of the line and is always positive.
- Enter a value for Resistance in Ohms. The default resistance is 100Ω.
- Click the OK button of the dialog to return to the project workspace.
PYTHON COMMAND: resistor(label,line_object,offset,resistance)
LUMPED RESISTOR PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| offset | real numeric | project units | half the length of host line object | distance between the device and the start point of the host line object |
| resistance | real numeric | Ohms | 50 | - |
Scattering Wave Port
MODULE: EM.Picasso
FUNCTION: Creates an infinitesimal gap across a PEC rectangle strip object at a specified location and places an ideal voltage source with a series internal resistor
TO DEFINE A SCATTERING WAVE PORT:
- Right-click on the Scattering Wave Ports item in the navigation tree.
- Select Insert New Source... to open up the Wave Port Dialog.
- From the Host drop-down list, select a PEC rectangle strip object.
- By default, the wave port is placed at one end of the host rect strip object. The incident wave propagates along the host strip towards this end. You can change the direction of the incident wave. You can also modify the Offset parameter, which is measured from the endpoint of the host strip. This establishes the phase reference plane for computation of the scattering parameters.
- Click the OK button of the dialog to return to the project workspace.
NOTES, SPECIAL CASES OR EXCEPTIONS: A scattering wave port is made up of a gap source that is placed close to an open end of a rectangle strip representing a feed line. The other end of the line is typically connected to a planar structure of interest. in the process of planar mesh generation, EM.Picasso automatically extends the length of a port line that hosts a scattering wave port to about two effective wavelengths. This is done to provide enough length for formation of a clean standing wave current pattern. The effective wavelength of a transmission line for length extension purposes is calculated in a similar manner as for the planar mesh resolution. It is defined as [math]\lambda_{eff} = \tfrac{\lambda_0}{\sqrt{\varepsilon_{eff}}}[/math], where εeff is the effective permittivity. For metal and conductive sheet traces, the effective permittivity is defined as the larger of the permittivities of the two substrate layers just above and below the metallic trace. For slot traces, the effective permittivity is defined as the mean (average) of the permittivities of the two substrate layers just above and below the metallic trace. The host port line must always be open from one end to allow for its length extension. You have to make sure that there are no objects standing on the way of the extended port line to avoid any unwanted overlaps.
PYTHON COMMAND: wave_port(label,rect_object,offset,is_negative[,amplitude,phase])
SCATTERING WAVE PORT PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| direction | List: pos, neg | - | pos | direction of the incident wave |
| offset | real numeric | project units | 0 | distance between the source and the endpoint of the host strip object |
| amplitude | real numeric | Volts | 1 | amplitude of incident wave |
| phase | real numeric | degrees | 0 | phase of incident wave |
RELATED LINKS: Calculating Scattering Parameters Using Prony's Method
Series RL Device
MODULE: EM.Tempo
FUNCTION: Places a collocated series combination of a resistor and an inductor at a specified point on a PEC line object that is parallel to one of the three principal axes
TO DEFINE A SERIES RL DEVICE:
- Right-click on the Lumped Devices item in the navigation tree.
- Select Insert New Source... to open up the Lumped Device Dialog.
- From the Host drop-down list, select a line object. Note that only lines parallel to one of the three principal axes are listed.
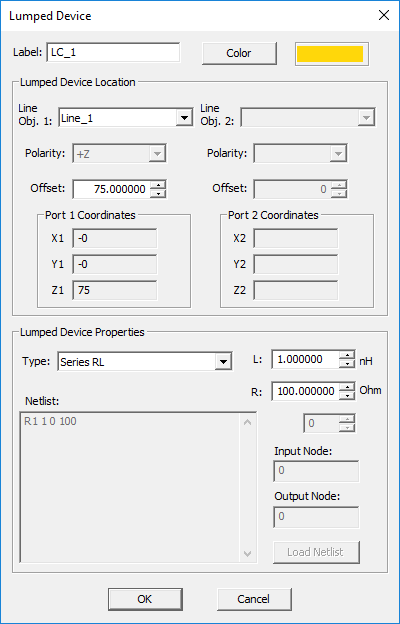
- From the Type drop-down list, select Series RL.
- By default, the lumped device is placed at the midpoint of the host line object. You can modify the Offset parameter, which is measured from the start point of the line and is always positive.
- Enter a value for Resistance in Ohms and a value for Inductance in nH. The default values are 100Ω and 1nF, respectively.
- Click the OK button of the dialog to return to the project workspace.
PYTHON COMMAND: None
LUMPED SERIES RL DEVICE PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| offset | real numeric | project units | half the length of host line object | distance between the device and the start point of the host line object |
| resistance | real numeric | Oms | 100 | |
| inductance | real numeric | nH | 1 | - |
Slot Trace
MODULE: EM.Picasso
FUNCTION: Defines a slot trace object group on an infinite PEC ground plane
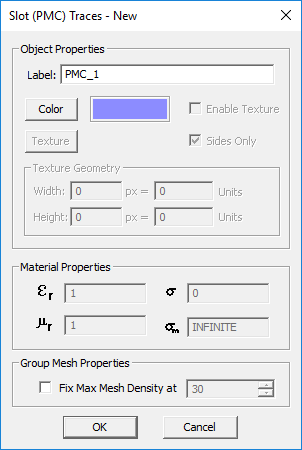
TO DEFINE A SLOT TRACE GROUP:
- Right-click on the Slot Traces item in the navigation tree.
- Select Insert New Slot Trace... to open up the New Slot Trace dialog.
- The only properties of a slot trace group you can modify is its color and texture.
- Click the OK button of the dialog to return to the project workspace.
PYTHON COMMAND: slot_group(label)
SLOT TRACE PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| Locked mesh density | Real Numeric | cells/effective wavelength | 30 | Only if "Lock Mesh" enabled |
Strip Gap Circuit Load
MODULE: EM.Oicasso, EM.Libera
FUNCTION: Places a general series-parallel RLC circuit at a specified point on a PEC rectangle strip object
TO DEFINE A STRIP GAP CIRCUIT:
- Right-click on the Strip Gap Circuits item in the navigation tree.
- Select Insert New Source... to open up the Lumped Device Dialog.
- From the Host drop-down list, select a rectangle strip object.
- For "Lumped Circuit Type", select the Passive RLC radio button.
- By default, the lumped device is placed at the midpoint of the host rectangle strip object. You can modify the Offset parameter, which is measured from the center of the strip and can be either positive or negative.
- Click the Impedance... button of the dialog to open up the Lumped Element Impedance dialog. The default series resistance is 50Ω. Check all the boxes for the series or parallel R, L, C elements as desired and enter values for the resistances, capacitances and inductances.
- Click the OK buttons of the dialogs to return to the project workspace.
PYTHON COMMAND: (Only a series resistor when amplitude is set equal to zero.)
rect_gap_src(label,rect_object,offset,polarity[,amplitude,phase,resistance])
STRIP GAP LOAD PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| offset | real numeric | project units | half the length of host rectangle strip object | distance between the device and the center of the host strip object |
| Rs | real numeric | Ohms | 50 | series resistor (must be checked) |
| Ls | real numeric | nH | - | series inductor (must be checked) |
| Cs | real numeric | pF | - | series capacitor (must be checked) |
| Rs | real numeric | Ohms | - | parallel resistor (must be checked) |
| Ls | real numeric | nH | - | parallel inductor (must be checked) |
| Cs | real numeric | pF | - | parallel capacitor (must be checked) |
Strip Gap Circuit Source
MODULE: EM.Picasso, EM.Libera
FUNCTION: Creates an infinitesimal gap across a PEC rectangle strip object at a specified location and places an ideal voltage source with a series internal resistor
TO DEFINE A STRIP GAP SOURCE:
- Right-click on the Strip Gap Circuits item in the navigation tree.
- Select Insert New Source... to open up the Strip Gap Source Dialog.
- From the Host drop-down list, select a PEC rectangle strip object.
- By default, the strip gap source is placed at the midpoint of the host rect strip object. You can modify the Offset parameter, which is measured from the midpoint of the host strip and can be either positive or negative.
- Click the OK button of the dialog to return to the project workspace.
PYTHON COMMAND: rect_gap_src(label,rect_object,offset,polarity[,amplitude,phase,resistance])
STRIP GAP SOURCE PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| polarity | List: pos, neg | - | pos | polarity of the voltage source |
| offset | real numeric | project units | 0 | distance between the source and the midpoint of the host strip object |
| amplitude | real numeric | Volts | 1 | amplitude of voltage source at the gap |
| phase | real numeric | degrees | 0 | phase of voltage source at the gap |
Thin Wire
FUNCTION: Defines a thin wire object group with a specified wire radius
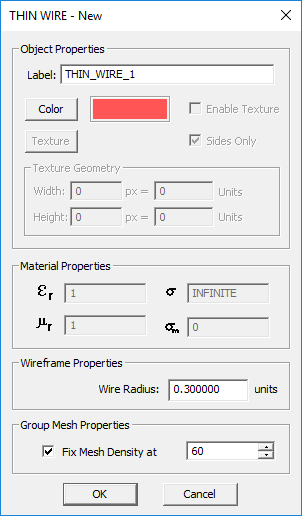
TO DEFINE A THIN WIRE GROUP:
- Right-click on the Thin Wires item in the navigation tree.
- Select Insert New Thin Wire... to open up the Thin Wire dialog.
- Enter a value for the Wire Radius.
- Click the OK button of the dialog to return to the project workspace.
PYTHON COMMAND: thinwire_group(label,radius)
THIN WIRE PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| Wire radius | Real Numeric | project units | 0.3 | - |
| Locked mesh density | Real Numeric | cells/effective wavelength | 50 | "Lock Mesh" enabled by default |
Volume Charge
MODULE: EM.Ferma
FUNCTION: Defines a volume charge source group with a specified charge density
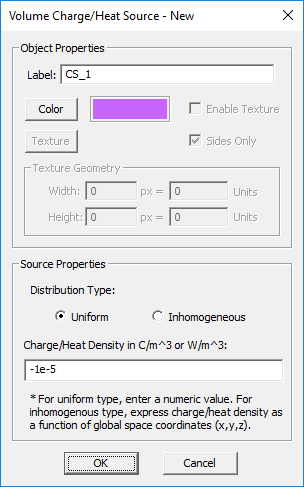
TO DEFINE A VOLUME CHARGE GROUP:
- Right-click on the Volume Charges item in the navigation tree.
- Select Insert New Volume Charge... to open up the Volume Charge Source dialog.
- You have two options to choose from: Uniform and Inhomogeneous.
- If you choose the uniform option, you have to enter a numeric value for Charge Density in C/m^3.
- If you choose the inhomogeneous option, you have to enter an expression for Charge Density in the global (x,y,z) coordinates.
- Click the OK button of the dialog to return to the project workspace.
PYTHON COMMAND: charge_group(label,density)
VOLUME CHARGE PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| density | Real Numeric | C/m^3 | -1e-5 | volume charge density with a positive or negative sign |
Volume Current
MODULE: EM.Ferma
FUNCTION: Defines a volume current source group with a specified current density vector
TO DEFINE A VOLUME CURRENT GROUP:
- Right-click on the Volume Currents item in the navigation tree.
- Select Insert New Volume Current... to open up the Volume Current Source dialog.
- You have two options to choose from: Uniform and Inhomogeneous.
- If you choose the uniform option, you have to enter three numeric values for the three components of volume current density Jx, Jy and Jz in A/m^2.
- If you choose the inhomogeneous option, you have to enter three expressions for the three components of volume current density Jx, Jy and Jz in the global (x,y,z) coordinates.
- Click the OK button of the dialog to return to the project workspace.
PYTHON COMMAND: volume_current_group(label,Jx,Jy,Jz)
VOLUME CURRENT PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| Jx | Real Numeric | A/m^2 | 0.0 | X-component of volume current density vector |
| Jy | Real Numeric | A/m^2 | 0.0 | Y-component of volume current density vector |
| Jz | Real Numeric | A/m^2 | 1.0 | Z-component of volume current density vector |
Volume Heat Source
MODULE: EM.Ferma
FUNCTION: Defines a volume heat source group with a specified heat density
TO DEFINE A VOLUME HEAT SOURCE GROUP:
- Right-click on the Volume Heat Sources item in the navigation tree.
- Select Insert New Volume Heat Source... to open up the Volume Heat Source dialog.
- You have two options to choose from: Uniform and Inhomogeneous.
- If you choose the uniform option, you have to enter a numeric value for Heat Density in W/m^3.
- If you choose the inhomogeneous option, you have to enter an expression for Heat Density in the global (x,y,z) coordinates.
- Click the OK button of the dialog to return to the project workspace.
PYTHON COMMAND: charge_group(label,density)
VOLUME HEAT SOURCE PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| density | Real Numeric | W/m^3 | -1e-5 | volume heat density with a positive or negative sign |
Waveguide Port
MODULE: EM.Tempo
FUNCTION: Places a TE10 modal source at a specified location across a hollow PEC box object that is parallel to one of the three principal axes
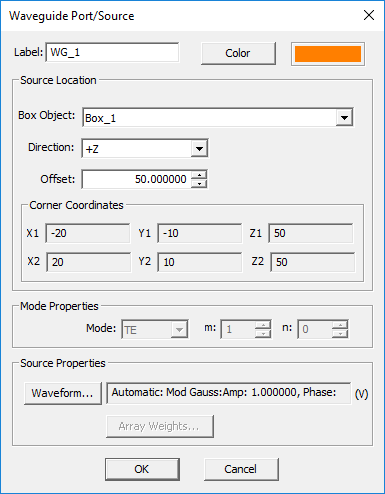
TO DEFINE A WAVEGUIDE PORT:
- Right-click on the Waveguide Ports item in the navigation tree of EM.Tempo.
- Select Insert New Source... to open up the Waveguide Port Dialog.
- From the Host drop-down list, select a box object. Note that only hollow PEC box objects parallel to one of the three principal axes are listed.
- By default, the waveguide port is placed in the middle of the host box object parallel to its base. You can modify the Offset parameter, which is measured from the bottom base of the box.
- Click the OK button of the dialog to return to the project workspace.
PYTHON COMMAND: waveguide_src(label,box_object,offset,is_negative[,amplitude,phase])
WAVEGUIDE PORT PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| direction | List: pos, neg | - | - | direction of incident wave propagation |
| offset | real numeric | project units | half the height of host box object | distance between the source and the bottom base of the host box object |
Wire Current
MODULE: EM.Ferma
FUNCTION: Defines a wire current source group with a specified current and wire radius
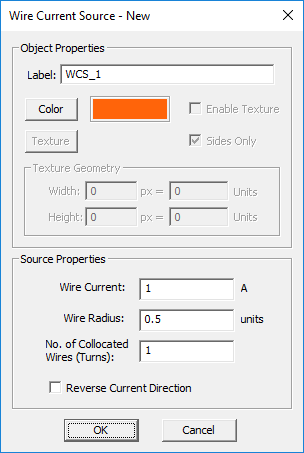
TO DEFINE A WIRE CURRENT GROUP:
- Right-click on the Wire Current item in the navigation tree.
- Select Insert New Wire Current... to open up the Wire Current dialog.
- Enter a value for the total Current flowing in the wire in Amperes as well as a value for Wire Radius in the project units.
- You may assume that the wire current consists of multiple turns or multiple bundled wires. The default number of turns is 1, but you can change it.
- The current flowing in the wire is directional. You may need to check the box labeled Reverse Current if you prefer the opposite direction.
- Click the OK button of the dialog to return to the project workspace.
NOTES, SPECIAL CASES OR EXCEPTIONS: EM.Ferma allows you to define idealized wire current sources. You can use this source type to model filament currents or coils. Wire currents are defined using only line and polyline objects. You also need to define a current value I in Amperes and a wire radius r in the project units. The line or polyline object is then approximated as a volume current with a current density of J = I/(πr2) flowing along the line or polyline side's direction.
| |
If you draw curve CAD objects under a wire current group, they will be permanently converted to polyline objects before running the simulation engine. |
PYTHON COMMAND: wire_current_group(label,current,wire_radius)
WIRE CURRENT PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| current | Real Numeric | A | 1.0 | total current flowing through the wire |
| wire_radius | Real Numeric | project units | 0.5 | - |
| wire_count | Integer Numeric | - | 1 | number of collocated wires or loop turns |
Wire Gap Circuit Load
MODULE: EM.Libera
FUNCTION: Places a general series-parallel RLC circuit at a specified point on a PEC line object
TO DEFINE A WIRE GAP CIRCUIT:
- Right-click on the Wire Gap Circuits item in the navigation tree.
- Select Insert New Source... to open up the Lumped Device Dialog.
- From the Host drop-down list, select a line object.
- For "Lumped Circuit Type", select the Passive RLC radio button.
- By default, the lumped device is placed at the midpoint of the host line object. You can modify the Offset parameter, which is measured from the start point of the line and is always positive.
- Click the Impedance... button of the dialog to open up the Lumped Element Impedance dialog. The default series resistance is 50Ω. Check all the boxes for the series or parallel R, L, C elements as desired and enter values for the resistances, capacitances and inductances.
- Click the OK buttons of the dialogs to return to the project workspace.
PYTHON COMMAND: (Only a series resistor when amplitude is set equal to zero.)
wire_gap_src(label,line_object,offset,polarity[,amplitude,phase,resistance])
WIRE GAP LOAD PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| offset | real numeric | project units | half the length of host line object | distance between the device and the start point of the host line object |
| Rs | real numeric | Ohms | 50 | series resistor (must be checked) |
| Ls | real numeric | nH | - | series inductor (must be checked) |
| Cs | real numeric | pF | - | series capacitor (must be checked) |
| Rs | real numeric | Ohms | - | parallel resistor (must be checked) |
| Ls | real numeric | nH | - | parallel inductor (must be checked) |
| Cs | real numeric | pF | - | parallel capacitor (must be checked) |
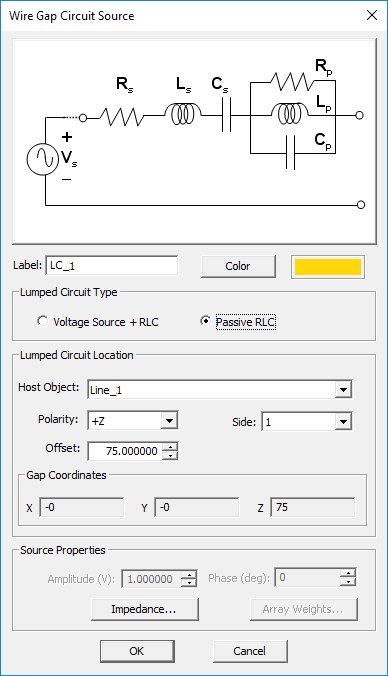
Wire Gap Circuit Source
MODULE: EM.Libera
FUNCTION: Creates an infinitesimal gap across a PEC or thin wire line object at a specified location and places an ideal voltage source with a series internal resistor
TO DEFINE A WIRE GAP SOURCE:
- Right-click on the Wire Gap Circuits item in the navigation tree.
- Select Insert New Source... to open up the Wire Gap Source Dialog.
- From the Host drop-down list, select a PEC or thin wire line object.
- By default, the wire gap source is placed at the midpoint of the host line object. You can modify the Offset parameter, which is measured from the start point of the host line and is always positive.
- Click the OK button of the dialog to return to the project workspace.
PYTHON COMMAND: wire_gap_src(label,line_object,offset,polarity[,amplitude,phase,resistance])
WIRE GAP SOURCE PARAMETERS
| Parameter Name | Value Type | Units | Default Value | Notes |
|---|---|---|---|---|
| polarity | List: pos, neg | - | pos | polarity of the voltage source |
| offset | real numeric | project units | 0 | distance between the source and the start point of the host line object |
| amplitude | real numeric | Volts | 1 | amplitude of voltage source at the gap |
| phase | real numeric | degrees | 0 | phase of voltage source at the gap |