Difference between revisions of "Steady-State Thermal Analysis"
Kazem Sabet (Talk | contribs) (→Heat Diffusion Equation) |
Kazem Sabet (Talk | contribs) (→Heat Diffusion Equation) |
||
| Line 13: | Line 13: | ||
where q is the heat transfer rate or heat flux density with units of W/m<sup>2</sup>, T is the temperature expressed in °C or °K, ∇ is the gradient operator and k is the thermal conductivity with units of W/(m.K). It can be shown that the distribution of temperature is governed by the heat diffusion equation subject to the appropriate boundary conditions: | where q is the heat transfer rate or heat flux density with units of W/m<sup>2</sup>, T is the temperature expressed in °C or °K, ∇ is the gradient operator and k is the thermal conductivity with units of W/(m.K). It can be shown that the distribution of temperature is governed by the heat diffusion equation subject to the appropriate boundary conditions: | ||
| − | <math> \frac{\partial T}{\partial t} - \alpha \nabla^2 T(\mathbf{r}) = \frac{\partial T}{\partial t} - \alpha \left( \frac{\partial^2 | + | <math> \frac{\partial T}{\partial t} - \alpha \nabla^2 T(\mathbf{r}) = \frac{\partial T}{\partial t} - \alpha \left( \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} + \frac{\partial^2 T}{\partial z^2} \right) = 0 </math> |
| − | + | where α is the thermal diffusivity with units of W/m. | |
| − | where & | + | |
Revision as of 18:54, 16 June 2018
Contents
- 1 Heat Diffusion Equation
- 2 Electrostatics Analysis
- 3 The Solution of Poisson's Equation
- 4 Free-Space Electric Field and Scalar Potential
- 5 Static Fields Arising from Steady-State Conduction Currents
- 6 Magnetostatics Analysis
- 7 Free-Space Magnetic Field and Vector Potential
- 8 The Finite Difference Technique
- 9 2D Quasi-Static Solution of TEM Transmission Line Structures
Heat Diffusion Equation
The Fourier law of heat conduction relates the heat flux to temperature variations:
[math]q = -k\nabla T(\mathbf{r})[/math]
where q is the heat transfer rate or heat flux density with units of W/m2, T is the temperature expressed in °C or °K, ∇ is the gradient operator and k is the thermal conductivity with units of W/(m.K). It can be shown that the distribution of temperature is governed by the heat diffusion equation subject to the appropriate boundary conditions:
[math] \frac{\partial T}{\partial t} - \alpha \nabla^2 T(\mathbf{r}) = \frac{\partial T}{\partial t} - \alpha \left( \frac{\partial^2 T}{\partial x^2} + \frac{\partial^2 T}{\partial y^2} + \frac{\partial^2 T}{\partial z^2} \right) = 0 [/math]
where α is the thermal diffusivity with units of W/m.
Under the static assumptions, Maxwell's equations reduce to elliptic partial differential equations known as the Poisson and Laplace equations. These equations can be solved analytically only for a few canonical geometries with very simple boundary conditions. For most practical and realistic problems, you need to utilize a numerical technique and seek a computer solution. The Poisson and Laplace equations can be solved numerically using the finite difference (FD) method.
Electrostatics Analysis
At very low frequencies, as ω→0 and k→0, the Helmholtz equation for the electric scalar potential reduces to the Poisson equation subject to specified boundary conditions:
[math]\Delta\Phi(\mathbf{r}) = \nabla^2 \Phi(\mathbf{r}) = -\frac{\rho(\mathbf{r})}{\epsilon}[/math]
where Φ(r) is the electric scalar potential expressed in Volts [v], ρ(r) is the volume charge density expressed in C/m3, and ε = εr ε0 is the permittivity of the medium having the units of F/m.
The electric field boundary conditions at the interface between two material media are:
[math] \hat{\mathbf{n}} . [ \mathbf{D_2(r)} - \mathbf{D_1(r)} ] = \rho_s (\mathbf{r}) [/math]
[math] \hat{\mathbf{n}} \times [ \mathbf{E_2(r)} - \mathbf{E_1(r)} ] = 0 [/math]
where [math] \hat{\mathbf{n}} [/math] is the unit normal vector at the interface pointing from medium 1 towards medium 2, D(r) = εE(r) is the electric flux density expressed in C/m2, E(r) is the electric field vector expressed in V/m, and ρs is the surface charge density at the interface having the units of expressed in C/m2.
In a source-free region, ρ(r) = 0, and Poisson's equation reduces to the familiar Laplace equation:
[math]\Delta\Phi(\mathbf{r}) = \nabla^2 \Phi(\mathbf{r}) = 0[/math]
Keep in mind that in the absence of an electric charge source, you need to specify a non-zero potential somewhere in your structure, for example, on a perfect electric conductor (PEC). Otherwise, you will get a trivial zero solution of the Laplace equation.
Once the electric scalar potential is computed, the electric field can easily be computed via the equation below:
[math] \mathbf{E(r)} = - \nabla \Phi(\mathbf{r})[/math]
The Solution of Poisson's Equation
The general form of Poisson's equation for a scalar quantity Ψ(r) can be expressed as:
[math]\Delta\Psi(\mathbf{r}) = \nabla^2 \Psi(\mathbf{r}) = -f(\mathbf{r}) [/math]
where f is a general arbitrary function of the position vector r. In the case of a unit point source, the above equation reduces to:
[math]\Delta\Psi(\mathbf{r}) = \nabla^2 \Psi(\mathbf{r}) = -\delta(\mathbf{r}) [/math]
where δ(r) is the three-dimensional Dirac delta function. The solution to the above equation is called the Green's function of the Poisson equation for a certain boundary value problem and is denoted by G(r|r′). Then, the solution to the general Poisson equation can be expressed in the terms of the Green's function as follows:
[math] \Psi\mathbf{(r)} = \int\int\int_V G(\mathbf{r|r^{\prime}}) f(\mathbf{r^{\prime}}) dv^{\prime} [/math]
Free-Space Electric Field and Scalar Potential
There are very few boundary value problems for which you can find closed-form analytical Green's functions. One of them is the electric scalar potential due to a charge distribution in the free space. The potential Green's function for a free-space medium is given by:
[math] G_{\Phi}(\mathbf{r|r^{\prime}}) = -\frac{1}{4\pi | \mathbf{r - r^{\prime}} | } [/math]
If the volume charge density is denoted by ρ(r), then the electric scalar potential is given by:
[math] \Phi\mathbf{(r)} = \frac{1}{4\pi\epsilon} \int\int\int_V \frac{\rho(\mathbf{r^{\prime}})}{ | \mathbf{r - r^{\prime}} | } dv^{\prime} [/math]
where V is the volume containing the charge distribution.
The electric field due to the charge distribution is then given by:
[math] \mathbf{E(r)} = - \nabla \Phi(\mathbf{r}) = \frac{1}{4\pi\epsilon} \int\int\int_V \frac{\mathbf{r - r^{\prime}} }{ | \mathbf{r - r^{\prime}} |^3 } \rho(\mathbf{r^{\prime}}) dv^{\prime} [/math]
Static Fields Arising from Steady-State Conduction Currents
In an Ohmic conductor, the current density is related to the electric field as follows:
[math] \mathbf{J(r)} = \sigma \mathbf{E(r)} = -\sigma \nabla \Phi(\mathbf{r}) [/math]
where σ is the electric conductivity. On the other hand, the continuity equation for a stationary current requires no charge buildup or decay inside a closed region. This means that
[math] \nabla . \mathbf{J(r)} = 0 [/math]
These above two equations lead to the Laplace equation inside an Ohmic conductor medium:
[math]\nabla^2 \Phi(\mathbf{r}) = 0[/math]
In addition, the boundary condition at a conductor-dielectric interface requires a vanishing normal derivative of the electric potential:
[math] \frac{\partial \Phi}{\partial n} = 0 [/math]
At the interface between two contiguous conductors, the normal component of the current density must be continuous.
[math] \hat{\mathbf{n}} . [ \mathbf{J_2(r)} - \mathbf{J_1(r)} ] = 0 [/math]
which can be written as:
[math] \sigma_1 \hat{\mathbf{n}} . \mathbf{E_1(r)} = \sigma_2 \hat{\mathbf{n}} . \mathbf{E_2(r)} [/math]
Magnetostatics Analysis
At very low frequencies, as ω→0 and k→0, the Helmholtz equation for the magnetic vector potential reduces to the vector Poisson equation subject to specified boundary conditions:
[math]\Delta \mathbf{A} (\mathbf{r}) = \nabla^2 \mathbf{A}(\mathbf{r}) = - \mu \mathbf{J}(\mathbf{r}) [/math]
where A(r) is the magnetic vector potential, J(r) is the volume current density, and μ = μr μ0 is the permeability of the medium. The magnetic Poisson equation is vectorial in nature and involves a system of three scalar differential equations corresponding to the three components of A(r).
The magnetic field boundary conditions at the interface between two material media are:
[math] \hat{\mathbf{n}} . [ \mathbf{B_2(r)} - \mathbf{B_1(r)} ] = 0 [/math]
[math] \hat{\mathbf{n}} \times [ \mathbf{H_2(r)} - \mathbf{H_1(r)} ] = \mathbf{J_s(r)} [/math]
where [math] \hat{\mathbf{n}} [/math] is the unit normal vector at the interface pointing from medium 1 towards medium 2, B(r) = μH(r) is the magnetic flux density, H(r) is the magnetic field vector, and Js is the surface current density at the interface.
Once the magnetic vector potential is computed, the magnetic field can easily be computed via the equation below:
[math] \mathbf{H(r)} = \frac{1}{\mu} \nabla \times \mathbf{A} (\mathbf{r}) [/math]
The relationship between the magnetic flux density and magnetic field vectors is rather different inside permeable materials that have a permanent intrinsic magnetization. Examples of such materials are ferromagnetic material that are used as permanent magnets. When a permeable material has a permanent magnetization, the following relationship holds:
[math] \mathbf{B(r)} = {\mu} \big[ \mathbf{H(r)} + \mathbf{M(r)} \big] [/math]
where M(r) is the magnetization vector. In the SI units system, the magnetic field H and magnetization M both have the same units of A/m. It can be shown that for magnetostatic analysis, the effect of the permanent magnetization can be modeled as an equivalent volume current source:
[math] \mathbf{J_{eq}(r)} = \nabla \times \mathbf{M(r)} [/math]
If the magnetization vector is uniform and constant inside the volume, then its curl is zero everywhere inside the volume except on its boundary surface. In that case, the permanent magnetization can be effectively modeled by an equivalent surface current density on the surface of the permanent magnetic object:
[math] \mathbf{J_{s,eq}(r)} = \mathbf{M(r)} \times \hat{\mathbf{n}} [/math]
where [math] \hat{\mathbf{n}} [/math] is the unit outward normal vector at the surface of the permanent magnet object. Note that the volume of the permanent magnet still acts as a permeable material with a relative permeability of μ in the magnetostatic analysis.
Free-Space Magnetic Field and Vector Potential
The magnetic vector potential stratifies the vectorial form of Poisson's equation. Therefore, the free-space Green's function for the magnetic vector potential has the same functional dependence as that of the scalar electric potential but in a dyadic form, which is given by:
[math] \mathbf{\overline{\overline{G}}_A}(\mathbf{r|r^{\prime}}) = -\frac{1}{4\pi | \mathbf{r - r^{\prime}} | } \mathbf{\overline{\overline{I}}} [/math]
where is [math] \mathbf{\overline{\overline{I}}} [/math] is the unit dyad.
If the volume current density is denoted by J(r), then the magnetic vector potential is given by:
[math] \mathbf{A(r)} = \frac{\mu}{4\pi} \int\int\int_V \frac{ \mathbf{J(r^{\prime})}}{ | \mathbf{r - r^{\prime}} | } dv^{\prime} [/math]
where V is the volume containing the current distribution.
The magnetic field due to the current distribution is then given by:
[math] \mathbf{H(r)} = \frac{1}{\mu} \nabla \times \mathbf{A} (\mathbf{r}) = \frac{1}{4\pi} \int\int\int_V \mathbf{J(r^{\prime})} \times \frac{ \mathbf{r - r^{\prime}} }{ | \mathbf{r - r^{\prime}} |^3 } dv^{\prime} [/math]
The Finite Difference Technique
The general form of Poisson's equation for any potential ψ can be expressed as:
[math] \frac{\partial^2\psi}{\partial x^2} + \frac{\partial^2\psi}{\partial y^2} + \frac{\partial^2\psi}{\partial z^2} = -f(\mathbf{r}) [/math]
When f(r) = 0, one obtains the well-known Laplace equation, which applies to source-free regions.
The second derivative of ψ with respect to the x coordinate can be approximated by the second-order difference:
[math] \frac{\partial^2\psi(\mathbf{r})}{\partial x^2} \approx \frac{\psi(x+\Delta x,y,z)-2\psi(x,y,z)+\psi(x-\Delta x,y,z)}{(\Delta x)^2} [/math]
Similar expressions can be written for the second derivative with respect to the y and z coordinates.
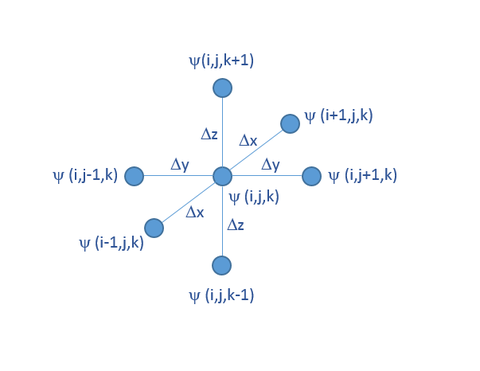
In the finite difference method, the computational domain is discretized using a 3D rectangular grid as shown on the figure below. The grid spacing along the three principal coordinate axes is denoted by Δx, Δy and Δz, respectively. In this grid, the coordinates of any point (x,y,z) in the space can be expressed as x = iΔx, y = jΔy and z = kΔz. Therefore, every point can simply be represented by an index triplet (i,j,k).
The potential at the point (x,y,z) can be expressed in terms of the potentials at its six neighboring grid points along the principal axes. This creates a 7-point computational molecule shown in the figure below:
In the special case of a uniform grid with Δx = Δy = Δz, it can be shown that in a source-free region:
[math] \psi(i,j,k) = \frac{1}{6} \big[ \psi(i+1,j,k) + \psi(i-1,j,k) + \psi(i,j+1,k) + \psi(i,j-1,k) + \psi(i,j,k+1) + \psi(i,j,k-1) \big] [/math]
Two types of domain boundary conditions can be applied:
- Dirichlet boundary condition: ψ = k =const.
- Neumann boundary condition: ∂ψ/∂n = k = const.
In the above, ∂ψ/∂n denotes the normal derivative of the potential at the surface of the domain boundary. EM.Ferma's default domain boundary condition for both the electrostatic and magnetostatic solvers is Dirichlet. At the interface between different material media, additional boundary conditions must be applied. These boundary conditions involve electric or magnetic field components. The field components can be expressed as partial derivatives of the potential, i.e. in the form of ∂ψ/∂x, ∂ψ/∂y or ∂ψ/∂z. Using the respective finite difference approximations of these derivatives, one arrives at fairly complicated difference equations involving the constitutive parameters ε, μ and σ, which must be solved simultaneously with the primary potential difference equations.
Note that the electrostatic Poisson and Laplace equations are of the scalar type, while the magnetostatic Poisson and Laplace equations are vectorial. As a result, the size of the numerical problem in the latter case is three times as large as the former case for the same mesh size.
2D Quasi-Static Solution of TEM Transmission Line Structures
At lower microwave frequencies (f < 10GHz), multi-conductor transmission line structures usually support either a dominant transverse electromagnetic (TEM) propagating mode or a dominant quasi-TEM propagating mode. These modes are almost non-dispersive, and their behavior can be regarded as frequency-independent. As a result, it is usually possible to perform a 2D electrostatic analysis of a transmission line structure and compute its characteristics impedance Z0 and effective permittivity εeff. The "quasi-static approach" to modeling of a TEM transmission line involves two steps:
- First, you have remove all the dielectric materials from your structure and replace them with free space (or air). Obtain a 2D electrostatic solution of your "air-filled" transmission line structure and compute its capacitance per unit length Ca.
- Next, obtain a 2D electrostatic solution of your actual transmission line structure with all of its dielectric parts and compute its true capacitance per unit length C.
Then effective permittivity of the transmission line structure is then calculated from the equation:
[math] \epsilon_{eff} = \frac{C}{C_a} [/math]
and its characteristic impedance is given by:
[math] Z_0 = \frac{\eta_0}{\sqrt{ \epsilon_{eff}}} = \eta_0 \sqrt{ \frac{C_a}{C} } [/math]
where η0 = 120π Ω is the intrinsic impedance of the free space.
The guide wavelength of your transmission line at a given frequency f is then calculated from:
[math] \lambda_g = \frac{\lambda_0}{\sqrt{\epsilon_{eff}}} = \frac{c}{f\sqrt{\epsilon_{eff}}} [/math]
and its propagation constant is given by:
[math] \beta = k_0\sqrt{\epsilon_{eff}} = \frac{2\pi f}{c}\sqrt{\epsilon_{eff}} [/math]
where c is the speed of light in the free space.