Difference between revisions of "EM.Ferma"
Kazem Sabet (Talk | contribs) (→Methods Of Electrostatics, Magnetostatics & Quasi-Statics) |
Kazem Sabet (Talk | contribs) (→Methods Of Electrostatics, Magnetostatics & Quasi-Statics) |
||
| Line 13: | Line 13: | ||
| − | The boundary conditions at the interface between two material media are: | + | The electric field boundary conditions at the interface between two material media are: |
| + | |||
| + | <math> \hat{\mathbf{n}} \dot [ \mathbf{D_2(r)} - \mathbf{D_1(r)} ] = \rho_s (\mathbf{r}) </math> | ||
| − | |||
<math> \hat{\mathbf{n}} \times [ \mathbf{E_2(r)} - \mathbf{E_1(r)} ] = 0 </math> | <math> \hat{\mathbf{n}} \times [ \mathbf{E_2(r)} - \mathbf{E_1(r)} ] = 0 </math> | ||
| + | |||
| + | |||
| + | where <b>D(r)</b> = ε<b>E(r)</b> is the electric flux density, <b>E(r)</b> is the electric field vector, and ρ<sub>s</sub> is the surface charge density at the interface. | ||
| Line 23: | Line 27: | ||
<math>\Delta\Phi(\mathbf{r}) = \nabla^2 \Phi(\mathbf{r}) = 0</math> | <math>\Delta\Phi(\mathbf{r}) = \nabla^2 \Phi(\mathbf{r}) = 0</math> | ||
| + | |||
| + | |||
| + | It must be noted that in the absence of an electric charge source, you need to specify a non-zero potential somewhere in your structure. Otherwise, you will get a trivial zero solution of the Laplace equation. | ||
| Line 36: | Line 43: | ||
where <b>A(r)</b> is the magnetic vector potential, <b>J(r)</b> is the volume current density, and μ is the permeability of the medium. The magnetic Poisson equation is vectorial in nature and involves a system of three scalar differential equations corresponding to the three components of <b>A(r)</b>. | where <b>A(r)</b> is the magnetic vector potential, <b>J(r)</b> is the volume current density, and μ is the permeability of the medium. The magnetic Poisson equation is vectorial in nature and involves a system of three scalar differential equations corresponding to the three components of <b>A(r)</b>. | ||
| + | |||
| + | |||
| + | The magnetic field boundary conditions at the interface between two material media are: | ||
| + | |||
| + | <math> \hat{\mathbf{n}} \dot [ \mathbf{B_2(r)} - \mathbf{B_1(r)} ] = 0 </math> | ||
| + | |||
| + | |||
| + | <math> \hat{\mathbf{n}} \times [ \mathbf{H_2(r)} - \mathbf{H_1(r)} ] = \mathbf{J_s(r)} </math> | ||
| + | |||
| + | |||
| + | where <b>B(r)</b> = μ<b>H(r)</b> is the magnetic flux density, <b>H(r)</b> is the magnetic field vector, and <b>J<sub>s</sub></b> is the surface current density at the interface. | ||
Revision as of 15:35, 26 May 2015
EM.Ferma is EM.CUBE's 3D static solver. It features two distinct electrostatic and magnetostatic simulation engines that can be used to solve a variety of static and low-frequency electromagnetic problems. Both simulation engines are based on finite difference solutions of Poisson's equation for electric and magnetic potentials.
With EM.Ferma, you can explore the electric fields due to volume charge distributions or fixed-potential perfect conductors, and magnetic fields due to wire or volume current sources and permanent magnets. Your structure may include dielectric or magnetic (permeable) material blocks. You can also use EM.Ferma's 2D quasi-static mode to compute the characteristic impedance (Z0) and effective permittivity of transmission line structures with complex cross section profiles.
Contents
Methods Of Electrostatics, Magnetostatics & Quasi-Statics
EM.Ferma solves the Poisson equation for the electric scalar potential subject to specified boundary conditions:
[math]\Delta\Phi(\mathbf{r}) = \nabla^2 \Phi(\mathbf{r}) = -\frac{\rho(\mathbf{r})}{\epsilon}[/math]
where Φ(r) is the electric scalar potential, ρ(r) is the volume charge density, and ε is the permittivity of the medium.
The electric field boundary conditions at the interface between two material media are:
[math] \hat{\mathbf{n}} \dot [ \mathbf{D_2(r)} - \mathbf{D_1(r)} ] = \rho_s (\mathbf{r}) [/math]
[math] \hat{\mathbf{n}} \times [ \mathbf{E_2(r)} - \mathbf{E_1(r)} ] = 0 [/math]
where D(r) = εE(r) is the electric flux density, E(r) is the electric field vector, and ρs is the surface charge density at the interface.
In a source-free region, ρ(r) = 0, and Poisson's equation reduces to the familiar Laplace equation:
[math]\Delta\Phi(\mathbf{r}) = \nabla^2 \Phi(\mathbf{r}) = 0[/math]
It must be noted that in the absence of an electric charge source, you need to specify a non-zero potential somewhere in your structure. Otherwise, you will get a trivial zero solution of the Laplace equation.
Once the electric scalar potential is computed, the electric field can easily be computed via the equation below:
[math] \mathbf{E(r)} = - \nabla \Phi(\mathbf{r})[/math]
EM.Ferma also solves the Poisson equation for the magnetic vector potential subject to specified boundary conditions:
[math]\Delta \mathbf{A} (\mathbf{r}) = \nabla^2 \mathbf{A}(\mathbf{r}) = - \mu \mathbf{J}(\mathbf{r}) [/math]
where A(r) is the magnetic vector potential, J(r) is the volume current density, and μ is the permeability of the medium. The magnetic Poisson equation is vectorial in nature and involves a system of three scalar differential equations corresponding to the three components of A(r).
The magnetic field boundary conditions at the interface between two material media are:
[math] \hat{\mathbf{n}} \dot [ \mathbf{B_2(r)} - \mathbf{B_1(r)} ] = 0 [/math]
[math] \hat{\mathbf{n}} \times [ \mathbf{H_2(r)} - \mathbf{H_1(r)} ] = \mathbf{J_s(r)} [/math]
where B(r) = μH(r) is the magnetic flux density, H(r) is the magnetic field vector, and Js is the surface current density at the interface.
Once the magnetic vector potential is computed, the magnetic field can easily be computed via the equation below:
[math] \mathbf{H(r)} = \frac{1}{\mu} \nabla \times \mathbf{A} (\mathbf{r})[/math]
Sources in EM.Ferma
For static analysis, the model can be excited with any number of Voltage Sources, Charge Sources, or Current Sources. For Quasistatic analysis, only Voltage Sources are of practical use.
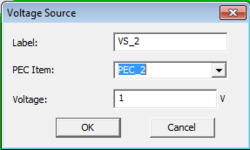
Voltage Sources
In EM.Ferma, Voltage Sources are applied to a specified PEC material group that exists in EM.CUBE's navigation tree. All CAD objects under the specified PEC group will act as Voltage Sources.
To add a new Voltage Source to a project, right-click on "Voltage Sources" on the navigation tree, and select "Insert Voltage Source...". In the Voltage Source dialog, select the PEC group to which the specified voltage will be applied. Enter any string as the Voltage -- a text string will be interpreted as a variable which can be used for parametric design, or a parameter sweep.
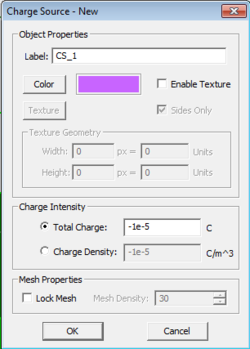
Charge Sources
Charge Sources in EM.Ferma apply a charge (or charge density) to a region defined by any of EM.CUBE's CAD objects.
Adding a new Charge Source is very similar to adding a new material in EM.CUBE. Find the "Charge Source" group label in the navigation tree and select "Insert New Charge Source..." A dialog will prompt the user to decide whether charge for this group will be defined in terms of total charge or charge density. If charge density is chosen, the specified charge density will be applied to all CAD objects defined in the present Charge Source group. If total charge is selected, the specified total charge will be distributed amongst the total volume of all objects under the present material group.
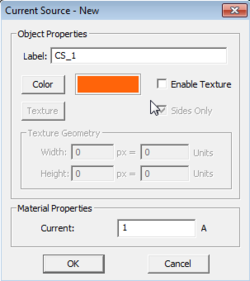
Current Sources
Current Sources in EM.Ferma apply a specified current to any number of one-dimensional CAD objects, such as Lines, Polylines, or Spirals. For any curve, such as a Parabola or a Circle, the user will be prompted to perform a one-time conversion to a Polyline just before running a simulation.
Adding a new Current Source is very similar to adding a new Charge Source. Keep in mind only one-dimensional objects can be drawn under this material group.
Observables in EM.Ferma
Field Sensor
Just like other EM.CUBE Modules, EM.Ferma has a standard Field Sensor observable. To specify a Field Sensor, right-click on "Field Sensors" in the navigation tree and click "Add New...". The Field Sensor dialog allows the user to select the direction of the sensor, visualization type, and whether E-field output or H-field output will be shown during a sweep analysis.
In EM.Ferma, Field Sensors are also used to specify 2D solution planes for EM.Ferma's 2D solution mode. This will be detailed shortly.
The E-fields and H-fields are computed at each mesh node within the specified 2D Field Sensor plane. In other words, the resolution of the Field Sensor is controlled by the mesh resolution.
Transmission Line Characteristics
In EM.Ferma's quasistatic mode, transmission-line parameters Z0 and EpsEff are computed, in addition to output due to the Field Sensor, which is required to define the 2D solution plane. Text files corresponding to these observables will be placed in the project's working directory after each analysis.
Domain and Boundary Conditions
In EM.Ferma, the Laplace equation is solved subject to boundary conditions. Here, we will discuss how to specify these boundary conditions.
3D Domain
EM.Ferma's computational domain defines where the boundary condition will be specified. The domain can be seen as a green cubic wireframe that surrounds all of the CAD objects in the model. To modify the domain boundary, find the "3D Static Domain" entry in the navigation tree, right-click on it, and select "Domain Settings...". The domain dialog will appear. In the domain dialog, the domain boundary can be specified in terms of either a custom, fixed location, or as custom offsets from CAD objects in the scene.
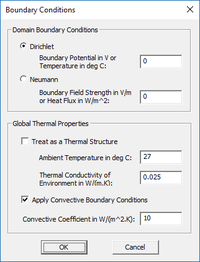
Boundary Condition
EM.Ferma allows the user to either specify the potential on the boundary (Dirichlet boundary condition), or specify the normal derivative on the boundary (Neumann boundary condition) via a specified field strength. To modify the boundary condition, find "Boundary Conditions" on the navigation tree, and select "Boundary Conditions...". The user will be prompted with the dialog seen at right.
2D Solution Planes in EM.Ferma
EM.Ferma features a 2D solution mode where the model is treated as a longitudinally infinite structure at a list of specified 2D Solution Planes. The 2D planes are defined by a Field Sensor definition that already exists in the project.
To explore EM.Ferma's 2D mode, right-click on "2D Solution Planes" in the navigation tree and select "2D Domain Settings...". In the 2D Static Domain dialog, enable the checkbox labeled "Treat Structure as Longitudinally Infinite across Each 2D Plane Specified Below". The user is then able to Add or Edit 2D Solution Plane definitions to the solution list.
Setting up a Transmission Line Simulation
To perform a Transmission Line simulation, first turn on Quasistatic simulation mode for a selected 2D Solution Plane, as shown in the figure at right. If an analysis is run with this option checked, the characteristic impedance (Z0) and Effective Epsilon will be computed for the corresponding 2D Solution Plane. This output can be found in appropriately-named text files in the project directory upon completion of the simulation. Fields and potentials at the selected 2D plane will still be computed. Many 2D quasistatic solutions can be obtained in the same analysis, if for example, your design contains many types of transmission lines.
Quasistatic analysis can only be performed with a Dirichlet boundary condition with 0V specified on the boundaries.
For a step-by-step demonstration (including transmission line optimization), take a look at this video on our YouTube channel: EM.CUBE Microstrip Optimization
Simulation Modes
EM.Ferma currently offers Analysis, Parametric Sweep, and Optimization simulation modes. More information about these simulation modes can be found on the Optimization page.
Simulation Examples / Gallery
Version History
- First available in EM.CUBE 14.2