Difference between revisions of "EM.Ferma"
Kazem Sabet (Talk | contribs) (→Modeling Transmission Lines Using EM.Ferma) |
(→Variety of Physical Objects in EM.Ferma) |
||
| (261 intermediate revisions by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | [[EM. | + | [[Image:Splash-static.jpg|right|720px]] |
| + | <strong><font color="#2603c4" size="4">Electrostatic, Magnetostatic & Thermal Solvers For DC And Low Frequency Simulations</font></strong> | ||
| + | <table> | ||
| + | <tr> | ||
| + | <td>[[image:Cube-icon.png | link=Getting_Started_with_EM.Cube]] [[image:cad-ico.png | link=Building_Geometrical_Constructions_in_CubeCAD]] [[image:fdtd-ico.png | link=EM.Tempo]] [[image:prop-ico.png | link=EM.Terrano]] [[image:planar-ico.png | link=EM.Picasso]] [[image:metal-ico.png | link=EM.Libera]] [[image:po-ico.png | link=EM.Illumina]]</td> | ||
| + | <tr> | ||
| + | </table> | ||
| + | [[Image:Tutorial_icon.png|30px]] '''[[EM.Cube#EM.Ferma_Documentation | EM.Ferma Tutorial Gateway]]''' | ||
| − | + | [[Image:Back_icon.png|30px]] '''[[EM.Cube | Back to EM.Cube Main Page]]''' | |
| + | ==Product Overview== | ||
| − | == | + | === EM.Ferma in a Nutshell === |
| − | + | EM.Ferma is a 3D static solver. It features two distinct electrostatic and magnetostatic simulation engines and a steady-state thermal simulation engine that can be used to solve a variety of static and low-frequency electromagnetic and thermal problems. The thermal solver includes both conduction and convection heat transfer mechanisms. All the three simulation engines are based on finite difference solutions of Poisson's equation for electric and magnetic potentials and temperature. | |
| − | EM.Ferma | + | With EM.Ferma, you can explore the electric fields due to volume charge distributions or fixed-potential perfect conductors, and magnetic fields due to wire or volume current sources and permanent magnets. Your structure may include dielectric or magnetic (permeable) material blocks. Using the thermal simulator, you can solve for the steady-state temperature distribution of structures that include perfect thermal conductors, insulators and volume heat sources. You can also use EM.Ferma's 2D quasi-static mode to compute the characteristic impedance (Z0) and effective permittivity of transmission line structures with complex cross section profiles. |
| − | + | [[Image:Info_icon.png|30px]] Click here to learn more about the '''[[Electrostatic & Magnetostatic Field Analysis | Theory of Electrostatic and Magnetostatic Methods]]'''. | |
| + | [[Image:Info_icon.png|30px]] Click here to learn more about the '''[[Steady-State_Thermal_Analysis | Theory of Steady-State Heat Transfer Methods]]'''. | ||
| − | + | <table> | |
| + | <tr> | ||
| + | <td> | ||
| + | [[Image:Magnet lines1.png|thumb|left|400px| Vector plot of magnetic field distribution in a cylindrical permanent magnet.]] | ||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | === EM.Ferma as the Static Module of EM.Cube === | ||
| − | + | EM.Ferma is the low-frequency '''Static Module''' of '''[[EM.Cube]]''', a comprehensive, integrated, modular electromagnetic modeling environment. EM.Ferma shares the visual interface, 3D parametric CAD modeler, data visualization tools, and many more utilities and features collectively known as [[Building_Geometrical_Constructions_in_CubeCAD | CubeCAD]] with all of [[EM.Cube]]'s other computational modules. | |
| − | + | [[Image:Info_icon.png|30px]] Click here to learn more about '''[[Getting_Started_with_EM.Cube | EM.Cube Modeling Environment]]'''. | |
| + | === Advantages & Limitations of EM.Ferma's Static Simulator === | ||
| − | + | EM.Ferma computes the electric and magnetic fields independent of each other based on electrostatic and magnetostatic approximations, respectively. As a result, any "electromagnetic" coupling effects or wave retardation effects are ignored in the simulation process. In exchange, static or quasi-static solutions are computationally much more efficient than the full-wave solutions of Maxwell's equations. Therefore, for low-frequency electromagnetic modeling problems or for simulation of sub-wavelength devices, EM.Ferma offers a faster alternative to [[EM.Cube]]'s full-wave modules like [[EM.Tempo]], [[EM.Picasso]] or [[EM.Libera]]. EM.Ferma currently provides a fixed-cell brick volume mesh generator. To model highly irregular geometries or curved objects, you may have to use very small cell sizes, which may lead to a large computational problem. | |
| + | <table> | ||
| + | <tr> | ||
| + | <td> | ||
| + | [[Image:Ferma L8 Fig title.png|thumb|left|400px| Vector plot of electric field distribution in a coplanar waveguide (CPW) transmission line.]] | ||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| − | + | == EM.Ferma Features at a Glance == | |
| − | + | ||
| + | === Physical Structure Definition === | ||
| − | + | <ul> | |
| + | <li> | ||
| + | Perfect electric conductor(PEC) solids and surfaces (Electrostatics)</li> | ||
| + | <li> | ||
| + | Dielectric objects (Electrostatics)</li> | ||
| + | <li> | ||
| + | Magnetic (permeable) objects (Magnetostatics)</li> | ||
| + | <li> | ||
| + | Perfect thermal conductor (PTC) solids and surfaces (Thermal)</li> | ||
| + | <li> | ||
| + | Insulator objects (Thermal)</li> | ||
| + | </ul> | ||
| − | + | === Sources === | |
| + | <ul> | ||
| + | <li> | ||
| + | Fixed-potential PEC for maintaining equi-potential metal objects (Electrostatics)</li> | ||
| + | <li> | ||
| + | Volume charge sources (Electrostatics)</li> | ||
| + | <li> | ||
| + | Volume current sources (Magnetostatics)</li> | ||
| + | <li> | ||
| + | Wire current sources (Magnetostatics)</li> | ||
| + | <li> | ||
| + | Permanent magnets (Magnetostatics)</li> | ||
| + | <li> | ||
| + | Fixed-temperature PTC for maintaining iso-thermal objects (Thermal)</li> | ||
| + | <li> | ||
| + | Volume heat sources (Thermal)</li> | ||
| + | </ul> | ||
| − | + | === Mesh generation === | |
| + | <ul> | ||
| + | <li> | ||
| + | Fixed-size brick cells</li> | ||
| + | </ul> | ||
| − | + | === 3D Electrostatic & Magnetostatic Simulation === | |
| − | < | + | <ul> |
| + | <li> | ||
| + | Finite difference solution of Laplace and Poisson equations for the electric scalar potential with Dirichlet and Neumann domain boundary conditions </li> | ||
| + | <li> | ||
| + | Finite difference solution of Laplace and Poisson equations for the magnetic vector potential with Dirichlet domain boundary conditions </li> | ||
| + | <li> | ||
| + | Calculation of electric scalar potential and electric field</li> | ||
| + | <li> | ||
| + | Calculation of magnetic vector potential and magnetic field</li> | ||
| + | <li> | ||
| + | Calculation of electric flux over user defined flux boxes and capacitance</li> | ||
| + | <li> | ||
| + | Calculation of magnetic flux over user defined flux surfaces and inductance</li> | ||
| + | <li> | ||
| + | Calculation of electric and magnetic energies, Ohmic power loss and resistance</li> | ||
| + | <li> | ||
| + | Parametric sweep with variable object properties or source parameters</li> | ||
| + | </ul> | ||
| + | === 2D Quasi-Static Simulation === | ||
| − | + | <ul> | |
| + | <li> | ||
| + | 2D Finite difference solution of cross section of transmission line structures</li> | ||
| + | <li> | ||
| + | 3D domain solution as well as 2D solution of a longitudinally infinite version of the structure defined on a 2D plane </li> | ||
| + | <li> | ||
| + | Calculation of electric potential and electric field distribution</li> | ||
| + | <li> | ||
| + | Parametric sweep of transmission line's geometric and material parameters</li> | ||
| + | <li> | ||
| + | Optimization of transmission line's parameters for impedance design</li> | ||
| + | </ul> | ||
| − | + | === Steady-State Thermal Simulation === | |
| − | < | + | <ul> |
| + | <li> | ||
| + | Finite difference solution of Laplace and Poisson equations for the temperature with Dirichlet and Neumann domain boundary conditions </li> | ||
| + | <li> | ||
| + | Calculation of temperature and heat flux density</li> | ||
| + | <li> | ||
| + | Calculation of thermal energy density on field sensor planes</li> | ||
| + | <li> | ||
| + | Calculation of thermal flux over user defined flux boxes</li> | ||
| + | <li> | ||
| + | Calculation of thermal energy</li> | ||
| + | </ul> | ||
| + | === Data Generation & Visualization === | ||
| − | + | <ul> | |
| + | <li> | ||
| + | Electric and magnetic field intensity and vector plots on planes</li> | ||
| + | <li> | ||
| + | Electric and magnetic potential intensity plots on planes</li> | ||
| + | <li> | ||
| + | Temperature and heat flux intensity and vector plots on planes</li> | ||
| + | <li> | ||
| + | Electric and magnetic energy density, dissipated power density and thermal energy density plots on planes</li> | ||
| + | <li> | ||
| + | Animation of field and potential plots after parametric sweeps</li> | ||
| + | <li> | ||
| + | Graphs of characteristic impedance and effective permittivity of transmission line structures vs. sweep variables</li> | ||
| + | <li> | ||
| + | Custom output parameters defined as mathematical expressions of standard outputs</li> | ||
| + | </ul> | ||
| + | == Building the Physical Structure in EM.Ferma == | ||
| − | + | === Variety of Physical Objects in EM.Ferma === | |
| − | + | The simplest static problems involve a charge source in the free space that produces an electric field, or a current source in the free space that produces a magnetic field. In such cases, the only applicable boundary conditions are defined at the boundary of the computational domain. As soon as you introduce a dielectric object next to a charge source or a magnetic (permeable) material next to a current source, you have to deal with a complex boundary value problem. In other words, you need to solve the electric or magnetic Poisson equation subject to the domain boundary conditions as well as material interface boundary conditions. The simplest thermal problem involves one or more thermal plates held at fixed temperatures. Once you introduce material blocks, you have to enforce conductive and convective boundary conditions at the interface between different materials and air. EM.Ferma uses the Finite Difference (FD) technique to find a numerical solution of your static boundary value problem. | |
| + | [[EM.Ferma]] offers the following types of physical objects: | ||
| − | + | {| class="wikitable" | |
| + | |- | ||
| + | ! scope="col"| Icon | ||
| + | ! scope="col"| Physical Object Type | ||
| + | ! scope="col"| Applications | ||
| + | ! scope="col"| Geometric Object Types Allowed | ||
| + | ! scope="col"| Notes & Restrictions | ||
| + | |- | ||
| + | | style="width:30px;" | [[File:pec_group_icon.png]] | ||
| + | | style="width:200px;" | [[Glossary of EM.Cube's Materials, Sources, Devices & Other Physical Object Types#Fixed-Potential PEC |Fixed-Potential Perfect Electric Conductor (PEC)]] | ||
| + | | style="width:300px;" | Modeling perfect metals with a fixed voltage | ||
| + | | style="width:100px;" | Solid and surface objects | ||
| + | | style="width:250px;" | Can be considered an electric source if the fixed voltage is nonzero | ||
| + | |- | ||
| + | | style="width:30px;" | [[File:diel_group_icon.png]] | ||
| + | | style="width:200px;" | [[Glossary of EM.Cube's Materials, Sources, Devices & Other Physical Object Types#Dielectric Material |Dielectric/Magnetic Material]] | ||
| + | | style="width:300px;" | Modeling any homogeneous or inhomogeneous material | ||
| + | | style="width:100px;" | Solid objects | ||
| + | | style="width:250px;" | non-source material | ||
| + | |- | ||
| + | | style="width:30px;" | [[File:aniso_group_icon.png]] | ||
| + | | style="width:200px;" | [[Glossary of EM.Cube's Materials, Sources, Devices & Other Physical Object Types#Volume Charge |Volume Charge]] | ||
| + | | style="width:300px;" | Modeling volume charge sources with a fixed charge density or an expression in the global coordinates (x,y,z) | ||
| + | | style="width:100px;" | Solid objects | ||
| + | | style="width:250px;" | Acts as an electric source | ||
| + | |- | ||
| + | | style="width:30px;" | [[File:voxel_group_icon.png]] | ||
| + | | style="width:200px;" | [[Glossary of EM.Cube's Materials, Sources, Devices & Other Physical Object Types#Volume Current |Volume Current]] | ||
| + | | style="width:300px;" | Modeling volume current sources with a fixed volume current density vector or expressions in the global coordinates (x,y,z) | ||
| + | | style="width:100px;" | Solid objects | ||
| + | | style="width:250px;" | Acts as a magnetic source | ||
| + | |- | ||
| + | | style="width:30px;" | [[File:pmc_group_icon.png]] | ||
| + | | style="width:200px;" | [[Glossary of EM.Cube's Materials, Sources, Devices & Other Physical Object Types#Permanent Magnet |Permanent Magnet]] | ||
| + | | style="width:300px;" | Modeling permanent magnet sources with a fixed magnetization vector or expressions in the global coordinates (x,y,z) | ||
| + | | style="width:100px;" | Solid objects | ||
| + | | style="width:250px;" | Acts as a magnetic source | ||
| + | |- | ||
| + | | style="width:30px;" | [[File:thin_group_icon.png]] | ||
| + | | style="width:200px;" | [[Glossary of EM.Cube's Materials, Sources, Devices & Other Physical Object Types#Wire Current |Wire Current]] | ||
| + | | style="width:300px;" | Modeling wire current sources | ||
| + | | style="width:100px;" | Line and polyline objects | ||
| + | | style="width:250px;" | Acts as a magnetic source | ||
| + | |- | ||
| + | | style="width:30px;" | [[File:pec_group_icon.png]] | ||
| + | | style="width:200px;" | [[Glossary of EM.Cube's Materials, Sources, Devices & Other Physical Object Types#Fixed-Temperature PTC |Fixed-Temperature Perfect Thermal Conductor (PTC)]] | ||
| + | | style="width:300px;" | Modeling isothermal surfaces with a fixed temperature | ||
| + | | style="width:100px;" | Solid and surface objects | ||
| + | | style="width:250px;" | Can be considered a thermal source if the fixed temperature is different than the ambient temperature (shares the same navigation tree node as PEC object) | ||
| + | |- | ||
| + | | style="width:30px;" | [[File:diel_group_icon.png]] | ||
| + | | style="width:200px;" | [[Glossary of EM.Cube's Materials, Sources, Devices & Other Physical Object Types#Dielectric Material |Insulator Material]] | ||
| + | | style="width:300px;" | Modeling any homogeneous or inhomogeneous material | ||
| + | | style="width:100px;" | Solid objects | ||
| + | | style="width:250px;" | non-source material (shares the same navigation tree node as dielectric material) | ||
| + | |- | ||
| + | | style="width:30px;" | [[File:aniso_group_icon.png]] | ||
| + | | style="width:200px;" | [[Glossary of EM.Cube's Materials, Sources, Devices & Other Physical Object Types#Volume Heat Source |Volume Heat Source]] | ||
| + | | style="width:300px;" | Modeling volume heat sources with a fixed heat density or an expression in the global coordinates (x,y,z) | ||
| + | | style="width:100px;" | Solid objects | ||
| + | | style="width:250px;" | Acts as a thermal source (shares the same navigation tree node as volume charge) | ||
| + | |- | ||
| + | | style="width:30px;" | [[File:Virt_group_icon.png]] | ||
| + | | style="width:200px;" | [[Glossary of EM.Cube's Materials, Sources, Devices & Other Physical Object Types#Virtual_Object_Group | Virtual Object]] | ||
| + | | style="width:300px;" | Used for representing non-physical items | ||
| + | | style="width:100px;" | All types of objects | ||
| + | | style="width:250px;" | None | ||
| + | |} | ||
| + | Click on each category to learn more details about it in the [[Glossary of EM.Cube's Materials, Sources, Devices & Other Physical Object Types]]. | ||
| − | + | === Grouping Objects by Material or Source Type === | |
| − | + | ||
| + | Your physical structure in EM.Ferma is typically made up of some kind of source object either in the free space or in the presence of one or more material objects. EM.Ferma's electrostatic and magnetostatic or thermal simulation engines then discretize the entire computational domain including these source and material objects and solve the Laplace or Poisson equations to find the electric or magnetic fields or temperature everywhere in the computational domain. | ||
| − | + | All the geometric objects in the project workspace are organized together into object groups which share the same properties including color and electric or magnetic parameters. It is recommended that you first create object groups, and then draw new objects under the active group. To create a new object group, right-click on its category name in the "Physical Structure" section of the navigation tree and select one of the "Insert New Group..." items from the contextual menu. However, if you start a new EM.Ferma project from scratch, and start drawing a new object without having previously defined any object groups, a new default "Fixed-Potential PEC" object group with a zero voltage is created and added to the navigation tree to hold your new geometric object. | |
| − | + | It is important to note that there is a one-to-one correspondence between electrostatic and thermal simulation entities: | |
| − | == | + | {| class="wikitable" |
| + | |- | ||
| + | ! scope="col"| Electrostatic Item | ||
| + | ! scope="col"| Corresponding Thermal Item | ||
| + | |- | ||
| + | | style="width:200px;" | Electric Scalar Potential | ||
| + | | style="width:200px;" | Temperature | ||
| + | |- | ||
| + | | style="width:200px;" | Electric Field | ||
| + | | style="width:200px;" | Heat Flux Density | ||
| + | |- | ||
| + | | style="width:200px;" | Perfect Electric Conductor | ||
| + | | style="width:200px;" | Perfect Thermal Conductor | ||
| + | |- | ||
| + | | style="width:200px;" | Dielectric Material | ||
| + | | style="width:200px;" | Insulator Material | ||
| + | |- | ||
| + | | style="width:200px;" | Volume Charge | ||
| + | | style="width:200px;" | Volume Heat Source | ||
| + | |} | ||
| − | + | {{Note|Electrostatic and thermal solvers share the same material categories on the navigation tree. This means that PEC objects are treated as PTC objects, dielectric objects are treated as insulator objects and volume charges are treated as volume heat sources when the thermal solver is enabled.}} | |
| − | + | Once a new object group node has been created in the navigation tree, it becomes and remains the "Active" object group, which is always listed in bold letters. When you draw a new geometric object such as a box or a sphere, its name is added under the currently active object group. There is only one object group that is active at any time. Any group can be made active by right-clicking on its name in the navigation tree and selecting the '''Activate''' item of the contextual menu. | |
| − | + | [[Image:Info_icon.png|30px]] Click here to learn more about '''[[Building Geometrical Constructions in CubeCAD#Transferring Objects Among Different Groups or Modules | Moving Objects among Different Groups]]'''. | |
| − | + | <table> | |
| + | <tr> | ||
| + | <td> [[Image:STAT MAN1.png|thumb|left|480px|EM.Ferma's navigation tree.]] </td> | ||
| + | </tr> | ||
| + | </table> | ||
| − | === | + | === A Note on Material and Source Types in EM.Ferma === |
| − | + | In [[EM.Cube]]'s other modules, material types are categorized under the "Physical Structure" section of the navigation tree, and sources are organized under a separate "Sources" section. In those modules, all the geometric objects you draw in your project workspace typically represent material bodies. All of [[EM.Cube]] modules except for EM.Ferma require at least one excitation source to be selected from the "Sources" section of the navigation tree before you can run a simulation. | |
| − | + | In EM.Ferma, materials and sources are all lumped together and listed under the "Physical Structure" section of the navigation tree. In other words, there is no separate "Sources" section. For example, you can define default zero-potential perfect electric conductors (PEC) in your project to model metal objects. You can also define fixed-potential PEC objects with a nonzero voltage, which can effectively act as a voltage source for your boundary value problem. In this case, you will solve the Lapalce equation subject to the specified nonzero potential boundary values. Both types of PEC objects are defined from the same PEC node of the navigation tree by assigning different voltage values. Charge and current sources are also defined as geometric objects, and you have to draw them in the project workspace just like other material objects. | |
| − | + | == EM.Ferma's Computational Domain == | |
| − | === | + | ===The Domain Box=== |
| − | + | In EM.Ferma, the Poisson or Laplace equations are solved subject to boundary conditions using the Finite Difference technique. As a result, you need to specify a finite computational domain and then specify the domain boundary conditions. EM.Ferma's computational domain defines where the domain boundary condition will be specified. A default domain box is always placed in the project workspace as soon as you draw your first object. The domain can be seen as a blue cubic wireframe that surrounds all of the CAD objects in the project workspace. | |
| − | To | + | To modify the domain settings, click the Domain button of the Simulate Toolbar or right-click on "3D Static Domain" entry in the Navigation Tree and select "Domain Settings..." from the contextual menu. In the Domain Settings Dialog, the computational domain can be defined in two different ways: Default and Custom. The default type places an enclosing box with a specified offset from the largest bounding box of your project's CAD objects. The default offset value is 20 project units, but you can change this value arbitrarily. The custom type defines a fixed domain box by specifying the coordinates of its two opposite corners labeled Min and Max in the world coordinate system. |
| − | + | <table> | |
| + | <tr> | ||
| + | <td> [[Image:Qsource5.png|thumb|left|480px|EM.Ferma's Domain Settings dialog.]] </td> | ||
| + | </tr> | ||
| + | </table> | ||
| − | === | + | ===Domain Boundary Conditions=== |
| − | + | *EM.Ferma allows you to specify the electric potential boundary conditions on the domain box. Two options are available. The Dirichlet boundary condition is the default option and is specified as a fixed potential value on the surface of the domain walls. By default, this value is 0 Volts. The Neumann boundary condition specifies the normal derivative of the electric scalar potential on the surface of the domain walls. This is equivalent to a constant normal electric field component on the domain walls and its value is specified in V/m. | |
| − | + | ||
| − | + | *The magnetostatic simulation engine always assumes Dirichlet domain boundary conditions and sets the values of the magnetic vector potential to zero on all the domain walls. | |
| − | + | *EM.Ferma provides two options for thermal boundary conditions on the domain box. The Dirichlet boundary condition is the default option and is specified as a fixed temperature value on the surface of the domain walls. By default, this value is 0°C. The Neumann boundary condition specifies the normal derivative of the temperature on the surface of the domain walls. This is equivalent to a constant heat flux passing through the domain walls and its value is specified in W/m<sup>2</sup>. A zero heat flux means a perfectly insulated domain box and is known as the adiabatic boundary condition. | |
| − | To | + | To modify the boundary conditions, right-click on "Boundary Conditions" in the navigation tree, and select "Boundary Conditions..." from the contextual menu to open the Boundary Conditions Dialog. When you switch from the electrostatic-magnetostatic solver to the thermal solver in EM.Ferma's Run Simulation dialog, it automatically checks the box labeled '''Treat as a Thermal Structure''' in the Boundary Conditions dialog. Conversely, if you check this box in the Boundary Conditions dialog, the solver type is set to the thermal solver in the Simulation Run dialog. In the "Global Thermal Properties" section of the Boundary Conditions dialog, you can set the values of the ambient temperature in °C, thermal conductivity of the environment in W/(m.K) and the convective coefficient in W/(m<sup>2</sup>.K). You can also disable the enforcement of the convective boundary condition on the surface of solid insulator objects. |
| − | + | <table> | |
| + | <tr> | ||
| + | <td> [[Image:fermbc.png|thumb|left|480px|EM.Ferma's Boundary Conditions dialog.]] </td> | ||
| + | </tr> | ||
| + | </table> | ||
| − | EM.Ferma | + | == EM.Ferma's Simulation Data & Observables == |
| − | + | At the end of an electrostatic simulation, the electric field vector and electric scalar potential values are computed at all the mesh grid points of the entire computational domain. At the end of an magnetostatic simulation, the magnetic field vector and magnetic vector potential values are computed at all the grid nodes. At the end of a thermal simulation, the temperature and heat flux vector are computed at all the mesh grid points of the entire computational domain. | |
| − | + | Besides the electric and magnetic fields and temperature, EM.Ferma can compute a number of field integral quantities such as voltage, current, flux, energy, etc. The field components, potential values and field integrals are written into output data files and can be visualized on the screen or graphed in Data Manager only if you define a field sensor or a field integral observable. In the absence of any observable defined in the navigation tree, the static simulation will be carried out and completed, but no output simulation data will be generated. | |
| − | + | EM.Ferma offers the following types of output simulation data: | |
| − | + | {| class="wikitable" | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | {| | + | |
|- | |- | ||
| − | + | ! scope="col"| Icon | |
| − | + | ! scope="col"| Simulation Data Type | |
| − | + | ! scope="col"| Observable Type | |
| − | + | ! scope="col"| Applications | |
| − | + | ||
| − | + | ||
|- | |- | ||
| + | | style="width:30px;" | [[File:fieldsensor_icon.png]] | ||
| + | | style="width:150px;" | Near-Field Distribution Maps | ||
| + | | style="width:150px;" | [[Glossary of EM.Cube's Simulation Observables & Graph Types#Near-Field_Sensor_Observable |Near-Field Sensor]] | ||
| + | | style="width:450px;" | Computing electric and magnetic field components, electric scalar potential and magnitude of magnetic vector potential on a planar cross section of the computational domain | ||
| + | |- | ||
| + | | style="width:30px;" | [[File:fieldsensor_icon.png]] | ||
| + | | style="width:150px;" | Electric and Magnetic Energy and Dissipated Power Density Maps | ||
| + | | style="width:150px;" | [[Glossary of EM.Cube's Simulation Observables & Graph Types#Near-Field_Sensor_Observable |Near-Field Sensor]] | ||
| + | | style="width:450px;" | Computing electric and magnetic energy densities and dissipated power density on a planar cross section of the computational domain | ||
| + | |- | ||
| + | | style="width:30px;" | [[File:fieldsensor_icon.png]] | ||
| + | | style="width:150px;" | Temperature and Heat Flux Distribution Maps | ||
| + | | style="width:150px;" | [[Glossary of EM.Cube's Simulation Observables & Graph Types#Near-Field_Sensor_Observable |Near-Field Sensor]] | ||
| + | | style="width:450px;" | Computing temperature and heat flux components on a planar cross section of the computational domain | ||
| + | |- | ||
| + | | style="width:30px;" | [[File:fieldsensor_icon.png]] | ||
| + | | style="width:150px;" | Thermal Energy Density Maps | ||
| + | | style="width:150px;" | [[Glossary of EM.Cube's Simulation Observables & Graph Types#Near-Field_Sensor_Observable |Near-Field Sensor]] | ||
| + | | style="width:450px;" | Computing thermal energy density on a planar cross section of the computational domain | ||
| + | |- | ||
| + | | style="width:30px;" | [[File:field_integ_icon.png]] | ||
| + | | style="width:150px;" | Field Integral Quantities | ||
| + | | style="width:150px;" | [[Glossary of EM.Cube's Simulation Observables & Graph Types#Static_Field_Integral_Observable | Static Field Integral]] | ||
| + | | style="width:450px;" | Computing line, surface and volume integrals of the electric and magnetic fields and heat flux | ||
|} | |} | ||
| + | Click on each category to learn more details about it in the [[Glossary of EM.Cube's Simulation Observables & Graph Types]]. | ||
| − | + | <table> | |
| − | + | <tr> | |
| − | [[Image: | + | <td> [[Image:Ferma L1 Fig15.png|thumb|left|640px|Electric field distribution of a spherical charge on a horizontal field sensor plane.]] </td> |
| − | + | </tr> | |
| − | + | <tr> | |
| − | + | <td> [[Image:Ferma L1 Fig16.png|thumb|left|640px|Electric scalar potential distribution of a spherical charge on a horizontal field sensor plane.]] </td> | |
| − | + | </tr> | |
| − | + | </table> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | The table below list the different types of field integrals and their definitions: | |
{| class="wikitable" | {| class="wikitable" | ||
|- | |- | ||
| − | |||
! scope="col"| Field Integral | ! scope="col"| Field Integral | ||
| + | ! scope="col"| Definition | ||
| + | ! scope="col"| Output Data File | ||
|- | |- | ||
! scope="row"| Voltage | ! scope="row"| Voltage | ||
| − | | <math> V = \int_C \mathbf{E(r)} . \mathbf{dl} </math> | + | | <math> V = - \int_C \mathbf{E(r)} . \mathbf{dl} </math> |
| + | | voltage.DAT | ||
|- | |- | ||
! scope="row"| Current | ! scope="row"| Current | ||
| − | | <math> I = \ | + | | <math> I = \oint_{C_o} \mathbf{H(r)} . \mathbf{dl} </math> |
| + | | current.DAT | ||
| + | |- | ||
| + | ! scope="row"| Conduction Current | ||
| + | | <math> I_{cond} = \int\int_S \mathbf{J(r)} . \mathbf{ds} = \int\int_S \sigma \mathbf{E(r)} . \mathbf{ds} </math> | ||
| + | | conduction_current.DAT | ||
|- | |- | ||
! scope="row"| Electric Flux | ! scope="row"| Electric Flux | ||
| <math> \Phi_E = \int\int_{S_o} \mathbf{D(r)} . \mathbf{ds} = \int\int_{S_o} \epsilon \mathbf{E(r)} . \mathbf{ds} </math> | | <math> \Phi_E = \int\int_{S_o} \mathbf{D(r)} . \mathbf{ds} = \int\int_{S_o} \epsilon \mathbf{E(r)} . \mathbf{ds} </math> | ||
| + | | flux_E.DAT | ||
|- | |- | ||
! scope="row"| Magnetic Flux | ! scope="row"| Magnetic Flux | ||
| <math> \Phi_H = \int\int_S \mathbf{B(r)} . \mathbf{ds} = \int\int_S \mu \mathbf{H(r)} . \mathbf{ds} </math> | | <math> \Phi_H = \int\int_S \mathbf{B(r)} . \mathbf{ds} = \int\int_S \mu \mathbf{H(r)} . \mathbf{ds} </math> | ||
| + | | flux_H.DAT | ||
|- | |- | ||
! scope="row"| Electric Energy | ! scope="row"| Electric Energy | ||
| − | | <math> W_E = \int \int \int_V \epsilon \vert \mathbf{E(r)} \vert ^2 dv </math> | + | | <math> W_E = \frac{1}{2} \int \int \int_V \epsilon \vert \mathbf{E(r)} \vert ^2 dv </math> |
| + | | energy_E.DAT | ||
|- | |- | ||
! scope="row"| Magnetic Energy | ! scope="row"| Magnetic Energy | ||
| − | | <math> W_H = \int\int\int_V \mu \vert \mathbf{H(r)} \vert ^2 dv </math> | + | | <math> W_H = \frac{1}{2} \int\int\int_V \mu \vert \mathbf{H(r)} \vert ^2 dv </math> |
| + | | energy_H.DAT | ||
| + | |- | ||
| + | ! scope="row"| Ohmic Power Loss | ||
| + | | <math> P_{ohmic} = \int\int\int_V \sigma \vert \mathbf{E(r)} \vert ^2 dv </math> | ||
| + | | ohmic.DAT | ||
|- | |- | ||
! scope="row"| Capacitance | ! scope="row"| Capacitance | ||
| − | | <math> C = | + | | <math> C = \Phi_E/V = \int\int_{S_o} \epsilon \mathbf{E(r)} . \mathbf{ds} / \int_C \mathbf{E(r)} . \mathbf{dl} </math> |
| + | | capacitance.DAT | ||
|- | |- | ||
| − | ! scope="row"| | + | ! scope="row"| Capacitance (Alternative) |
| − | | <math> | + | | <math> C = 2W_E/V^2 = 2 \int \int \int_V \epsilon \vert \mathbf{E(r)} \vert ^2 dv / \left( \int_C \mathbf{E(r)} . \mathbf{dl} \right)^2</math> |
| − | | | + | | capacitance.DAT |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|- | |- | ||
| − | ! scope=" | + | ! scope="row"| Self-Inductance |
| − | + | | <math> L = \Phi_H/I = \int\int_S \mu \mathbf{H(r)} . \mathbf{ds} / \oint_{C_o} \mathbf{H(r)} . \mathbf{dl} </math> | |
| + | | inductance.DAT | ||
|- | |- | ||
| − | ! scope="row"| | + | ! scope="row"| Self-Inductance (Alternative) |
| − | | | + | | <math> L = 2W_M/I^2 = 2 \int \int \int_V \mu \vert \mathbf{H(r)} \vert ^2 dv / \left( \oint_{C_o} \mathbf{H(r)} . \mathbf{dl} \right)^2</math> |
| + | | inductance.DAT | ||
|- | |- | ||
| − | ! scope="row"| | + | ! scope="row"| Mutual Inductance |
| − | | | + | | <math> M = \Phi_H^{\prime}/I = \int\int_{S^{\prime}} \mu \mathbf{H(r)} . \mathbf{ds} / \oint_{C_o} \mathbf{H(r)} . \mathbf{dl} </math> |
| + | | mutual_inductance.DAT | ||
|- | |- | ||
| − | ! scope="row"| | + | ! scope="row"| Resistance |
| − | | | + | | <math> R = V/I_{cond} = - \int_C \mathbf{E(r)} . \mathbf{dl} / \int\int_S \sigma \mathbf{E(r)} . \mathbf{ds} </math> |
| + | | resistance.DAT | ||
|- | |- | ||
| − | ! scope="row"| | + | ! scope="row"| Resistance (Alternative 1) |
| − | | | + | | <math> R = V^2/P_{ohmic} = \left( \int_C \mathbf{E(r)} . \mathbf{dl} \right)^2 / \int\int\int_V \sigma \vert \mathbf{E(r)} \vert ^2 dv </math> |
| + | | resistance.DAT | ||
|- | |- | ||
| − | ! scope="row"| | + | ! scope="row"| Resistance (Alternative 2) |
| − | | | + | | <math> R = P_{ohmic}/I_{cond}^2 = \int\int\int_V \sigma \vert \mathbf{E(r)} \vert ^2 dv / \left( \int\int_S \sigma \mathbf{E(r)} . \mathbf{ds} \right)^2</math> |
| + | | resistance.DAT | ||
| + | |- | ||
| + | ! scope="row"| Thermal Flux | ||
| + | | <math> \Phi_T = \int\int_{S_o} \mathbf{q(r)} . \mathbf{ds} </math> | ||
| + | | flux_T.DAT | ||
| + | |- | ||
| + | ! scope="row"| Thermal Energy | ||
| + | | <math> W_T = Q = \int \int \int_V \rho_V c_p \left( T\mathbf{(r)} - T_{env} \right) dv </math> | ||
| + | | energy_T.DAT | ||
|} | |} | ||
| + | <table> | ||
| + | <tr> | ||
| + | <td> | ||
| + | [[Image:Qsource13.png|thumb|left|480px|Defining the capacitance observable in the field integral dialog.]] | ||
| + | </td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <tr> | ||
| + | <td> | ||
| + | [[Image:Qsource11.png|thumb|left|480px|The electric flux box for calculation of charge around a capacitor.]] | ||
| + | </td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td> | ||
| + | [[Image:Qsource12.png|thumb|left|480px|A line defining the voltage path for calculation of voltage between capacitor plates.]] | ||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| − | + | == Discretizing the Physical Structure in EM.Ferma == | |
| − | + | ===The Static Mesh=== | |
| − | + | The Finite Difference technique discretizes the computational domain using a 3D rectangular grid. EM.Ferma generates a fixed-cell mesh. This means that the extents of the mesh cells along the principal axes are fixed: Δx, Δy, Δz. By default, the mesh cell size is set to one unit project along all the three directions (with Δx = Δy = Δz). To modify the cell size, click the Mesh Settings button of the Simulate Toolbar or right-click on "Static Mesh" in the Navigation Tree, and select "Mesh Settings..." from the contextual menu to open the Mesh Settings Dialog. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | To | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | {{Note|To obtain accurate results, it is highly recommended to use a square mesh as much as possible.}} | ||
| − | + | [[Image:Info_icon.png|30px]] Click here to learn more about '''[[Preparing_Physical_Structures_for_Electromagnetic_Simulation#Working_with_EM.Cube.27s_Mesh_Generators | Working with Mesh Generator]]'''. | |
| + | [[Image:Info_icon.png|30px]] Click here to learn more about the properties of '''[[Glossary_of_EM.Cube%27s_Simulation-Related_Operations#Fixed-Cell_Brick_Mesh | EM.Ferma's Fixed-Cell Brick Mesh Generator]]'''. | ||
| − | + | <table> | |
| + | <tr> | ||
| + | <td> [[Image:Qsource4.png|thumb|350px|EM.Ferma's Mesh Settings dialog.]] </td> | ||
| + | </tr> | ||
| + | </table> | ||
| − | + | <table> | |
| − | < | + | <tr> |
| + | <td> [[Image:Qsource2.png|thumb|360px|Geometry of a spherical charge source and the enclosing domain box.]] </td> | ||
| + | <td> [[Image:Qsource3.png|thumb|360px|Fixed-cel mesh of the spherical charge object.]] </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | == Running Static Simulations in EM.Ferma == | ||
| − | + | === EM.Ferma's Simulation Modes === | |
| + | [[EM.Ferma]] currently offers three different simulation modes as follows: | ||
| − | + | {| class="wikitable" | |
| + | |- | ||
| + | ! scope="col"| Simulation Mode | ||
| + | ! scope="col"| Usage | ||
| + | ! scope="col"| Number of Engine Runs | ||
| + | ! scope="col"| Frequency | ||
| + | ! scope="col"| Restrictions | ||
| + | |- | ||
| + | | style="width:120px;" | [[#Running an Electrostatic or Magnetostatic Analysis | Analysis]] | ||
| + | | style="width:270px;" | Simulates the physical structure "As Is" | ||
| + | | style="width:100px;" | Single run | ||
| + | | style="width:200px;" | N/A | ||
| + | | style="width:150px;" | None | ||
| + | |- | ||
| + | | style="width:120px;" | [[Parametric_Modeling_%26_Simulation_Modes_in_EM.Cube#Running_Parametric_Sweep_Simulations_in_EM.Cube | Parametric Sweep]] | ||
| + | | style="width:270px;" | Varies the value(s) of one or more project variables | ||
| + | | style="width:100px;" | Multiple runs | ||
| + | | style="width:200px;" | N/A | ||
| + | | style="width:150px;" | None | ||
| + | |- | ||
| + | | style="width:120px;" | [[Parametric_Modeling_%26_Simulation_Modes_in_EM.Cube#Performing_Optimization_in_EM.Cube | Optimization]] | ||
| + | | style="width:270px;" | Optimizes the value(s) of one or more project variables to achieve a design goal | ||
| + | | style="width:100px;" | Multiple runs | ||
| + | | style="width:200px;" | N/A | ||
| + | | style="width:150px;" | None | ||
| + | |} | ||
| − | + | === Running an Electrostatic, Magnetostatic or Thermal Analysis === | |
| + | [[EM.Ferma]] has three independent but functionally similar static simulation engines: Electrostatic, Magnetostatic and Thermal. The electrostatic engine solves the electric form of Poisson's equation for electric scalar potential subject to electric field boundary conditions, in the presence of electric sources (volume charges and fixed-potential PEC blocks) and dielectric material media. The magnetostatic engine solves the magnetic form of Poisson's equation for magnetic vector potential subject to magnetic field boundary conditions, in the presence of magnetic sources (wire and volume currents and permanent magnetic blocks) and magnetic material media. The thermal engine solves the thermal form of Poisson's equation for steady-state temperature subject to thermal boundary conditions, in the presence of heat sources (volume sources and fixed-temperature PTC blocks) and insulator material media. | ||
| − | + | To run a static simulation, first you have to open the Run Dialog. This is done by clicking the "Run" button of the Simulate Toolbar, or by selecting the "Run" item of the Simulate Menu, or simply using the keyboard shortcut "Ctrl+R". There are two available options for the simulation engine: '''Electrostatic-Magnetostatic Solver''' and '''Steady-State Thermal Solver'''. Clicking the Run button of this dialog starts a static analysis. A separate window pops up which reports the progress of the current simulation. | |
| − | < | + | <table> |
| + | <tr> | ||
| + | <td> [[Image:Ferma L1 Fig11.png|thumb|left|600px|EM.Ferma's Simulation Run dialog.]] </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | In EM.Ferma you don't have to choose between the electrostatic or magnetostatic simulation engines. The program looks at the types of sources and material objects present in your project workspace and then it determines whether an electrostatic analysis or a magnetostatic analysis or possibly both should be performed. When there are only electric sources present, you will get nonzero electric fields and zero magnetic fields. When there are only magnetic sources present, you will get nonzero magnetic fields and zero electric fields. On the other hand, since the electrostatic and thermal solvers share the same navigation resources, you can run only one of the two engines at a time. By default, the electrostatic solver is enabled. | ||
| − | + | An "Analysis" is the simplest simulation mode of EM.Ferma. It is a single-shot finite difference solution of your static problem. The physical structure of your project workspace is first discretized using a fixed-cell mesh and the Poisson equation is solved numerically everywhere in the computational domain. The field and potential values at each mesh node are computed, and the specified observables are written into data files. The other available simulation modes, parametric sweep and optimization, involve multiple runs of the static solvers. | |
| + | ===Static Simulation Engine Settings=== | ||
| − | + | EM.Ferma offers two different types of linear system solver for solving the matrix equations that result from discretization of Poisson's equation: an iterative solver based on the stabilized Bi-Conjugate Gradient (BiCG) method and a Gauss-Seidel solver. The default solver type is BiCG. You can specify some numerical parameters related to the BiCG solver. To do that, you need to open the Simulation Engine Settings Dialog by clicking the "Settings" button located next to the "Select Engine" drop-down list. From this dialog you can set the maximum number of BiCG iterations, which has a default value of 10,000. You can also set a value for "Convergence Error". The default value for electrostatic analysis is 0.001. For magnetostatic analysis, the specified value of convergence error is reduced by a factor 1000 automatically. Therefore, the default convergence error in this case is 10<sup>-6</sup>. | |
| − | + | {{Note|The value of convergence error affect the accuracy of your simulation results. For most practical scenarios, the default values are adequate. You can reduce the convergence error for better accuracy at the expense of longer computation time.}} | |
| − | + | <table> | |
| + | <tr> | ||
| + | <td> | ||
| + | [[Image:Qsource7.png|thumb|left|480px|EM.Ferma's Static Engine Settings dialog.]] | ||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| + | == The 2D Quasi-Static Simulation Mode== | ||
| + | EM.Ferma's electrostatic simulation engine features a 2D solution mode where your physical model is treated as a longitudinally infinite structure in the direction normal to specified "2D Solution Plane". A 2D solution plane is defined based on a "Field Sensor" definition that already exists in your project. To explore EM.Ferma's 2D mode, right-click on '''2D Solution Planes''' in the "Computational Domain" section of the navigation tree and select '''2D Domain Settings...''' from the contextual menu. In the 2D Static Domain dialog, check the checkbox labeled "Reduce the 3D Domain to a 2D Solution Plane". The first field sensor observable in the navigation tree is used for the definition of the 2D solution plane. | ||
| + | At the end of a 2D electrostatic analysis, you can view the electric field and potential results on the field sensor plane. It is assumed that your structure is invariant along the direction normal to the 2D solution plane. Therefore, your computed field and potential profiles must be valid at all the planes perpendicular to the specified longitudinal direction. A 2D structure of this type can be considered to represent a transmission line of infinite length. EM.Ferma also performs a quasi-static analysis of the transmission line structure, and usually provides good results at lower microwave frequencies (f < 10GHz). It computes the characteristics impedance Z<sub>0</sub> and effective permittivity ε<sub>eff</sub> of the multi-conductor TEM or quasi-TEM transmission line. The results are written to two output data files named "solution_plane_Z0.DAT" and "solution_plane_EpsEff.DAT", respectively. | ||
| − | + | <table> | |
| + | <tr> | ||
| + | <td> [[Image:Qsource14.png|thumb|left|450px|The 2D static domain dialog.]] </td> | ||
| + | </tr> | ||
| + | </table> | ||
| − | + | [[Image:Info_icon.png|30px]] Click here to learn more about the theory of '''[[Electrostatic_%26_Magnetostatic_Field_Analysis#2D_Quasi-Static_Solution_of_TEM_Transmission_Line_Structures | 2D Quasi-Static Analysis of Transmission Lines]]'''. | |
| − | + | <table> | |
| + | <tr> | ||
| + | <td> | ||
| + | [[Image:Qsource16.png|thumb|left|480px|A field sensor and 2D solution plane defined for a microstrip line.]] | ||
| + | </td> | ||
| + | </tr> | ||
| + | </table> | ||
| − | + | <table> | |
| + | <tr> | ||
| + | <td> [[Image:Qsource17.png|thumb|left|480px|Electric field distribution of the microstrip line on the 2D solution plane.]] </td> | ||
| + | </tr> | ||
| + | <tr> | ||
| + | <td> [[Image:Qsource18.png|thumb|left|480px|Electric scalar potential distribution of the microstrip line on the 2D solution plane.]] </td> | ||
| + | </tr> | ||
| + | </table> | ||
| − | + | <br /> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | <hr> | |
| − | + | [[Image:Top_icon.png|30px]] '''[[EM.Ferma#Product_Overview | Back to the Top of the Page]]''' | |
| − | + | [[Image:Tutorial_icon.png|30px]] '''[[EM.Cube#EM.Ferma_Documentation | EM.Ferma Tutorial Gateway]]''' | |
| − | + | [[Image:Back_icon.png|30px]] '''[[EM.Cube | Back to EM.Cube Main Page]]''' | |
| − | + | ||
| − | + | ||
Latest revision as of 16:59, 11 January 2021
Electrostatic, Magnetostatic & Thermal Solvers For DC And Low Frequency Simulations
Contents
- 1 Product Overview
- 2 EM.Ferma Features at a Glance
- 3 Building the Physical Structure in EM.Ferma
- 4 EM.Ferma's Computational Domain
- 5 EM.Ferma's Simulation Data & Observables
- 6 Discretizing the Physical Structure in EM.Ferma
- 7 Running Static Simulations in EM.Ferma
- 8 The 2D Quasi-Static Simulation Mode
Product Overview
EM.Ferma in a Nutshell
EM.Ferma is a 3D static solver. It features two distinct electrostatic and magnetostatic simulation engines and a steady-state thermal simulation engine that can be used to solve a variety of static and low-frequency electromagnetic and thermal problems. The thermal solver includes both conduction and convection heat transfer mechanisms. All the three simulation engines are based on finite difference solutions of Poisson's equation for electric and magnetic potentials and temperature.
With EM.Ferma, you can explore the electric fields due to volume charge distributions or fixed-potential perfect conductors, and magnetic fields due to wire or volume current sources and permanent magnets. Your structure may include dielectric or magnetic (permeable) material blocks. Using the thermal simulator, you can solve for the steady-state temperature distribution of structures that include perfect thermal conductors, insulators and volume heat sources. You can also use EM.Ferma's 2D quasi-static mode to compute the characteristic impedance (Z0) and effective permittivity of transmission line structures with complex cross section profiles.
![]() Click here to learn more about the Theory of Electrostatic and Magnetostatic Methods.
Click here to learn more about the Theory of Electrostatic and Magnetostatic Methods.
![]() Click here to learn more about the Theory of Steady-State Heat Transfer Methods.
Click here to learn more about the Theory of Steady-State Heat Transfer Methods.
EM.Ferma as the Static Module of EM.Cube
EM.Ferma is the low-frequency Static Module of EM.Cube, a comprehensive, integrated, modular electromagnetic modeling environment. EM.Ferma shares the visual interface, 3D parametric CAD modeler, data visualization tools, and many more utilities and features collectively known as CubeCAD with all of EM.Cube's other computational modules.
![]() Click here to learn more about EM.Cube Modeling Environment.
Click here to learn more about EM.Cube Modeling Environment.
Advantages & Limitations of EM.Ferma's Static Simulator
EM.Ferma computes the electric and magnetic fields independent of each other based on electrostatic and magnetostatic approximations, respectively. As a result, any "electromagnetic" coupling effects or wave retardation effects are ignored in the simulation process. In exchange, static or quasi-static solutions are computationally much more efficient than the full-wave solutions of Maxwell's equations. Therefore, for low-frequency electromagnetic modeling problems or for simulation of sub-wavelength devices, EM.Ferma offers a faster alternative to EM.Cube's full-wave modules like EM.Tempo, EM.Picasso or EM.Libera. EM.Ferma currently provides a fixed-cell brick volume mesh generator. To model highly irregular geometries or curved objects, you may have to use very small cell sizes, which may lead to a large computational problem.
EM.Ferma Features at a Glance
Physical Structure Definition
- Perfect electric conductor(PEC) solids and surfaces (Electrostatics)
- Dielectric objects (Electrostatics)
- Magnetic (permeable) objects (Magnetostatics)
- Perfect thermal conductor (PTC) solids and surfaces (Thermal)
- Insulator objects (Thermal)
Sources
- Fixed-potential PEC for maintaining equi-potential metal objects (Electrostatics)
- Volume charge sources (Electrostatics)
- Volume current sources (Magnetostatics)
- Wire current sources (Magnetostatics)
- Permanent magnets (Magnetostatics)
- Fixed-temperature PTC for maintaining iso-thermal objects (Thermal)
- Volume heat sources (Thermal)
Mesh generation
- Fixed-size brick cells
3D Electrostatic & Magnetostatic Simulation
- Finite difference solution of Laplace and Poisson equations for the electric scalar potential with Dirichlet and Neumann domain boundary conditions
- Finite difference solution of Laplace and Poisson equations for the magnetic vector potential with Dirichlet domain boundary conditions
- Calculation of electric scalar potential and electric field
- Calculation of magnetic vector potential and magnetic field
- Calculation of electric flux over user defined flux boxes and capacitance
- Calculation of magnetic flux over user defined flux surfaces and inductance
- Calculation of electric and magnetic energies, Ohmic power loss and resistance
- Parametric sweep with variable object properties or source parameters
2D Quasi-Static Simulation
- 2D Finite difference solution of cross section of transmission line structures
- 3D domain solution as well as 2D solution of a longitudinally infinite version of the structure defined on a 2D plane
- Calculation of electric potential and electric field distribution
- Parametric sweep of transmission line's geometric and material parameters
- Optimization of transmission line's parameters for impedance design
Steady-State Thermal Simulation
- Finite difference solution of Laplace and Poisson equations for the temperature with Dirichlet and Neumann domain boundary conditions
- Calculation of temperature and heat flux density
- Calculation of thermal energy density on field sensor planes
- Calculation of thermal flux over user defined flux boxes
- Calculation of thermal energy
Data Generation & Visualization
- Electric and magnetic field intensity and vector plots on planes
- Electric and magnetic potential intensity plots on planes
- Temperature and heat flux intensity and vector plots on planes
- Electric and magnetic energy density, dissipated power density and thermal energy density plots on planes
- Animation of field and potential plots after parametric sweeps
- Graphs of characteristic impedance and effective permittivity of transmission line structures vs. sweep variables
- Custom output parameters defined as mathematical expressions of standard outputs
Building the Physical Structure in EM.Ferma
Variety of Physical Objects in EM.Ferma
The simplest static problems involve a charge source in the free space that produces an electric field, or a current source in the free space that produces a magnetic field. In such cases, the only applicable boundary conditions are defined at the boundary of the computational domain. As soon as you introduce a dielectric object next to a charge source or a magnetic (permeable) material next to a current source, you have to deal with a complex boundary value problem. In other words, you need to solve the electric or magnetic Poisson equation subject to the domain boundary conditions as well as material interface boundary conditions. The simplest thermal problem involves one or more thermal plates held at fixed temperatures. Once you introduce material blocks, you have to enforce conductive and convective boundary conditions at the interface between different materials and air. EM.Ferma uses the Finite Difference (FD) technique to find a numerical solution of your static boundary value problem.
EM.Ferma offers the following types of physical objects:
| Icon | Physical Object Type | Applications | Geometric Object Types Allowed | Notes & Restrictions |
|---|---|---|---|---|
| |
Fixed-Potential Perfect Electric Conductor (PEC) | Modeling perfect metals with a fixed voltage | Solid and surface objects | Can be considered an electric source if the fixed voltage is nonzero |
| |
Dielectric/Magnetic Material | Modeling any homogeneous or inhomogeneous material | Solid objects | non-source material |
| |
Volume Charge | Modeling volume charge sources with a fixed charge density or an expression in the global coordinates (x,y,z) | Solid objects | Acts as an electric source |
| |
Volume Current | Modeling volume current sources with a fixed volume current density vector or expressions in the global coordinates (x,y,z) | Solid objects | Acts as a magnetic source |
| |
Permanent Magnet | Modeling permanent magnet sources with a fixed magnetization vector or expressions in the global coordinates (x,y,z) | Solid objects | Acts as a magnetic source |
| |
Wire Current | Modeling wire current sources | Line and polyline objects | Acts as a magnetic source |
| |
Fixed-Temperature Perfect Thermal Conductor (PTC) | Modeling isothermal surfaces with a fixed temperature | Solid and surface objects | Can be considered a thermal source if the fixed temperature is different than the ambient temperature (shares the same navigation tree node as PEC object) |
| |
Insulator Material | Modeling any homogeneous or inhomogeneous material | Solid objects | non-source material (shares the same navigation tree node as dielectric material) |
| |
Volume Heat Source | Modeling volume heat sources with a fixed heat density or an expression in the global coordinates (x,y,z) | Solid objects | Acts as a thermal source (shares the same navigation tree node as volume charge) |
| |
Virtual Object | Used for representing non-physical items | All types of objects | None |
Click on each category to learn more details about it in the Glossary of EM.Cube's Materials, Sources, Devices & Other Physical Object Types.
Grouping Objects by Material or Source Type
Your physical structure in EM.Ferma is typically made up of some kind of source object either in the free space or in the presence of one or more material objects. EM.Ferma's electrostatic and magnetostatic or thermal simulation engines then discretize the entire computational domain including these source and material objects and solve the Laplace or Poisson equations to find the electric or magnetic fields or temperature everywhere in the computational domain.
All the geometric objects in the project workspace are organized together into object groups which share the same properties including color and electric or magnetic parameters. It is recommended that you first create object groups, and then draw new objects under the active group. To create a new object group, right-click on its category name in the "Physical Structure" section of the navigation tree and select one of the "Insert New Group..." items from the contextual menu. However, if you start a new EM.Ferma project from scratch, and start drawing a new object without having previously defined any object groups, a new default "Fixed-Potential PEC" object group with a zero voltage is created and added to the navigation tree to hold your new geometric object.
It is important to note that there is a one-to-one correspondence between electrostatic and thermal simulation entities:
| Electrostatic Item | Corresponding Thermal Item |
|---|---|
| Electric Scalar Potential | Temperature |
| Electric Field | Heat Flux Density |
| Perfect Electric Conductor | Perfect Thermal Conductor |
| Dielectric Material | Insulator Material |
| Volume Charge | Volume Heat Source |
Once a new object group node has been created in the navigation tree, it becomes and remains the "Active" object group, which is always listed in bold letters. When you draw a new geometric object such as a box or a sphere, its name is added under the currently active object group. There is only one object group that is active at any time. Any group can be made active by right-clicking on its name in the navigation tree and selecting the Activate item of the contextual menu.
![]() Click here to learn more about Moving Objects among Different Groups.
Click here to learn more about Moving Objects among Different Groups.
A Note on Material and Source Types in EM.Ferma
In EM.Cube's other modules, material types are categorized under the "Physical Structure" section of the navigation tree, and sources are organized under a separate "Sources" section. In those modules, all the geometric objects you draw in your project workspace typically represent material bodies. All of EM.Cube modules except for EM.Ferma require at least one excitation source to be selected from the "Sources" section of the navigation tree before you can run a simulation.
In EM.Ferma, materials and sources are all lumped together and listed under the "Physical Structure" section of the navigation tree. In other words, there is no separate "Sources" section. For example, you can define default zero-potential perfect electric conductors (PEC) in your project to model metal objects. You can also define fixed-potential PEC objects with a nonzero voltage, which can effectively act as a voltage source for your boundary value problem. In this case, you will solve the Lapalce equation subject to the specified nonzero potential boundary values. Both types of PEC objects are defined from the same PEC node of the navigation tree by assigning different voltage values. Charge and current sources are also defined as geometric objects, and you have to draw them in the project workspace just like other material objects.
EM.Ferma's Computational Domain
The Domain Box
In EM.Ferma, the Poisson or Laplace equations are solved subject to boundary conditions using the Finite Difference technique. As a result, you need to specify a finite computational domain and then specify the domain boundary conditions. EM.Ferma's computational domain defines where the domain boundary condition will be specified. A default domain box is always placed in the project workspace as soon as you draw your first object. The domain can be seen as a blue cubic wireframe that surrounds all of the CAD objects in the project workspace.
To modify the domain settings, click the Domain button of the Simulate Toolbar or right-click on "3D Static Domain" entry in the Navigation Tree and select "Domain Settings..." from the contextual menu. In the Domain Settings Dialog, the computational domain can be defined in two different ways: Default and Custom. The default type places an enclosing box with a specified offset from the largest bounding box of your project's CAD objects. The default offset value is 20 project units, but you can change this value arbitrarily. The custom type defines a fixed domain box by specifying the coordinates of its two opposite corners labeled Min and Max in the world coordinate system.
Domain Boundary Conditions
- EM.Ferma allows you to specify the electric potential boundary conditions on the domain box. Two options are available. The Dirichlet boundary condition is the default option and is specified as a fixed potential value on the surface of the domain walls. By default, this value is 0 Volts. The Neumann boundary condition specifies the normal derivative of the electric scalar potential on the surface of the domain walls. This is equivalent to a constant normal electric field component on the domain walls and its value is specified in V/m.
- The magnetostatic simulation engine always assumes Dirichlet domain boundary conditions and sets the values of the magnetic vector potential to zero on all the domain walls.
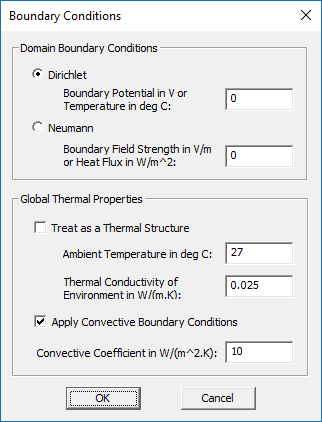
- EM.Ferma provides two options for thermal boundary conditions on the domain box. The Dirichlet boundary condition is the default option and is specified as a fixed temperature value on the surface of the domain walls. By default, this value is 0°C. The Neumann boundary condition specifies the normal derivative of the temperature on the surface of the domain walls. This is equivalent to a constant heat flux passing through the domain walls and its value is specified in W/m2. A zero heat flux means a perfectly insulated domain box and is known as the adiabatic boundary condition.
To modify the boundary conditions, right-click on "Boundary Conditions" in the navigation tree, and select "Boundary Conditions..." from the contextual menu to open the Boundary Conditions Dialog. When you switch from the electrostatic-magnetostatic solver to the thermal solver in EM.Ferma's Run Simulation dialog, it automatically checks the box labeled Treat as a Thermal Structure in the Boundary Conditions dialog. Conversely, if you check this box in the Boundary Conditions dialog, the solver type is set to the thermal solver in the Simulation Run dialog. In the "Global Thermal Properties" section of the Boundary Conditions dialog, you can set the values of the ambient temperature in °C, thermal conductivity of the environment in W/(m.K) and the convective coefficient in W/(m2.K). You can also disable the enforcement of the convective boundary condition on the surface of solid insulator objects.
EM.Ferma's Simulation Data & Observables
At the end of an electrostatic simulation, the electric field vector and electric scalar potential values are computed at all the mesh grid points of the entire computational domain. At the end of an magnetostatic simulation, the magnetic field vector and magnetic vector potential values are computed at all the grid nodes. At the end of a thermal simulation, the temperature and heat flux vector are computed at all the mesh grid points of the entire computational domain.
Besides the electric and magnetic fields and temperature, EM.Ferma can compute a number of field integral quantities such as voltage, current, flux, energy, etc. The field components, potential values and field integrals are written into output data files and can be visualized on the screen or graphed in Data Manager only if you define a field sensor or a field integral observable. In the absence of any observable defined in the navigation tree, the static simulation will be carried out and completed, but no output simulation data will be generated.
EM.Ferma offers the following types of output simulation data:
| Icon | Simulation Data Type | Observable Type | Applications |
|---|---|---|---|
| |
Near-Field Distribution Maps | Near-Field Sensor | Computing electric and magnetic field components, electric scalar potential and magnitude of magnetic vector potential on a planar cross section of the computational domain |
| |
Electric and Magnetic Energy and Dissipated Power Density Maps | Near-Field Sensor | Computing electric and magnetic energy densities and dissipated power density on a planar cross section of the computational domain |
| |
Temperature and Heat Flux Distribution Maps | Near-Field Sensor | Computing temperature and heat flux components on a planar cross section of the computational domain |
| |
Thermal Energy Density Maps | Near-Field Sensor | Computing thermal energy density on a planar cross section of the computational domain |
| |
Field Integral Quantities | Static Field Integral | Computing line, surface and volume integrals of the electric and magnetic fields and heat flux |
Click on each category to learn more details about it in the Glossary of EM.Cube's Simulation Observables & Graph Types.
The table below list the different types of field integrals and their definitions:
| Field Integral | Definition | Output Data File |
|---|---|---|
| Voltage | [math] V = - \int_C \mathbf{E(r)} . \mathbf{dl} [/math] | voltage.DAT |
| Current | [math] I = \oint_{C_o} \mathbf{H(r)} . \mathbf{dl} [/math] | current.DAT |
| Conduction Current | [math] I_{cond} = \int\int_S \mathbf{J(r)} . \mathbf{ds} = \int\int_S \sigma \mathbf{E(r)} . \mathbf{ds} [/math] | conduction_current.DAT |
| Electric Flux | [math] \Phi_E = \int\int_{S_o} \mathbf{D(r)} . \mathbf{ds} = \int\int_{S_o} \epsilon \mathbf{E(r)} . \mathbf{ds} [/math] | flux_E.DAT |
| Magnetic Flux | [math] \Phi_H = \int\int_S \mathbf{B(r)} . \mathbf{ds} = \int\int_S \mu \mathbf{H(r)} . \mathbf{ds} [/math] | flux_H.DAT |
| Electric Energy | [math] W_E = \frac{1}{2} \int \int \int_V \epsilon \vert \mathbf{E(r)} \vert ^2 dv [/math] | energy_E.DAT |
| Magnetic Energy | [math] W_H = \frac{1}{2} \int\int\int_V \mu \vert \mathbf{H(r)} \vert ^2 dv [/math] | energy_H.DAT |
| Ohmic Power Loss | [math] P_{ohmic} = \int\int\int_V \sigma \vert \mathbf{E(r)} \vert ^2 dv [/math] | ohmic.DAT |
| Capacitance | [math] C = \Phi_E/V = \int\int_{S_o} \epsilon \mathbf{E(r)} . \mathbf{ds} / \int_C \mathbf{E(r)} . \mathbf{dl} [/math] | capacitance.DAT |
| Capacitance (Alternative) | [math] C = 2W_E/V^2 = 2 \int \int \int_V \epsilon \vert \mathbf{E(r)} \vert ^2 dv / \left( \int_C \mathbf{E(r)} . \mathbf{dl} \right)^2[/math] | capacitance.DAT |
| Self-Inductance | [math] L = \Phi_H/I = \int\int_S \mu \mathbf{H(r)} . \mathbf{ds} / \oint_{C_o} \mathbf{H(r)} . \mathbf{dl} [/math] | inductance.DAT |
| Self-Inductance (Alternative) | [math] L = 2W_M/I^2 = 2 \int \int \int_V \mu \vert \mathbf{H(r)} \vert ^2 dv / \left( \oint_{C_o} \mathbf{H(r)} . \mathbf{dl} \right)^2[/math] | inductance.DAT |
| Mutual Inductance | [math] M = \Phi_H^{\prime}/I = \int\int_{S^{\prime}} \mu \mathbf{H(r)} . \mathbf{ds} / \oint_{C_o} \mathbf{H(r)} . \mathbf{dl} [/math] | mutual_inductance.DAT |
| Resistance | [math] R = V/I_{cond} = - \int_C \mathbf{E(r)} . \mathbf{dl} / \int\int_S \sigma \mathbf{E(r)} . \mathbf{ds} [/math] | resistance.DAT |
| Resistance (Alternative 1) | [math] R = V^2/P_{ohmic} = \left( \int_C \mathbf{E(r)} . \mathbf{dl} \right)^2 / \int\int\int_V \sigma \vert \mathbf{E(r)} \vert ^2 dv [/math] | resistance.DAT |
| Resistance (Alternative 2) | [math] R = P_{ohmic}/I_{cond}^2 = \int\int\int_V \sigma \vert \mathbf{E(r)} \vert ^2 dv / \left( \int\int_S \sigma \mathbf{E(r)} . \mathbf{ds} \right)^2[/math] | resistance.DAT |
| Thermal Flux | [math] \Phi_T = \int\int_{S_o} \mathbf{q(r)} . \mathbf{ds} [/math] | flux_T.DAT |
| Thermal Energy | [math] W_T = Q = \int \int \int_V \rho_V c_p \left( T\mathbf{(r)} - T_{env} \right) dv [/math] | energy_T.DAT |
Discretizing the Physical Structure in EM.Ferma
The Static Mesh
The Finite Difference technique discretizes the computational domain using a 3D rectangular grid. EM.Ferma generates a fixed-cell mesh. This means that the extents of the mesh cells along the principal axes are fixed: Δx, Δy, Δz. By default, the mesh cell size is set to one unit project along all the three directions (with Δx = Δy = Δz). To modify the cell size, click the Mesh Settings button of the Simulate Toolbar or right-click on "Static Mesh" in the Navigation Tree, and select "Mesh Settings..." from the contextual menu to open the Mesh Settings Dialog.
| |
To obtain accurate results, it is highly recommended to use a square mesh as much as possible. |
![]() Click here to learn more about Working with Mesh Generator.
Click here to learn more about Working with Mesh Generator.
![]() Click here to learn more about the properties of EM.Ferma's Fixed-Cell Brick Mesh Generator.
Click here to learn more about the properties of EM.Ferma's Fixed-Cell Brick Mesh Generator.
Running Static Simulations in EM.Ferma
EM.Ferma's Simulation Modes
EM.Ferma currently offers three different simulation modes as follows:
| Simulation Mode | Usage | Number of Engine Runs | Frequency | Restrictions |
|---|---|---|---|---|
| Analysis | Simulates the physical structure "As Is" | Single run | N/A | None |
| Parametric Sweep | Varies the value(s) of one or more project variables | Multiple runs | N/A | None |
| Optimization | Optimizes the value(s) of one or more project variables to achieve a design goal | Multiple runs | N/A | None |
Running an Electrostatic, Magnetostatic or Thermal Analysis
EM.Ferma has three independent but functionally similar static simulation engines: Electrostatic, Magnetostatic and Thermal. The electrostatic engine solves the electric form of Poisson's equation for electric scalar potential subject to electric field boundary conditions, in the presence of electric sources (volume charges and fixed-potential PEC blocks) and dielectric material media. The magnetostatic engine solves the magnetic form of Poisson's equation for magnetic vector potential subject to magnetic field boundary conditions, in the presence of magnetic sources (wire and volume currents and permanent magnetic blocks) and magnetic material media. The thermal engine solves the thermal form of Poisson's equation for steady-state temperature subject to thermal boundary conditions, in the presence of heat sources (volume sources and fixed-temperature PTC blocks) and insulator material media.
To run a static simulation, first you have to open the Run Dialog. This is done by clicking the "Run" button of the Simulate Toolbar, or by selecting the "Run" item of the Simulate Menu, or simply using the keyboard shortcut "Ctrl+R". There are two available options for the simulation engine: Electrostatic-Magnetostatic Solver and Steady-State Thermal Solver. Clicking the Run button of this dialog starts a static analysis. A separate window pops up which reports the progress of the current simulation.
In EM.Ferma you don't have to choose between the electrostatic or magnetostatic simulation engines. The program looks at the types of sources and material objects present in your project workspace and then it determines whether an electrostatic analysis or a magnetostatic analysis or possibly both should be performed. When there are only electric sources present, you will get nonzero electric fields and zero magnetic fields. When there are only magnetic sources present, you will get nonzero magnetic fields and zero electric fields. On the other hand, since the electrostatic and thermal solvers share the same navigation resources, you can run only one of the two engines at a time. By default, the electrostatic solver is enabled.
An "Analysis" is the simplest simulation mode of EM.Ferma. It is a single-shot finite difference solution of your static problem. The physical structure of your project workspace is first discretized using a fixed-cell mesh and the Poisson equation is solved numerically everywhere in the computational domain. The field and potential values at each mesh node are computed, and the specified observables are written into data files. The other available simulation modes, parametric sweep and optimization, involve multiple runs of the static solvers.
Static Simulation Engine Settings
EM.Ferma offers two different types of linear system solver for solving the matrix equations that result from discretization of Poisson's equation: an iterative solver based on the stabilized Bi-Conjugate Gradient (BiCG) method and a Gauss-Seidel solver. The default solver type is BiCG. You can specify some numerical parameters related to the BiCG solver. To do that, you need to open the Simulation Engine Settings Dialog by clicking the "Settings" button located next to the "Select Engine" drop-down list. From this dialog you can set the maximum number of BiCG iterations, which has a default value of 10,000. You can also set a value for "Convergence Error". The default value for electrostatic analysis is 0.001. For magnetostatic analysis, the specified value of convergence error is reduced by a factor 1000 automatically. Therefore, the default convergence error in this case is 10-6.
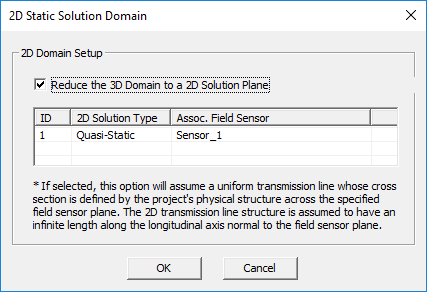
The 2D Quasi-Static Simulation Mode
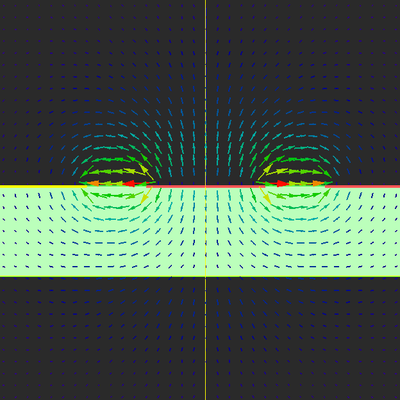
EM.Ferma's electrostatic simulation engine features a 2D solution mode where your physical model is treated as a longitudinally infinite structure in the direction normal to specified "2D Solution Plane". A 2D solution plane is defined based on a "Field Sensor" definition that already exists in your project. To explore EM.Ferma's 2D mode, right-click on 2D Solution Planes in the "Computational Domain" section of the navigation tree and select 2D Domain Settings... from the contextual menu. In the 2D Static Domain dialog, check the checkbox labeled "Reduce the 3D Domain to a 2D Solution Plane". The first field sensor observable in the navigation tree is used for the definition of the 2D solution plane.
At the end of a 2D electrostatic analysis, you can view the electric field and potential results on the field sensor plane. It is assumed that your structure is invariant along the direction normal to the 2D solution plane. Therefore, your computed field and potential profiles must be valid at all the planes perpendicular to the specified longitudinal direction. A 2D structure of this type can be considered to represent a transmission line of infinite length. EM.Ferma also performs a quasi-static analysis of the transmission line structure, and usually provides good results at lower microwave frequencies (f < 10GHz). It computes the characteristics impedance Z0 and effective permittivity εeff of the multi-conductor TEM or quasi-TEM transmission line. The results are written to two output data files named "solution_plane_Z0.DAT" and "solution_plane_EpsEff.DAT", respectively.
![]() Click here to learn more about the theory of 2D Quasi-Static Analysis of Transmission Lines.
Click here to learn more about the theory of 2D Quasi-Static Analysis of Transmission Lines.