RF Tutorial Lesson 9: Designing a Distributed RF BJT Amplifier
Designing a BJT RF Amplifier with Lumped Elements
Contents
- 1 Objective
- 2 Examining the High Frequency BJT Model
- 3 Building the BJT Amplifier and Its DC Bias Circuit
- 4 Stability Analysis of the BJT Transistor & RF Design Strategy
- 5 Designing Input and Output Matching Networks
- 6 Running a Network Analysis of the BJT Amplifier
- 7 Running an AC Frequency Sweep Test of the BJT Amplifier
Objective
In this tutorial, you will build an RF amplifier using a high frequency bipolar junction transistor (BJT) with lumped elements. First, you will examine the S-parameter model of the transistor and analyze its DC bias circuit. Then, you calculate the port characteristics of the amplifier and verify its matching network. Finally, you will run an AC frequency sweep analysis of the amplifier to find its voltage and gain performance.
Examining the High Frequency BJT Model
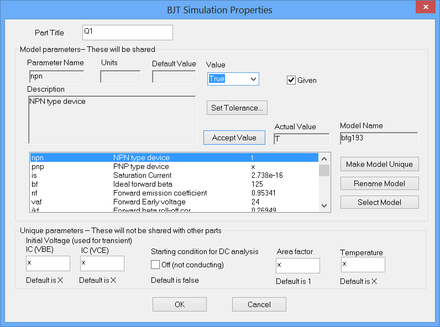
High frequency transistors are typically characterized by their S-parameters. The manufacturer data sheets of RF transistors usually contains tables of measured S-parameter data for various DC bias operating points over a certain range of frequencies. RF.Spice has a large number of RF bipolar junction transistor (BJT) models with measured S-parameter tables for different combinations of collector-emitter voltages (VCE) and collector currents (IC). Most of RF.Spice's RF BJT devices also have counterpart standard BJT model that can be used for DC operating point analysis. The figures below shows the property dialog of the standard BJT model of BFG193 next to the property dialog of the RF BJT model of BFG193 measured at VCE = 10V and IC = 10mA. You will use this transistor for the amplifier design of this tutorial lesson.
You will start this tutorial lesson by testing the S-parameters of BFG193. Open the Parts Bin of the Toolbox and search for BFG193. You can search alphabetically or by function under Active > Transistor > NPN > RF. Place an instance of this BJT on the schematic and place two Net Markers (keyboard shortcut: Alt+N) to designate the base and collector of the BJT as the input and output of your circuit as shown in the opposite figure. Ground the emitter of the BJT. Run a Network Analysis Test of your simple two-port RF circuit. Set the start and stop frequencies of the sweep to 500MHz and 1500MHz, respectively, with a linear frequency step size of 10MHz. Choose "S" parameters on a Cartesian graph with both amplitude and phase and a dB scale. The figure below shows the S-parameter results with magnitudes in dB and phases in degrees. Use the tracking crosshairs of the graph window to read the value of |s21| at 1GHz. The reading at the bottom of the screen shows a value of 12.442dB, which corresponds to 4.187 as you can see from the highlighted row in the S-parameter table of the BJT's property dialog.
| |
The symbols of the standards BJT and its RF counterpart with an S-parameter model are slightly different. |
Building the BJT Amplifier and Its DC Bias Circuit
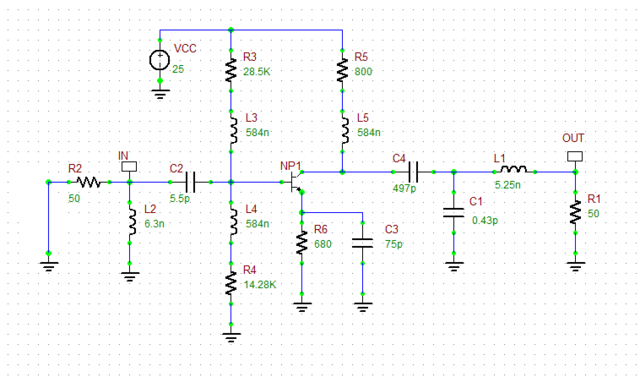
The following is a list of parts needed for this part of the tutorial lesson:
DC Voltage source VCC: 25V (keyboard shortcut: V)
AC Voltage Source: VS (keyboard shortcut: Alt+V)
NPN RF BJT: "Standard" BFG193 Model (Accessible from Parts Bin)
Three RF Chokes: L3 = L4 = L5 = 584nH (keyboard shortcut: L)
DC Blocking Capacitor: C4 = 497pF (keyboard shortcut: C)
DC Bypass Capacitor: C3 = 75pF (keyboard shortcut: C)
Source and Load Resistors: R1 and R2 50Ω
Four DC Bias Resistors: R3 = 28.5k , R4 = 14.28k, R5 = 800Ω and R6 = 680Ω
Tuning Inductors: L1 = 5.25nH and L2 = 6.3nH
Tuning Capacitors: C1 = 0.43pF and C2 = 5.5pF
Two Net Markers: IN and OUT (keyboard shortcut: Alt+N)
Place and connect all the parts as shown in the above figure. Note that for this part you will use the standard BJT model with the "Ideal Forward Beta (BF)" parameter. You need the standard model to perform a DC operating point analysis. The resistors R3 and R4 acts as a voltage divider for power supply VCC. R5 and R6 control and determine the collector and emitter currents, respectively. The RF chokes L3, L4 and L5 pass the DC currents but block the AC signal and effectively remove the resistors R3, R4 and R5 from the RF analysis. The bypass capacitor C3 shorts the resistor R4 in the AC analysis. The DC blocking capacitor C4 isolates the DC bias circuitry form the load but acts as a short circuit for AC analysis. Note that for this circuit, the tuning capacitor C2 also acts as a DC blocking capacitor which isolates the bias circuitry from the AC source.
The DC bias circuit has been designed to generate a collector current of IC = 10mA with a collector-emitter voltage of VCE = 10V. For this reason, you will use the S-parameter RF model BFG193v10v10mA in the next part. Run a DC Bias Test of your BJT amplifier to find its DC operating point parameters. From the results table, you will see:
IC = 10.087mA
VCE = VQC - VQE = 16.933 -6.911 = 10.022V
which validate the DC bias design goals. You can also see all the DC voltages and currents by running a live simulation of the circuit and enabling circuit animation on the Schematic Editor.
Stability Analysis of the BJT Transistor & RF Design Strategy
Before designing the matching networks, first you have to perform a stability analysis of the RF BFG193 transistor at the operating frequency of 1GHz. The table below gives the S-parameter values of this BJT at 1GHz:
| S-parameter | Mag-Phase | Real-Imag |
|---|---|---|
| s11 | 0.4472 ∠166.5° | -0.4348 +j 0.1044 |
| s21 | 4.187 ∠65.1° | 1.7629 + j3.7978 |
| s12 | 0.0960 ∠50.4° | 0.0612 + j0.0740 |
| s22 | 0.2586 ∠-57.0° | 0.1408 - j0.2169 |
To perform a K-Δ stability test of the BJT, we need to calculate the following quantities:
[math] \left| \Delta \right| = \left| s_{11}s_{22} - s_{12}s_{21} \right| = \left| 0.1346 - j0.2539 \right| = 0.2873 [/math]
[math] K = \frac {1 - |s_{11}|^2 - |s_{22}|^2 + |\Delta |^2 } { 2|s_{12}s_{21}| } = 1.0144 [/math]
It can be seen that Rollet's condition, K > 1 and |Δ| <1, is satisfied at 1GHz. So the BFG193 BJT is unconditionally stable at 1GHz with a DC operating condition of VCE = 10V and IC = 10mA.
Although the BJT is not unilateral (s12 ≠ 0), you will adopt a unilateral design strategy and will verify your design outcome later. For this purpose, you will set
[math] \Gamma_S = s_{11}^\ast = -0.4348 -j 0.1044 = 0.4472 \angle -166.5^o [/math]
[math] \Gamma_L = s_{22}^\ast = 0.1408 + j0.2169 = 0.2586 \angle 57.0^o [/math]
where ΓS and ΓL are the source and load reflection coefficients looking to the left and right of the transistor.
Designing Input and Output Matching Networks
Based on the source and load reflection coefficients established in the previous section, you can now design LC matching network sections to be inserted between the based of the BJT and the voltages source and between the collector of the BJT and the load.
For the input matching network you will use a shunt inductor L2 and a series capacitor C2 in conjunction with the source resistor R2. Note that the AC voltage source must be shorted for the calculation of the input reflection coefficient. Set up a simple circuit as shown in the opposite figure and assign a single port between the free node of the series capacitor and the ground. Run a Network Analysis Test of this circuit over 500MHz to 1500MHz with a frequency step size of 500MHz. Choose the "S" Parameter option with Amp/Phase format and only check the "Table" checkbox, not the Graph. This will compute and tabulate the s11 parameter of the matching network at 500MHz, 1GHz and 1.5GHz, as shown in the figure below. Note that at 1GHz the required source reflection coefficient has been achieved.
Next, you will use a shunt capacitor C1 and a series inductor L2 in conjunction with the load resistor R1 for the output matching network. Set up another simple circuit as shown in the opposite figure and assign a single port between the top node of the shunt capacitor and the ground. Run a Network Analysis Test of this circuit, again over 500MHz to 1500MHz with a frequency step size of 500MHz, with the same test settings as before. The s11 parameter of the output matching network is shown in the figure below at 500MHz, 1GHz and 1.5GHz. as you can see from the table, the required load reflection coefficient has been achieved.
Running a Network Analysis of the BJT Amplifier
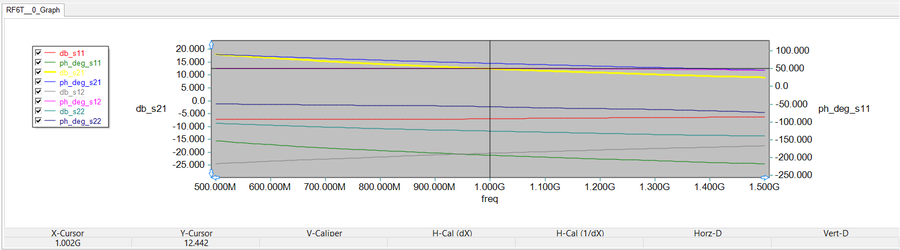
At this point, your BJT amplifier circuit is ready for an overall Network Analysis Test. Replace Q1 (the standard BFG193 model) with NP1 (RF BJT model of BFG193). Place the "IN" marker right after the source resistor, and place the "OUT" marker at the load resistor. Replace the AC voltage source with a piece of wire as shown in the opposite figure. Run a network analysis of this circuit with start and stop frequencies set at 500MHz and 1500MHz and with a linear frequency step size of 10MHz. Plot the S-parameters on an amplitude-only Cartesian graph. The figure below shows the results for s11, s21, s12 and s22 parameters.
| |
For Network Analysis Test, all the AC voltage sources must be short-circuited and all the AC current sources must be open-circuited. |
A tracking crosshair has been used to read the value of |s21| at 1GHz. This value is 8.02dB. Note that the total input reflection coefficient and the total output
reflection coefficient are both below -10dB at 1GHz and the overall |s12| of the circuit is negligible.
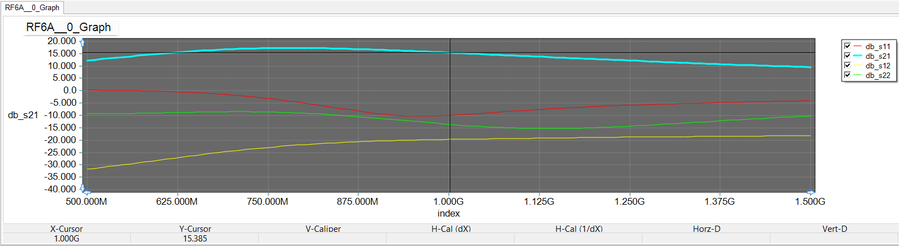
Keep in mind that the results you obtained so far included the source and load resistors. They represent the S-parameters of your overall network. For the purpose of our analysis and comparison with the results of the next part, it is instructive to remove the source and load resistors and run a Network Analysis Test of the true amplifier circuit independent of the source and load. The opposite figure shows this circuit with the source and load sections removed. Run an AC Network Analysis Test of this modified circuit with the exactly the same settings as in the previous case. The results are shown in the figure below. Note how the value of |s21| at 1GHz has jumped to 15.385dB this time around, while the total input and output reflection coefficients are still both below -10dB. This validates your design strategy based on the unilateral assumption. You will see in the next section that the computed values of |s21| (insertion loss or gain) is very close to the computed value of the power gain from the source to the load.
Running an AC Frequency Sweep Test of the BJT Amplifier
In the last part of this tutorial lesson, you will run an AC Sweep Test of your BJT amplifier circuit to examine the input and output voltages and find the voltage gain and power gain of your amplifier. To measure the power gain, we define input and output powers as the source and load powers:
[math] P_{in} = P_S = \frac{1}{2} R_S |I_S|^2 [/math]
[math] P_{out} = P_L = \frac{1}{2} R_L |I_L|^2 [/math]
[math] G_P = \frac{P_L}{P_S} = \left| \frac{I_L}{I_S} \right| ^2 [/math]
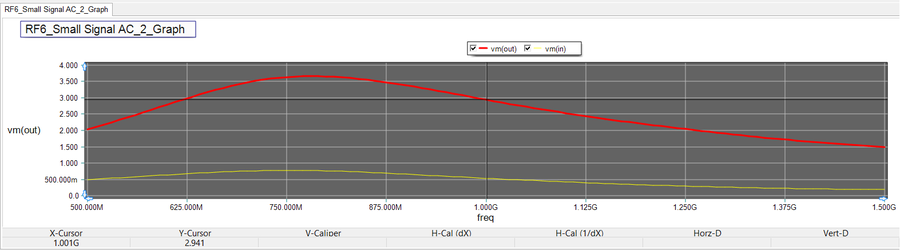
Note that RS = RL = 50Ω. To compute the source and load currents IS and IL, you can place two ammeters (keyboard shortcut: Alt+Y), one between the AC voltage source and the source resistor, and the other just before the load resistor as shown in the opposite figure. Set the start and stop frequencies of the sweep to 500MHz and 1500MHz with a linear frequency step size of 10MHz. Add that the voltage amplitudes vm(in) and vm(out) to the graph plot list in the Edit Plot List dialog. Run the AC sweep, and you will get input and output voltage graphs like the ones shown below. Enable the tracking crosshairs and read the values at 1GHz. Note that when you have multiple plots, the tracking crosshairs read the value of the highlighted (selected) plot. The input and output voltage readings are 2.941V and 535mV, respectively. The input voltage value shows that the default 1V voltage of the source VS has been almost equally divided between the source resistor and the amplifier circuit.
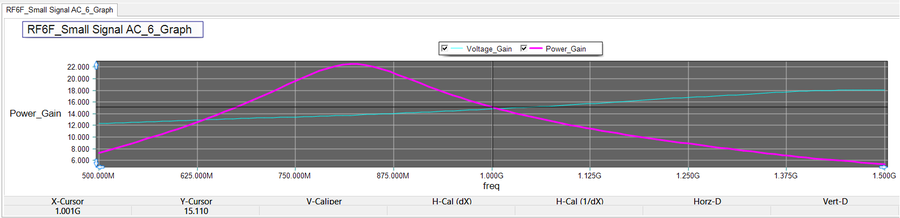
Before closing this tutorial lesson, you will calculate the voltage and power gains of your BJT amplifier. For this purpose, you will define "Custom Output Plots". In the AC Sweep Test Panel, click the "Preset Graph Plots..." button to open the Edit Plot List dialog. Define two new custom output plots with the names "Voltage_Gain" and "Power_Gain" as shown in the figures below. Note that a dB-scale definition has been used. Remove the voltage amplitudes vm(in) and vm(out) from the graph plot list in the Edit Plot List dialog. Run the AC sweep test to plot the voltage and power gain as a function of frequency as shown below. Using the tracking crosshairs read the values of the two gains at 1GHz. The power gain at this frequency is 15.11dB and the voltage gain is almost equal to it. Note that voltage gain rises to a peak around 800MHz, while the power gain rises monotonically. However, both input and output voltages of the amplifier start to decrease with increasing frequency. At 1.5GHz, the output voltage is about 1.5V.