EM.Terrano Tutorial Lesson 2: Examining A Polarimetric Propagation Channel
Contents
- 1 What You Will Learn
- 2 Getting Started
- 3 Setting Up the Scene
- 4 Running an SBR Ray Tracing Analysis
- 5 Visualizing & Analyzing the Individual Rays
- 6 Verifying Your Simulation Results
- 7 Changing the Polarization of the Transmitter and Receiver Antenna
- 8 Changing the Transmitter Height
- 9 Examining the Brewster Angle
What You Will Learn
In this tutorial you will investigate a two-ray scenario that involves ground-reflected rays. You will examine the effect of wave polarization on the reflection characteristics. In this lesson you will use one of EM.Terrano's wizards and will learn how to use project variables.
![]() Back to EM.Terrano Tutorial Gateway
Back to EM.Terrano Tutorial Gateway
![]() Download projects related to this tutorial lesson
Download projects related to this tutorial lesson
Getting Started
Open the EM.Cube application and switch to EM.Terrano. Start a new project with the following attributes:
Setting Up the Scene
For this tutorial lesson, you will use a wizard to build the geometry of a simple communication link consisting of a transmitter and a grid of receivers. Click on the Basic Link Wizard ![]() button of the Wizard Toolbar or select the menu item Tools → Propagation Wizards → Basic Link. A dialog pops up and asks for the total grid extents, transmitter location, transmitter height, receiver height and receiver spacing. Change the grid extents to 50m, change the transmitter and receiver heights both to 2m and change the receiver spacing to 1m. The wizard creates a single transmitter and a very dense grid of 51×51 receivers centered at the origin of coordinates. Note that the wizard automatically creates all the point or array objects necessary for the definition of the transmitter and receiver sets. Later on, you will see that the scene created by the wizard is parameterized and you can easily modify the scene by changing the values of its parameters.
button of the Wizard Toolbar or select the menu item Tools → Propagation Wizards → Basic Link. A dialog pops up and asks for the total grid extents, transmitter location, transmitter height, receiver height and receiver spacing. Change the grid extents to 50m, change the transmitter and receiver heights both to 2m and change the receiver spacing to 1m. The wizard creates a single transmitter and a very dense grid of 51×51 receivers centered at the origin of coordinates. Note that the wizard automatically creates all the point or array objects necessary for the definition of the transmitter and receiver sets. Later on, you will see that the scene created by the wizard is parameterized and you can easily modify the scene by changing the values of its parameters.
As you can see from the scene above, the transmitter is collocated with one of the receivers since they have the same heights.
| |
To move a transmitter or receiver to a new location, you need to move their associated point objects. |
Open the property dialog of the point object "TXP" associated with the transmitter. To do so, select the object's name on the navigation tree, right-click the mouse and select Properties... from the contextual menu. As you can see, its X-, Y- and Z-coordinates are set to "tx_x", "tx_y", and "tx_h", respectively. These are project variables, which were initiated automatically by the wizard. You can simply replace the numeric value of any object property and replace it with a variable name. All the project variables are list in Variables Dialog. This dialog can be accessed by clicking the ![]() button on the Simulate Toolbar or selecting the menu item Simulate → Variables... or simply using the keyboard shortcut Ctrl+B. Select the variable "tx_x" and click the Edit button of the variables dialog to open the Edit Variable dialog. In the box labeled Definition, enter a value of -30 for this variable.
button on the Simulate Toolbar or selecting the menu item Simulate → Variables... or simply using the keyboard shortcut Ctrl+B. Select the variable "tx_x" and click the Edit button of the variables dialog to open the Edit Variable dialog. In the box labeled Definition, enter a value of -30 for this variable.
Alternatively, you could simply change the value of the X-coordinate in the TPX Point Properties dialog to -30 and click the OK button. The point TXP moves to the left of the scene, and so does the rad ball representing your transmitter.
Running an SBR Ray Tracing Analysis
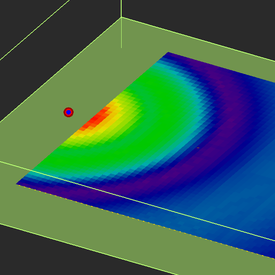
At this time, you are ready to run a SBR simulation. Keep in mind that the default transmitter and receivers type are a vertically polarized (Z-directed) half-wave dipole antenna. Click the Run ![]() button of the Simulate Toolbar to open up the Simulation Run Dialog and state a simulation of the "Single-Frequency Analysis" type. At the end of the simulation, visualize the receiver power coverage map. EM.Cube's View toolbar allows you to view the project workspace from different angles. Click the Top View
button of the Simulate Toolbar to open up the Simulation Run Dialog and state a simulation of the "Single-Frequency Analysis" type. At the end of the simulation, visualize the receiver power coverage map. EM.Cube's View toolbar allows you to view the project workspace from different angles. Click the Top View ![]() button. You can always go back to the perspective view by clicking the Perspective View
button. You can always go back to the perspective view by clicking the Perspective View ![]() button of the view toolbar or using the keyboard shortcut Home.
button of the view toolbar or using the keyboard shortcut Home.
The coverage map clearly shows a pattern of concentric rings that result from constructive and destructive interference between the direct and reflected rays.
Visualizing & Analyzing the Individual Rays
In EM.Terrano, you can visualize all the rays received by each receiver along their entire path starting from the source location. To do that, right click on the Point Receivers item in the navigation tree and select Show Received Rays from the contextual menu. In this case, you will see the two rays received by each receiver: the first is a direct ray from the transmitter to the receiver, and the second is a ray that is reflected off the ground. EM.Terrano allows you to analyze the individual rays.
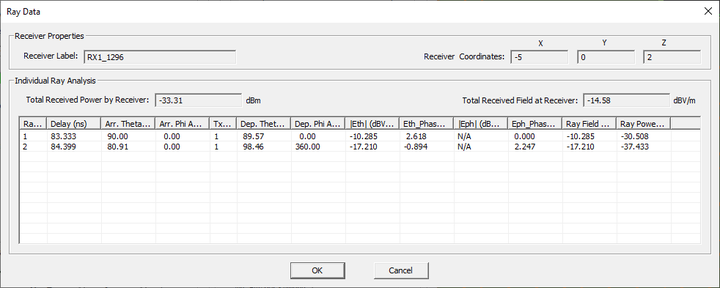
Open the property dialog of your receiver set and select the receiver No. 1296 of the array, which is called "RX1_1296". Then, click the Show Ray Data button to open up the Ray Data Dialog. You will see the two received rays listed along with their delay in nsec, phi and theta angles of arrival in degrees and individual ray’s field value in dBV/m and power value in dBm. The computed received powers of the direct and ground-reflected rays are reported as -30.508dBm and -37.433dBm, respectively. The power of individual rays are calculated based on an isotropic receiver with unity gain.
The table below summarizes the important properties of the two rays:
| Direct Ray | Ground-Reflected Ray | |
|---|---|---|
| Delay | 83.333 ns | 84.399 ns |
| Theta Angle of Arrival | 90° | 80.91° |
| Phi Angle of Arrival | 0 | 0 |
| Ray Field Strength | -10.285 dBV/m | -17.210 dBV/m |
| Ray Power | -30.508 dBm | -37.433 dBm |
Verifying Your Simulation Results
The ray diagram below shows the direct and ground-reflected rays emanating from the transmitter and reaching the selected receiver. It identifies all the necessary distances and angles to calculate the characteristics of the receiver rays.
The delay and power of the direct ray are calculated as follows and agree well with the ray tables of both vertical and horizontal polarizations:
[math] {r_0} = \sqrt{D^2 +(h_T-h_R)^2} = 25\text{m} [/math]
[math] \Delta t_d = \frac{r_0}{c_0} = \frac{25}{3\times10^8} = 83.33\text{ns} [/math]
[math] P_{dir} = EIRP_{dB} + G_{r,dB} + 20log_{10}\left( \frac{\lambda_0}{4\pi r} \right) = 29.88 + 0 + 20log_{10}\left( \frac{0.3}{(4\pi)(25)} \right) = -30.508\text{dBm}[/math]
The ground-reflected ray first traverses a distance of r1 from the transmitter to the specular point. Then, it undergoes reflection off the ground, and the reflected ray traverses a distance of r2 from the specular point to the receiver. The total optical path length is r1 + r2. To find the specular point and the lengths r1 and r2, note the geometric relation:
[math] \frac{h_T}{D_s} = \frac{h_R}{D - D_s} [/math]
With D = 19m and hT = 10m and hR = 1.5m, you find that:
[math] D_s = \frac{h_T D}{h_T + h_R} = 12.5\text{m} [/math]
[math] r_1 = \sqrt{h_T^2 +D_s^2} = 12.659\text{m} [/math]
[math] r_2 = \sqrt{h_R^2 +(D-D_s)^2} = 12.659\text{m} [/math]
[math] r_{tot} = r_1 + r_2 = 25.318\text{m} [/math]
The propagation delay of the reflected ray is therefore found to be:
[math] \Delta t_r = \frac{r_1+r_2}{c_0} = 84.39\text{ns} [/math]
The reflected ray's Theta angle of arrival is the same as the incident angle:
[math] \theta_A = \theta_i = \arctan \left( \frac{h_R}{D-D_s} \right) = 80.91^o [/math]
The reflected ray received by the receiver can be thought of as if it was launched from the image of the transmitter in the ground (with respect to Z = 0). The reflection coefficient at the specular point depends on the wave polarization. In the case of a vertically polarized (Z-directed) transmitter antenna, we have the so-called parallel polarization with the electric field parallel to the plane of incidence. In the case of a horizontally polarized (Y-directed) transmitter antenna, we have the so-called perpendicular polarization with the electric field normal to the plane of incidence. The reflection coefficients for both polarization case are given by:
[math] R_v = R_{\|} = \frac{\eta_1 \cos\theta_t - \eta_0 \cos\theta_i }{ \eta_1 \cos\theta_t + \eta_0 \cos\theta_i } [/math]
[math] R_h = R_{\perp} = \frac{\eta_1 \cos\theta_i - \eta_0 \cos\theta_t }{ \eta_1 \cos\theta_i + \eta_0 \cos\theta_t } [/math]
where
[math] \eta_1 = \eta_0 \sqrt{\frac{\mu_{r1}}{\epsilon_{r1}}} [/math]
The angles θi and θt are the incident and transmitted ray angles as shown in the figure, and the latter angle is calculated from Snell’s law:
[math] k_0 \sin\theta_i = k_1 \sin\theta_t \quad\quad k_1 = k_0 \sqrt{\mu_{r1} \epsilon_{r1}} [/math]
For this scene, you have η1 = η0/√5 = 0.4472η0, k1 = k0√5 = 2.236k0.
[math] \theta_t = \arcsin \left( \frac{k_0}{k_1} \sin\theta_i \right) = 26.21^o [/math]
[math] R_v = \frac{0.4472\cos(26.21^o) - \cos(80.91^o)}{ 0.4472\cos(26.21^o) + \cos(80.91^o) } = 0.435[/math]
[math] R_h = \frac{0.4472\cos(80.91^o) - \cos(26.21^o)}{ 0.4472\cos(80.91^o) + \cos(26.21^o) } = -0.854[/math]
The powers of the reflected rays in the two cases of vertical and horizontal polarizations are then calculated as:
[math] P_{ref,v} = EIRP_{dB} + G_{r,dB} + 20log_{10}\left( \frac{\lambda_0}{4\pi r_{tot}} \right) + 20log_{10} |R_v | = 29.88 + 0 + 20log_{10}\left( \frac{0.3}{(4\pi)(25.318)} \right) + 20log_{10} (0.435) = -37.86\text{dBm}[/math]
[math] P_{ref,h} = EIRP_{dB} + G_{r,dB} + 20log_{10}\left( \frac{\lambda_0}{4\pi r_{tot}} \right) + 20log_{10} |R_h | = 29.88 + 0 + 20log_{10}\left( \frac{0.3}{(4\pi)(25.318)} \right) + 20log_{10} (0.854) = -32.00\text{dBm}[/math]
The analytical results agree well with the ray tracing simulation results.
| |
The ray fields are complex-valued. The total ray field at the receiver location is computed as the coherent sum of the complex-valued fields of all the individual received rays. |
Changing the Polarization of the Transmitter and Receiver Antenna
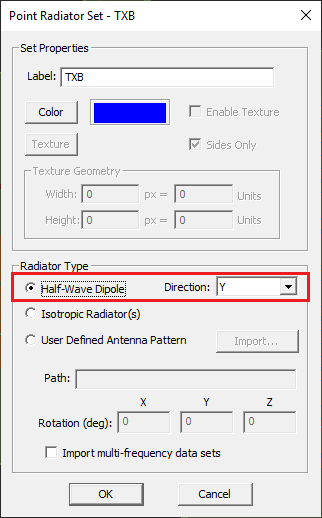
The previous results were obtained using a vertically (Z-directed) polarized half-wave dipole transmitter and receiver. Now, you will see what happens if you change the polarization of the transmitter antenna and the receiver. Open the property dialog of the point radiator set associated with the transmitter (TXB) from the navigation tree. In the section entitled "Radiator Type", choose the option "Y" from the drop-down list labeled Direction next to the radio button Half-Wave Dipole, which has already been selected. Similarly, open the property dialog of the point radiator associated with the receivers (RXB) and change the polarization of the receivers to Y-directed horizontal.
Run a single-frequency SBR analysis of your scene and visualize the received power coverage map. You will see that the pattern of the map has changed with respect to the previous case of vertical polarization.
Open the property dialog of your receiver set once again and select the receiver No. 1296 of the array, which is called "RX1_1296". Open the rays property dialog. The computed Total Received Powers of the direct and ground-reflected rays in this case are reported as -30.508dBm and -31.894dBm, respectively.
The table below summarizes the important properties of the two rays:
| Direct Ray | Ground-Reflected Ray | |
|---|---|---|
| Delay | 83.333 ns | 84.399 ns |
| Theta Angle of Arrival | 90° | 80.91° |
| Phi Angle of Arrival | 0 | 0 |
| Ray Field Strength | -10.285 dBV/m | -11.670 dBV/m |
| Ray Power | -30.508 dBm | -31.894 dBm |
Next, keep the polarization of the transmitter to Y-directed horizontal and change the polarization of the receivers to Z-directed vertical (cross-pol) and run a new SBR analysis.
Changing the Transmitter Height
Earlier you saw that the Z-coordinate of the transmitter's base point (TXP) was set equal to "tx_h" by the wizard. Open the Variables Dialog and change the value of “tx_h” to 10.
Close the dialogs to return to the project workspace. You will see the transmitter raise to a height of 10m. Keep in mind that instead of using the variables, you could have simply changed the Z-coordinate of the point object TXP to 10m from its property dialog.
Open the point radiator set dialog associated with the transmitter and receiver and set the radiators type back to a Z-directed (vertically polarized) half-wave dipole. Run a single-frequency SBR analysis of your scene and visualize the received power coverage map.
From the results of this section, you can see that as you increase the height of the transmitter above the ground, more interference rings appear in the coverage maps.
Examining the Brewster Angle
In the case of parallel polarization, at a certain distance between the transmitter and receiver, the ground-reflected ray may experience the Brewster angle. In that case, the reflected ray theoretically vanishes. The Brewster angle is given by:
[math] \theta_B = \theta_A = \arctan \left( \sqrt{\epsilon_r} \right) = \arctan \left( \sqrt{5} \right) = 65.9^o [/math]
From the ray diagram of the previous section, we can find the following geometrical relationship:
[math] \tan(\theta_B) = \frac{D_s}{h_T} = \frac{D-D_s}{h_R} [/math]
From which the distance between the transmitter and the receiver subject to the Brewster angle can be found:
[math] D_s = h_T \sqrt{5} = 22.36\text{m}[/math]
[math] D-D_s = h_R \sqrt{5} = 4.47\text{m}[/math]
[math] D = 22.36+4.47 = 26.83\text{m}[/math]
In this tutorial lesson, the parallel polarization is the case of the vertically polarized (Z-directed) dipole transmitter. On the X-axis, the closest receiver to have a horizontal distance D = 26.83m from the transmitter is receiver No. 1298: xB = xT + D = -30 + 26.83 = -3.17m. If you open the ray data dialog of this receiver, you will notice that the total electric field intensity and power of the ground-reflected ray in this case are extremely small.
Also note that you cannot distinguish the receiver with the Brewster angle in the coverage map you got earlier. The reason is the coverage map represents the total received power by the receiver. However, the power of the direct ray overshadows the power of the ground-reflected ray. EM.Terrano allows you to include or exclude certain types of rays in your SBR simulation. To see this, open the Simulation Run dialog, and click the Settings next to the engine type drop-down list. The SBR Simulation Engine Settings Dialog opens up. In the lower section of this dialog, check the box labeled Exclude the Direct (LOS) Rays from Solution.
Close the engine settings dialog and run a new SBR simulation. At the end of the simulation, visualize the received power coverage map. This time you will see the coverage map corresponding to the ground-reflected rays, with all the direct rays excluded from the solution. You can clearly see the dark ring centered at the transmitter with a radius of about 27m. All the receivers located on this ring experience the Brewster angle.