EM.Picasso Tutorial Lesson 5: Analyzing Patch Antenna Arrays
Contents
- 1 What You Will Learn
- 2 Getting Started
- 3 Creating the Periodic Patch Unit Cell
- 4 Running a Periodic PMOM Analysis of the Unit Call Structure
- 5 Steering the Beam of the Periodic Patch Array
- 6 Building a Finite-Sized Probe-Fed Patch Array
- 7 Running a PMOM Analysis of the Finite-Sized Patch Array
- 8 Shaping the Beam of the Finite-Sized Patch Array
- 9 Steering the Beam of the Finite-Sized Patch Array
- 10 Examining the Phase of the Radiating Elements
What You Will Learn
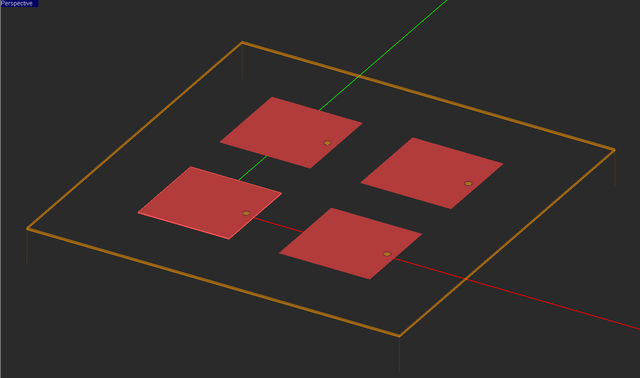
A patch antenna array is typically made up of Nx × Ny individual patch antennas (radiating elements) arranged on a rectangular grid with a uniform spacing of Sx and Sy along the X and Y directions, respectively. You can model patch antenna arrays in a number of different ways:
- Analyze a single isolated patch antenna and use an array factor for radiation pattern calculation. But this method ignores all the inter-element coupling effects.
- Analyze an infinite periodic patch structure and use an array factor for radiation pattern calculation. This method accounts for the inter-element coupling effects, but it cannot capture edge and corner effects.
- Construct a finite-sized Nx × Ny patch array on a finite-sized substrate. This is a full-wave treatment of the antenna array structure but it may prove computationally very expensive.
In this tutorial you will try out the second and third methods from the above list and model a finite-sized probe-fed patch array structure.
![]() Back to EM.Picasso Tutorial Gateway
Back to EM.Picasso Tutorial Gateway
![]() Download projects related to this tutorial lesson
Download projects related to this tutorial lesson
Getting Started
Open the EM.Cube application and switch to EM.Picasso. Start a new project with the following parameters:
In this tutorial lesson, you will model a 4 × 4 array of probe-fed patch antennas. At an operating frequency of 1.575GHz, the free-space wavelength is about 190mm. Your patch array will have a uniform spacing of Sx = Sy = λ0/2 = 95mm in both X and Y directions.
Creating the Periodic Patch Unit Cell
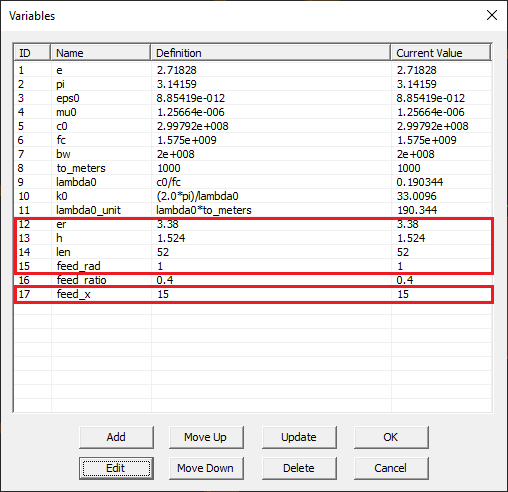
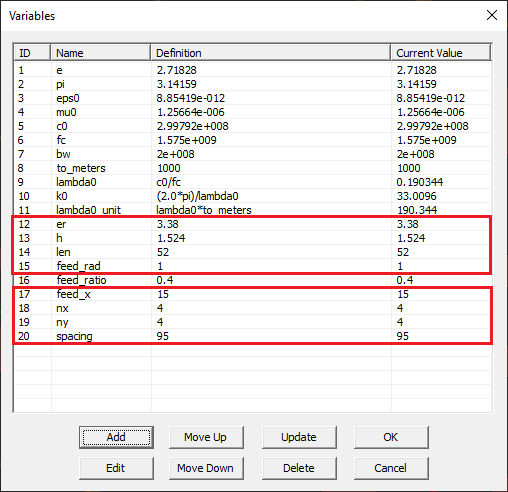
To create a periodic unit cell consisting of a probe-fed patch antenna, repeat the same procedure at the beginning of Tutorial Lesson 4. Use the Probe-Fed Patch Wizard to draw the geometry of the basic antenna structure. Open the variables dialog and change the definition of the following variables:
| Variable Name | Original Definition | New Definition |
|---|---|---|
| er | 2.2 | 3.38 |
| h | 0.0015*to_meters | 1.524 |
| len | 0.48*lambda0_unit/sqrt(er) | 52 |
| feed_rad | 0.0025*to_meters | 1 |
| feed_x | feed_ratio*len | 15 |
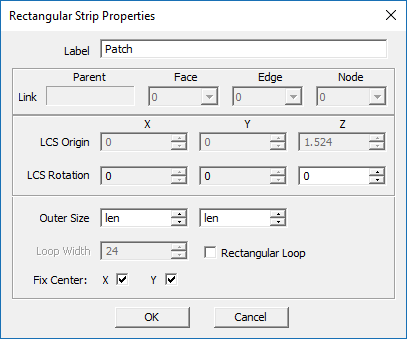
At this point, you have a PEC group called PEC_1 and a PEC Via group called "PECVIA_1" in the navigation tree with the following geometric objects, open the property dialog of the patch object "ANCHOR" and via object "Probe_feed" and make the changes shown in the figures below:
| Object | Geometry | Trace Group | Dimensions | LCS Coordinates | Rotation Angles |
|---|---|---|---|---|---|
| ANCHOR | Rectangle Strip | PEC_1 | len × len | (0, 0, 1.524mm) | (0°, 0°, 0°) |
| Probe_feed | Circle Strip | VIA_FEED | radius = 1mm | (feed_x, 0, 0) | (0°, 0°, 0°) |
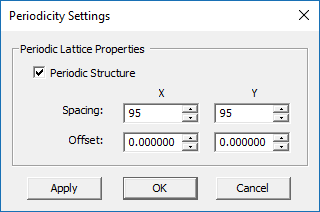
Next, open EM.Picasso's periodicity settings dialog by right-clicking on the Periodicity item of the navigation tree and selecting Periodicity Settings... from the contextual menu. Check the box labeled Periodic Structure and set the value of the Spacing parameter equal to 95mm along both X and Y directions. At the operational frequency of 1.575GHz with a free-space wavelength of λ0 = 190mm, this gives a half-wavelength element spacing.
Once you close the periodicity settings dialog and return to the project workspace, you will notice that the domain box has shrunk to the extents of a single unit cell, and its side walls are drawn with blue dashed lines.
You are going to keep the probe source "PS_1" and the current distribution observable "CD_1" the wizard create for you without any changes. Next, open the property dialog of the far-field observable "FF_1" to change some of the radiation pattern parameters. Set the Angle Increment to 1° for both Theta and Phi angles. In the Array Factor section of the dialog, define a 4×4 array with equal X and Y spacing of 95mm as shown in the figure below. Note that default values of the array spacing along the X and Y directions have automatically been set by EM.Picasso to the periods along those directions.
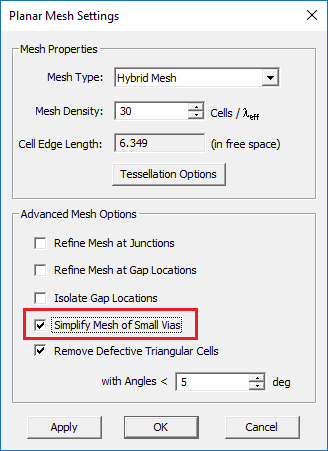
The wizard set the mesh density equal to 30 cells/λeff. Checkmark the "Simplify Mesh of Small Vias" checkbox.
Running a Periodic PMOM Analysis of the Unit Call Structure
Run a quick single-frequency PMOM analysis of your periodic patch array. At the end of the simulation, the port characteristics are reported as:
S11: 0.103832 -0.623762j
S11(dB): -3.980919
Z11: 25.169482 -52.320437j
Y11: 0.007467 +0.015521j
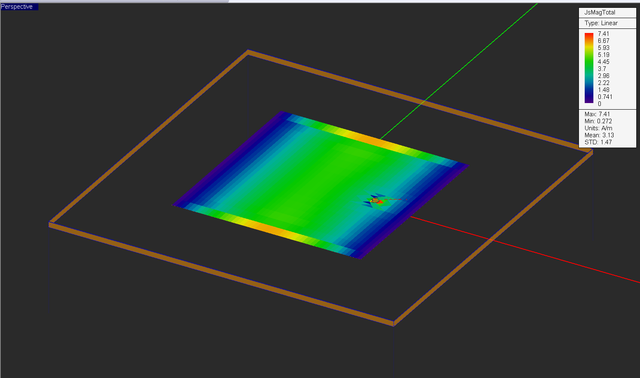
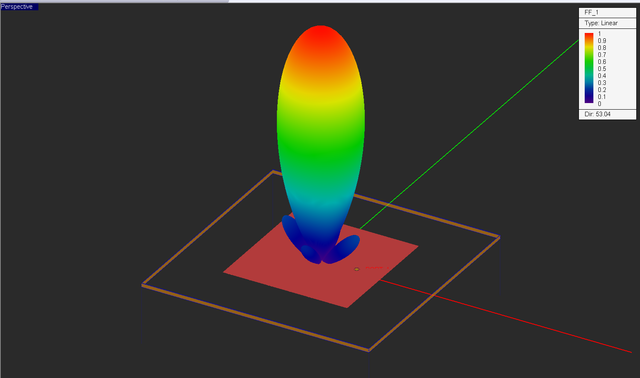
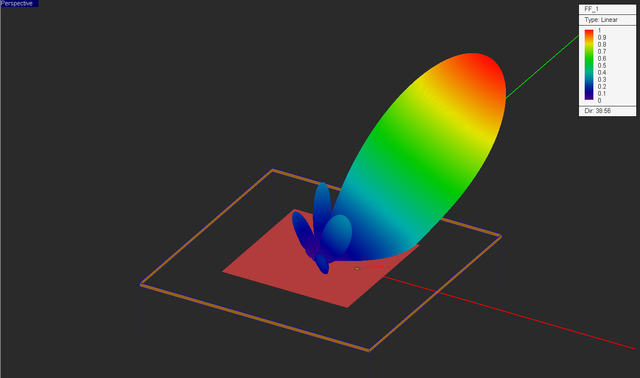
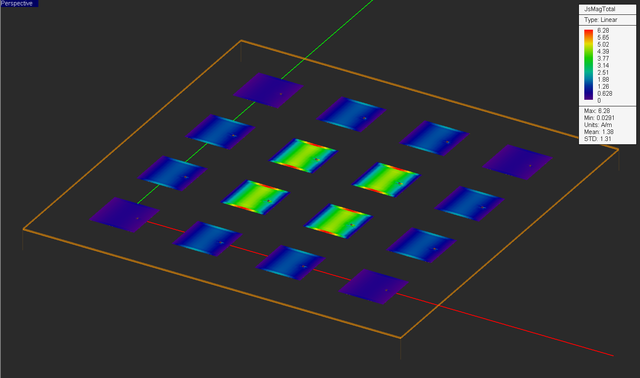
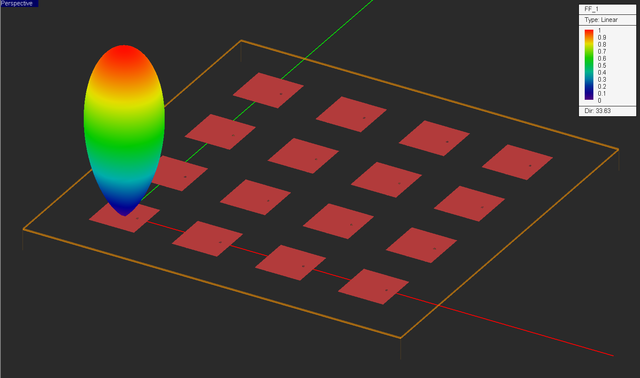
Visualize the current distribution and 3D radiation pattern of your antenna. Note that the computed radiation pattern is the product of a 4×4 array factor and the radiation pattern of the periodic patch unit cell. A high directivity value of D0 = 53.04 (or 17.25dB) is predicted.
Steering the Beam of the Periodic Patch Array
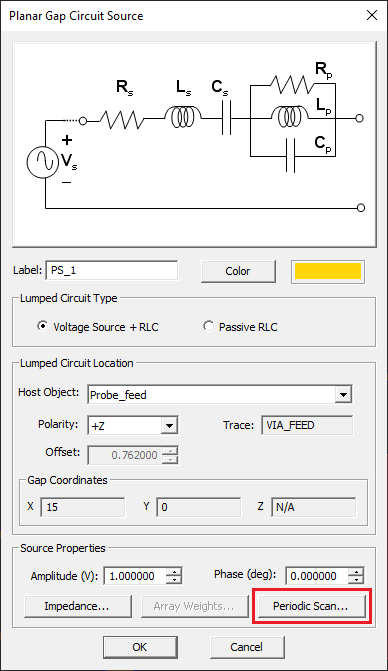
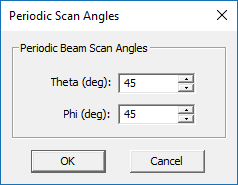
EM.Picasso allows you to steer or scan the beam of a periodic antenna array in any Theta and Phi direction. In EM.Picasso, you can do this with periodic strip and probe gap sources through their property dialog. Open the property dialog of the probe source "PS_1". At the bottom of this dialog, click the button labeled Periodic Scan.... In the Periodic Scan Angles dialog, you can enter values for "Theta (deg)" and "Phi (deg)" in degrees. Their default values are zero. This means that by default there is no phase progression among the elements of the infinite periodic array.
In order to steer the beam of an antenna array to the spherical angles (θ, φ), a two-dimensional phase progression among the array elements is required along the X and Y directions given by the following equations:
[math]\Psi_x = -\frac{2\pi S_x}{\lambda_0} \sin\theta \cos\phi[/math]
[math]\Psi_y = -\frac{2\pi S_y}{\lambda_0} \sin\theta \sin\phi[/math]
where Sx and Sy are the element spacing along the X and Y directions, respectively. In this project, Sx = Sy = λ0/2. The phase progression is therefore given by:
[math]\Psi_x = - \pi \sin\theta cos\phi[/math]
[math]\Psi_y = - \pi \sin\theta sin\phi[/math]
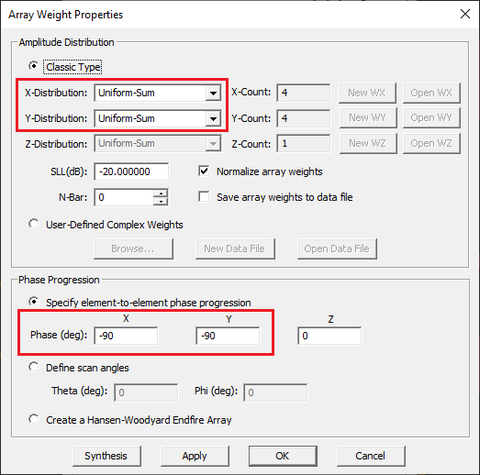
In order to steer the array beam to θ = φ = +45°, you need phase progressions equal to Ψx = Ψy = -90° that is equal phase progression along both X and Y directions. Enter a value of 45 degrees for both "Theta (deg)" and "Phi (deg) in the Periodic Scan Angles dialog and return to the probe source dialog.
Run a PMOM analysis of your periodic array with steered beam. At the end of the simulation, the port characteristics are reported as:
S11: 0.080215 -0.702658j
S11(dB): -3.008887
Z11: 18.654343 -52.447612j
Y11: 0.006020 +0.016925j
Now visualize the 3D radiation pattern of the array with the steered beam.
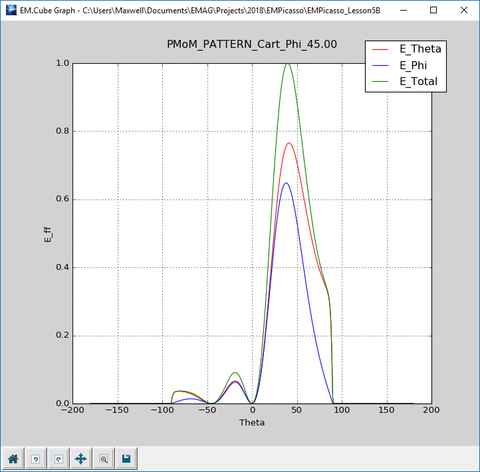
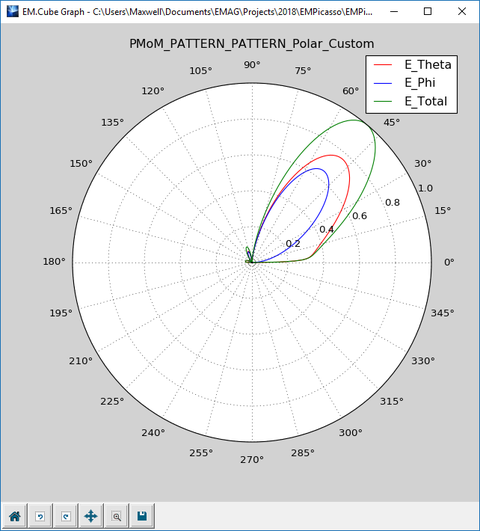
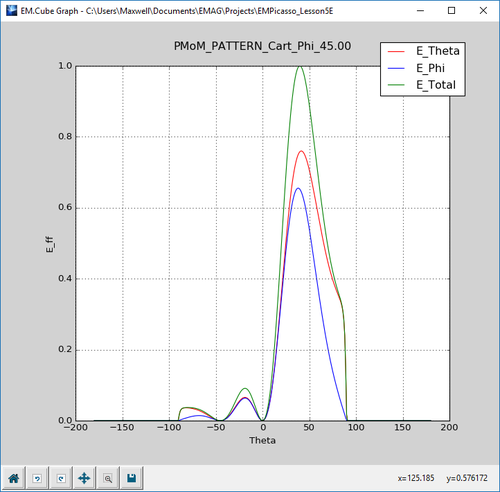
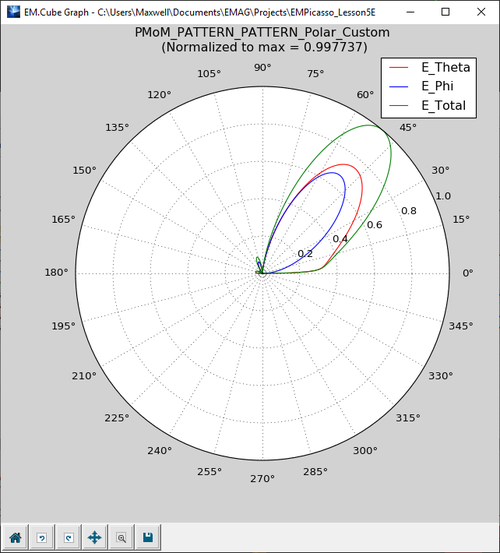
Besides the 2D radiation patterns in the principal XY, YZ and ZX planes, EM.Picasso also computes the 2D radiation pattern graphs in one additional Phi plane cut. This is called the "Custom" Phi plane cut and its default φ value is 45°. Open the Data Manager and plot the data files "FF_1_PATTERN_Cart_Custom.DAT" and "FF_1_PATTERN_Polar_Custom.DAT" as shown in the figures below.
Building a Finite-Sized Probe-Fed Patch Array
To build a finite-sized patch array, use the Probe-Fed Patch Array Wizard ![]() to create a default 2 × 2 patch array first.
to create a default 2 × 2 patch array first.
Then, open the variables dialog and change the values of the parameters "nx" and "ny" to 4. Also, make other changes according to the table below:
| Variable Name | Original Definition | New Definition |
|---|---|---|
| er | 2.2 | 3.38 |
| h | 0.0015*to_meters | 1.524 |
| len | 0.48*lambda0_unit/sqrt(er) | 52 |
| feed_rad | 0.0025*to_meters | 1 |
| feed_x | feed_ratio*len | 15 |
| nx | 2 | 4 |
| ny | 2 | 4 |
| spacing | 0.5*lambda0_unit | 95 |
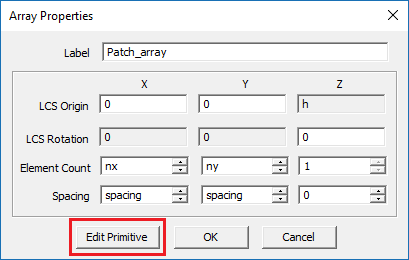
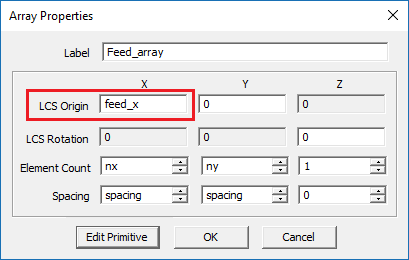
The patch array you just created is a finite-sized rectangular grid configuration of the probe-fed patch antenna you analyzed earlier. The wizard automatically generates an array object called "Patch_array" out of a key element, which is a single probe-fed patch antenna in this case. The initial key object is called the "primitive" and becomes part of the newly created array object. You can change the array properties including its number of elements and element spacings along the three principal directions. You can also access the properties of the primitive and modify them as well. Once you change the primitive, all the other elements of the array object are automatically updated accordingly. Note that the inter-element spacing in both X and Y directions has been set equal to a variable called "spacing", defined to have a value of half the free-space wavelength.
Make the changes for "Feed_array" shown in the figure below:
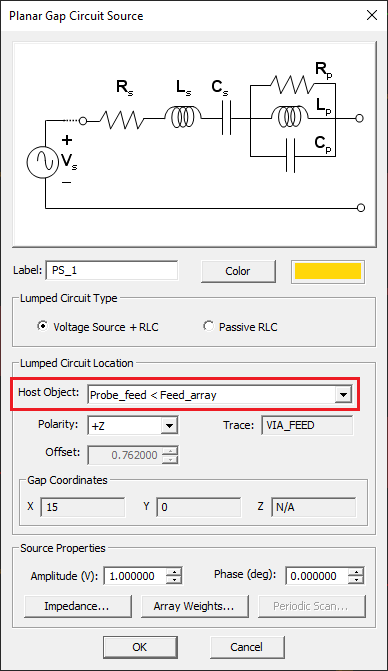
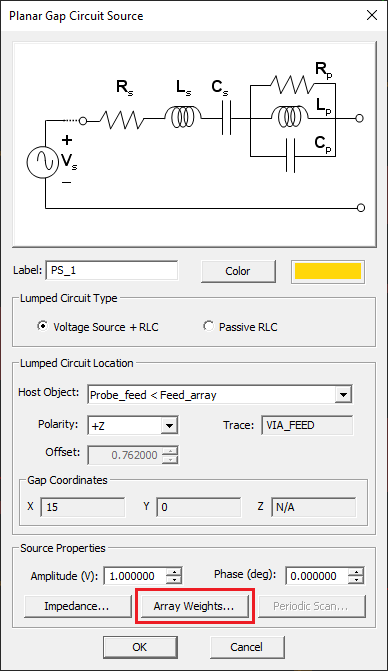
Each patch element is excited using a probe feed. The feed sources are located on an array of PEC Via objects called "Feed_array". Just as you can place a probe source on a PEC via object (as you did in Tutorial lesson 4), you can place an array of probe sources on a PEC via array subject to the same limitations. The wizard automatically created a probe source array and associated it with "Feed_array" as you can see from its property dialog:
The wizard also initiated a far-field radiation pattern observable with theta and phi angle increments both equal to 1°. Since the radiation pattern of antenna arrays usually involve multiple side lobes and nulls, a better resolution is needed than the default value of 5°. However, the wizard doesn't insert a port definition by itself. Note that in the case of your 4 × 4 patch array, this means a 16 × 16 scattering matrix.
| |
Instead of using a wizard, you could have used EM.Cube's Array Tool to create an array of rectangle strip objects along with an array of embedded PEC via objects to construct your probe-fed patch antenna array. |
Running a PMOM Analysis of the Finite-Sized Patch Array
Generate and view the mesh of the patch array and make sure it is consistent. Checkmark the "Simplify Mesh of Small Vias" checkbox.
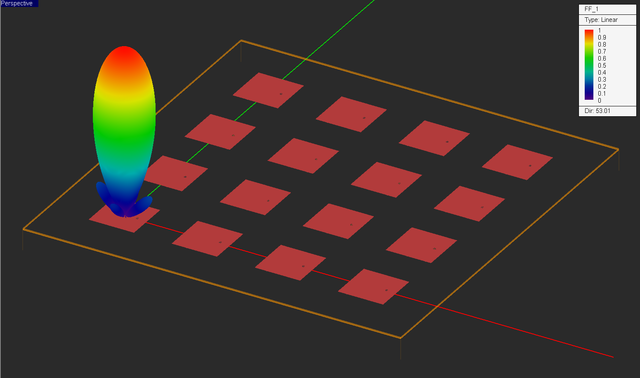
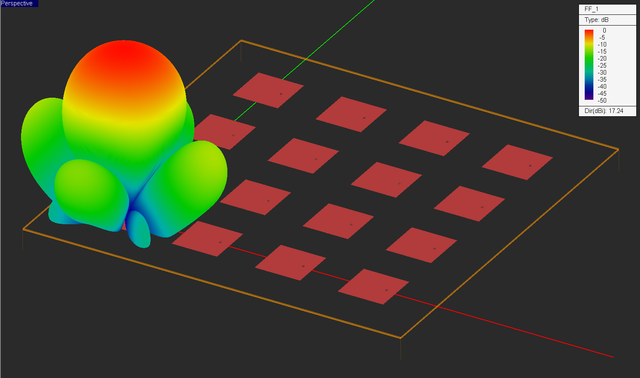
EM.Picasso's PMOM simulator solves a dense linear system. For matrix sizes greater than N = 5,000, iterative solvers like bi-conjugate gradient (BiCG) are more effective than the direct solvers like LU. The PMOM engine's default Automatic Solver option picks the right solver for a given problem. Run a quick PMOM analysis of your 4×4 patch array. In this case, N = 7,552. The BiCG loop will converges after 446 iterations. At the end of the simulation, visualize the current distribution and 3D radiation pattern of your antenna.
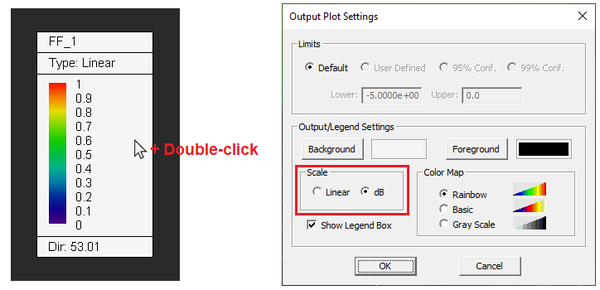
Sometimes it is preferred to plot the radiation patterns on a dB scale. To do so, double-click on the legend to open up the Output Plot Settings dialog. You can also open this dialog from the contextual menu of the total 3D radiation pattern item in the navigation tree. In the Scale section of the dialog, select the "dB" radio button. The directivity is now displayed on the dB scale: D0 = 17.24dB.
Shaping the Beam of the Finite-Sized Patch Array
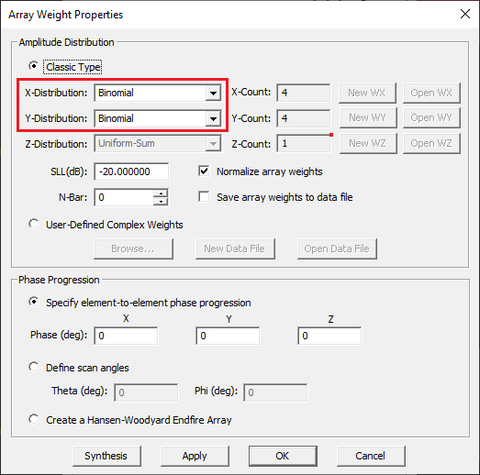
In the previous part of this lesson, we assumed the all the 16 patch elements were excited using identical probe sources. In other words, the amplitudes and phases of all the 16 lumped sources were assumed to be equal, hence, a uniform weight distribution. EM.Picasso allows you to define different weights for individual elements of a source array. Open the property dialog of the probe source "PS_1" and click the button labeled Array Weights.... In the array weight dialog, the Distribution drop-down list gives a number of options: Uniform, Binomial, Chebyshev and Custom. Uniform distribution is the default option as you used in the previous part of this tutorial lesson. Now select "Binomial" for a radiation pattern with minimal side lobes. Close the array weights dialog and then close the lumped source dialog to return to the project workspace.
Run a new PMOM analysis of your weighted finite-sized antenna array and visualize its near fields. The linear system still has the same size N = 7,552. However, it takes the solver only 343 BiCG iterations to converge. As you would expect from a binomial distribution, the interior elements are hotter than the exterior elements.
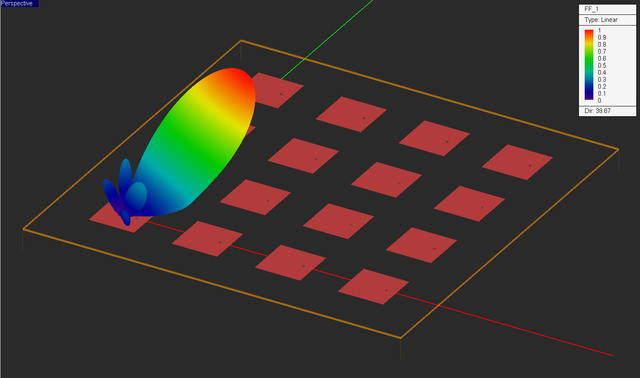
Next, visualize the 3D radiation pattern of the array. The directivity of the 4 × 4 patch array has now reduced to D0 = 33.63, but the side lobe have completely disappeared as you would expect from the antenna array theory.
Steering the Beam of the Finite-Sized Patch Array
Just as you can steer the beam of an infinite periodic array, you can also steer the beam of a finite-sized antenna array. This can be done from the source array dialog. Open the property dialog of the source array "PS_1" and click the button labeled Array Weights.... Change the Distribution back to the Uniform type. At the bottom of this dialog, you will see zero default values for the "Phase Progression" along the X, Y and Z directions. In the case of beam steering, your planar array's elements must have a nonzero phase progression along the X and Y directions. Earlier you found that to steer the beam of the array to θ = φ = 45°, you need equal phase progressions of -90° along both X and Y directions. Enter a value of -90 in the respective boxes of the source array dialog.
Run a new PMOM analysis of your array with a uniform amplitude distribution and phase progressions of -90°. Note that the mesh of the structure does not change due to the changes in the source definition. The linear system still has the same size N = 7,552. However, you will notice that the steered beam case would take 749 BiCG iterations and much longer time to converge. Visualize the current distribution and 3D radiation pattern of the array.
Similar to the periodic array case with beam steering, plot the 2D Cartesian and polar graphs for the custom φ = 45° plane cut.
Examining the Phase of the Radiating Elements
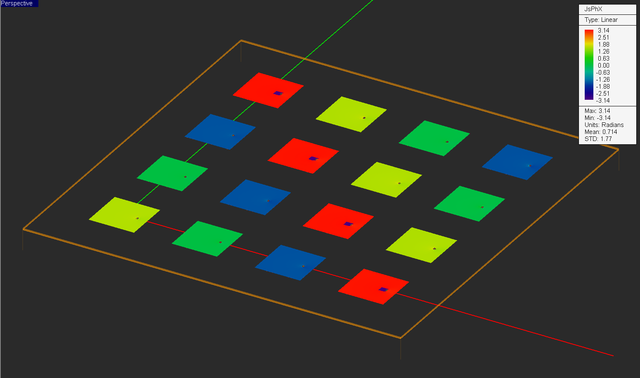
So far you have been mostly interested in the total current distribution maps. EM.Picasso also plots the phase distributions of all the three components of the electric and magnetic surface current. The figure below shows the phase distribution of Jx on the patch array plane. This plot is called "JsPhX" in the navigation tree. The phase progression among the patch elements is clearly visible from the plot.