What You Will Learn
In this tutorial you will learn about another type of magnetic source called wire current, which is used to model thin current-carrying wires with arbitrary curved shapes. You will use wizards to create solenoids and toroidal coil objects. You will also learn about EM.Cube's variables as well as CubeCAD's versatile curve generator.
Getting Started
Open the EM.Cube application and switch to EM.Ferma. Start a new project with the following parameters:
A Note on EM.Ferma's Current Source Types
EM.Ferma's magnetostatic simulation enginge solves the magnetic Laplace or Poisson equation for the magnetic vector potential using the finite difference (FD) method. The general form of these equations is given by:
[math]\Delta \mathbf{A} (\mathbf{r}) = \nabla^2 \mathbf{A}(\mathbf{r}) = - \mu \mathbf{J}(\mathbf{r}) [/math]
where A(r) is the magnetic vector potential, J(r) is the volume current density, and μ = μr μ0 is the permeability of the medium. The magnetic Poisson equation is vectorial in nature and involves a system of three scalar differential equations corresponding to the three components of A(r).
EM.Ferma offers two types of current sources:
- Volume Currents
- Wire Currents
A volume current group is characterized by the three components of the current density vector, Jx, Jy and Jz, having units of A/m2. You learned about volume current sources in Tutorial Lesson 4. Under a volume current group, you can draw any solid geometric objects such as box, cylinder, cone, etc. A wire current is used to approximate a current filament, that is a current source flowing through a line or curve with a specified finite radius. A wire current group is characterized by its total current (I) having units of Amperes. In EM.Ferma, only line and polyline objects can support wire currents. Under a wire current group, you can define any curve geometric object. However, before running a magnetostatic simulation, the program warns that all the curve object will be polygonized and replaced with polyline objects.
Since the governing differential equations only recognize the volume current density J, and not I, as a valid source, EM.Ferma takes the linear current along a wire current source and converts it to a volume current density defined as
[math] \mathbf{J(r)} = \frac{I}{\pi a^2} \mathbf{\hat{u}_0} [/math]
where a is the radius of the wire and u0 is its direction vector. Therefore, there is an inherent crude approximation involved in this type of modeling, which may become more pronounced when the wires are highly curved and not aligned along the three principal axes.
Creating a Solenoid Geometry
Solenoids are used to generate a uniform magnetic field. You can model a solenoid in EM.Ferma using a helix curve object. In this tutorial, however, you will use a wizard to create a solenoid geometry.
Click on the Solenoid Wizard ![]() button of the Wizard Toolbar or select the menu item Tools → Component Wizards → Solenoid.
button of the Wizard Toolbar or select the menu item Tools → Component Wizards → Solenoid.
The geometry of an upright solenoid with a circular cross section appears at the center of the project workspace. The name of the new object called "coil" is added under a new group item called "WIRE_CURRENT" in the navigation tree.
If you zoom in the new solenoid, you will see a large number of arrows (or cones) placed all over the object. The new object "coil" is indeed a polyline object. When a line or polyline object is added under a wire current group, each segment of the line or polyline gets an arrow which shows the direction of flow of the current.
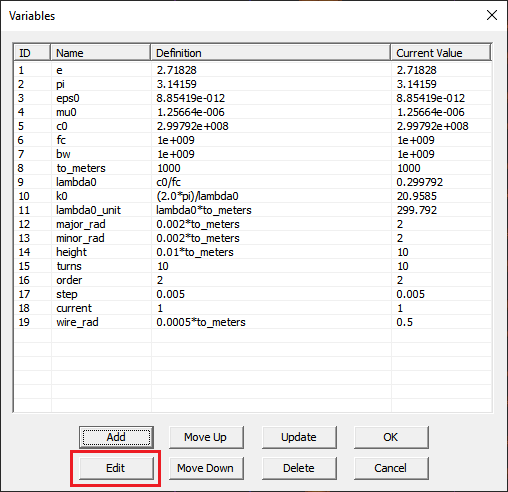
Open the property dialog of the wire current group and examine its parameters. You will see the words "current" and "wire_rad" in boxes that normally take numeric values. These are variables that have been defined by the wizard.
The geometry of the solenoid object created by the wizard is fully parameterized. Open EM.Cube's Variable Dialog by clicking the ![]() button on the Simulate Toolbar or selecting the menu item Simulate → Variables.... In this dialog, you will see a list of all the variables that have been used for the definition of the solenoid object. These parameters can easily be changed to any arbitrary value, expression, or other definitions.
button on the Simulate Toolbar or selecting the menu item Simulate → Variables.... In this dialog, you will see a list of all the variables that have been used for the definition of the solenoid object. These parameters can easily be changed to any arbitrary value, expression, or other definitions.
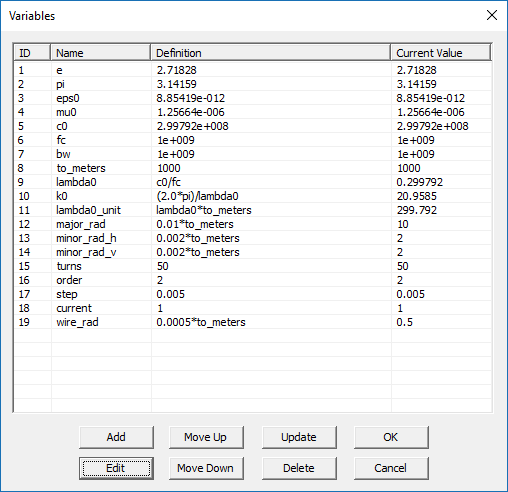
Change the value of some of these variables according to the table below:
| Variable Name | Original Definition | New Definition |
|---|---|---|
| major_rad | 0.002*to_meters | 5 |
| minor_rad | 0.002*to_meters | 5 |
| height | 0.01*to_meters | 50 |
| turns | 10 | 50 |
| wire_rad | 0.0005*to_meters | 0.125 |
To change the definition of a variable, select and highlight it in the variables list and click the Edit button of the dialog. A new "Edit Variable" dialog opens up. In the box labeled Definition, replace the old numeric value or expression with a new one. The figure below shows how to change the definition or value of the variable "major_rad":
After making all the above changes, the variables dialog should look like this:
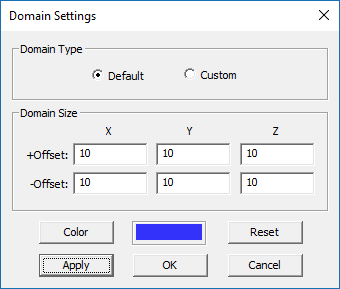
Also, open the domain settings dialog and change the value of the domain offset to 10mm in all the six directions:
The geometry of your solenoid should now look like this:
Examining the Geometry of the Parametric Curve
The wizard used CubeCAD's Curve Generator to create a parametric curve to model the solenoid object. In this case, your solenoid is indeed a helix curve. However, the wizard's definition gives a more generalized helical coil object with Super-Quadratic cross section. Right-click on the name of your solenoid in the navigation tree and select Properties... from the contextual menu. This opens up the "Curve Generator" dialog as shown in the figure below:
The x, y and z coordinates of the points on the curve are defined as functions of parameter "t", which varies from a Start Value of 0 to a Stop Value of 2π. The expressions used for the definition of the coordinates X(t), y(t) and z(t) involve two Python functions msin(x,r) and mcos(x,r). These preloaded Python functions are listed in EM.Cube's functions list. EM.Cube provides a large set of advanced mathematical function as Python libraries or modules. To open this list, click the Functions ![]() button of the Simulate Toolbar or select the menu item Simulate → Functions....
button of the Simulate Toolbar or select the menu item Simulate → Functions....
The definition of the three coordinate functions X(t), y(t) and z(t) also involves variables like "major_rad", "minor_rad", "height", etc. which you saw earlier in the variables dialog. To preserve the parameterization of your solenoid object, you should change its properties from the variables dialog rather than directly from its property dialog.
Running a Magnetostatic Analysis of the Solenoid
Note that the wizard also defines two orthogonal, vertical, X- and Y-directed field sensor planes called "FSX" and "FSY", respectively. Change the settings of these observables as follows:
| Field Sensor | Direction | Coordinates | Plot Type | Max. Size | Cone Length Ratio | Cone Radius Ratio |
|---|---|---|---|---|---|---|
| FSX | X | (0, 0, 0) | Intensity | - | - | - |
| FSY | Y | (0, 0, 0) | Vector | 0.5 | 0.75 | 0.25 |
In accordance with the introduction of this tutorial lesson, open the mesh settings dialog and change the value of the fixed mesh cell size to Δx = Δy = Δz = √2(2a) = √2(2*0.125) = 0.35mm.
Run a magnetostatic simulation of your structure and visualize the field sensor plots. You can Hide any geometric objects to see other objects hidden behind, beneath or inside it. To hide an object, right-click on its surface in the project workspace or right-click on its name in the navigation tree and select Hide from the contextual menu. To show the object right-click on its surface in the project workspace or right-click on its name in the navigation tree and select Show from the contextual menu.
Open the data manager and plot the data file "FSX_Z_HTotal.DAT" as shown in the figure below. As you can see from this figure, the magnetic field along the central axis of the solenoid is almost constant (1191A/m) inside the solenoid in the region 12mm ≤ z ≤ 36mm.
These results can be verified by considering the case of a infinitely long solenoid. Using Ampere's law, one can show that the magnetic field of the solenoid is directed along its axis (Z-axis) and given by:
[math] H_z = N_TI [/math]
where NT is the number of solenoid turns per unit length. Your helical object has 50 turns and a height of 50mm. Therefore, NT = 1000 turns/m, and the magnetic field of an infinitely long version of your solenoid is found to be:
[math] H_z (z = 25mm) = (1000)(1A) = 1000 A/m [/math]
Building & Analyzing a Toroidal Coil
You may want to start a new blank project for this part of the tutorial lesson. You are going to create the geometry of a toroidal coil using one of EM.Cube's convenient wizards. To do so, click on the Coil Wizard ![]() button of the Wizard Toolbar or select the menu item Tools → Component Wizards → Toroidal Coil.
button of the Wizard Toolbar or select the menu item Tools → Component Wizards → Toroidal Coil.
The geometry of a toroidal coil with a circular cross section appears at the center of the project workspace, and its name is added under a new group item called "WIRE_CURRENT" in the navigation tree. The wire current group has the same properties as in the last part.
The geometry of the toroidal coil object created by the wizard is fully parameterized. Open Variables Dialog and review the list of all the variables that have been used for the definition of the toroidal helix object.
Change the value of some of these variables according to the table below:
| Variable Name | Original Definition | New Definition |
|---|---|---|
| major_rad | 0.01*to_meters | 15 |
| minor_rad_h | 0.002*to_meters | 5 |
| minor_rad_v | 0.002*to_meters | 5 |
| step | 0.005 | 0.0025 |
| turns | 50 | 100 |
| wire_rad | 0.0005*to_meters | 0.125 |
After making all the above changes, the variables dialog should look like this:
Similar to the previous part, set the domain offset equal to 10mm in all the six directions. Also, open the mesh settings dialog and set the fixed mesh cell size to Δx = Δy = Δz = 0.35mm. The geometry of your toroidal coil should now look like this:
The figure below shows the fixed-cell mesh of your coil structure:
Open the property dialog of your coil object and examine the definition of toroidal coil in Curve Generator. The parameter "major_rad" determines the major radius of the torus. The cross section of this curve in a generalized super-quadratic curve with two horizontal and vertical radii: "minor_rad_h" and "minor_rad_v". The parameter t varies from zero to 2π. For this project, you reduced the value of the variable "step" to 0.0025 to create a smoother polyline.
Note that the wizard also defined three orthogonal, vertical, X-, Y- and Z-directed field sensor planes called "FSX", "FSY" and "FSZ", respectively. Change the settings of these observables as follows:
| Field Sensor | Direction | Coordinates | Plot Type | Max. Size | Cone Length Ratio | Cone Radius Ratio |
|---|---|---|---|---|---|---|
| FSX | X | (0, 0, 0) | Intensity | - | - | - |
| FSY | Y | (0, 0, 0) | Vector | 1 | 0.5 | 0.25 |
| FSZ | Z | (0, 0, 0) | Vector | 1 | 0.5 | 0.25 |
Run a magnetostatic simulation of your structure and visualize the field sensor plots. You can see a fairly uniform azimuthal magnetic field at the center of the coil.