Analog Tutorial Lesson 7: Designing Active Sullen-Key Filters
Contents
What You Will Learn
In this tutorial you will design second-order lowpass, highpass and bandpass Sallen-Key active filters using an operational amplifier, resistors and capacitors. You will also learn how to define custom plots.
Designing a Second-Order Active Lowpass Filter
The following is a list of parts needed for this part of the tutorial lesson:
| Part Name | Part Type | Part Value |
|---|---|---|
| VCC | DC Voltage Source | 15V |
| VEE | DC Voltage Source | -15V |
| V1 | AC Voltage Source | 1V |
| R1 | Resistor | 10k |
| R2 | Resistor | 10k |
| C1 | Capacitor | 22.5n |
| C2 | Capacitor | 11.25n |
| X1 | LM741 Op-Amp | Defaults |
The basic second-order lowpass Sallen-Key active filter is shown in the above figure. The transfer function of this filter is given by:
[math]H(j\omega) = \frac{V_{out}} {V_{in}} = \frac {1} {1-\omega ^2 R_1 R_2 C_1 C_2 + j\omega C_2 \left( R_1 + R_2 \right) } [/math]
Setting s = jω, one can write:
[math]H(s) = \frac {\omega_0 ^2} {s^2 + s(\omega_0 / Q) + \omega_0 ^2} = \frac {\omega_0 ^2} { \left( s - s_1 \right) \left( s - s_2 \right) } [/math]
where
[math]\omega_0 = \frac {1}{\sqrt{ R_1 R_2 C_1 C_2 } }[/math]
[math]Q = \sqrt{\frac{C_1}{C_2}} \left( \frac{\sqrt{ R_1 R_2 }}{R_1 + R_2} \right) [/math]
The poles are given by:
[math]s_1 = -\frac {\omega_0}{2Q} + \sqrt{ \left( \frac {\omega_0}{2Q} \right) ^2 - \omega_0 ^2 } [/math]
[math]s_2 = -\frac {\omega_0}{2Q} - \sqrt{ \left( \frac {\omega_0}{2Q} \right) ^2 - \omega_0 ^2 } [/math]
These expressions can be further simplified by setting R1 = R2 = R. Then we have:
[math]\omega_0 = \frac {1}{R \sqrt{ C_1 C_2 } }[/math]
[math]Q = \frac{1}{2} \sqrt{\frac{C_1}{C_2}} [/math]
To design a lowpass filter with a cutoff frequency of f0 = ω0 / 2π = 1kHz and a maximally flat Q = 1/√2, and assuming R1 = R2 = R = 10k, the above equations yield C1 = 2Q/(ω0R) = 22.5nF and C2 = 1/(2Qω0R) = 11.25nF. Place and connect the parts with the specified values as shown in the above figure. Place two voltage probe markers labeled "IN" and "OUT" at the input and output of the filter, respectively.
To characterize your active filter, you will run an AC Sweep Test. Open the Test Panel of the Toolbox and define the start and stop frequencies of the AC frequency sweep as 1Hz and 50kHz, respectively. For this sweep, choose the "Decade" interval options with 50 Steps / Interval. Before you run your AC sweep, you will specify a custom plot for the simulation. This will be the gain of the filter defined as Vout / Vin expressed in the dB scale. For this purpose, click the "Preset Graph Plots..." button of the Test Panel to open up the "Edit Plot List" dialog. You will see that VDB(OUT) and VDB(IN) are already listed as the plots to be generated. Remove these plots from the list using the left arrow button. Instead, click the "Add Custom Plot" button to open up the "Edit Signal Plot" dialog. Define a new signal called "Gain" with the "Yellow" color and define as "VDB(OUT) - VDB(IN)" as shown in the figure below.
| Start Frequency | 1Hz |
|---|---|
| Stop Frequency | 50kHz |
| Steps/Interval | 50 |
| Interval Type | Decade |
| Preset Graph Plots | Custom: Gain = VDB(OUT) - VDB(IN) |
Run an AC frequency sweep of your active filter. You should get a frequency response like the figure shown below. As you would have expected, the 3dB knee of the curve is located at 1kHz. From the graph you can see that at f = 5kHz, the gain drops to -28dB.
Designing a Second-Order Active Highpass Filter
The following is a list of parts needed for this part of the tutorial lesson:
| Part Name | Part Type | Part Value |
|---|---|---|
| VCC | DC Voltage Source | 15V |
| VEE | DC Voltage Source | -15V |
| V1 | AC Voltage Source | 1V |
| R1 | Resistor | 11.25k |
| R2 | Resistor | 22.5k |
| C1 | Capacitor | 10n |
| C2 | Capacitor | 10n |
| X1 | LM741 Op-Amp | Defaults |
The basic second-order lowpass Sallen-Key active filter is shown in the above figure. The transfer function of this filter is given by:
[math]H(j\omega) = \frac{V_{out}} {V_{in}} = \frac {(j\omega)^2 R_1 R_2 C_1 C_2} {1-\omega ^2 R_1 R_2 C_1 C_2 + j\omega R_1 \left( C_1 + C_2 \right) } [/math]
Setting s = jω, one can write:
[math]H(s) = \frac {s^2} {s^2 + s(\omega_0 / Q) + \omega_0 ^2} = \frac {s^2} { \left( s - s_1 \right) \left( s - s_2 \right) } [/math]
where
[math]\omega_0 = \frac {1}{\sqrt{ R_1 R_2 C_1 C_2 } }[/math]
[math]Q = \sqrt{\frac{R_2}{R_1}} \left( \frac{\sqrt{ C_1 C_2 }}{C_1 + C_2} \right) [/math]
The same definitions of the poles s1 and s2 given earlier for the case of the lowpass filter are still valid for this case, too. The above expressions can be further simplified by setting C1 = C2 = C. Then we have:
[math]\omega_0 = \frac {1}{C \sqrt{ R_1 R_2 } }[/math]
[math]Q = \frac{1}{2} \sqrt{\frac{R_2}{R_1}} [/math]
To design a highpass filter with a cutoff frequency of f0 = ω0 / 2π = 1kHz and a maximally flat Q = 1/√2, and assuming C1 = C2 = C = 10nF, the above equations yield R2 = 2Q/(ω0C) = 22.5k and R1 = 1/(2Qω0C) = 11.25k. Place and connect the parts with the specified values as shown in the above figure. Run an AC frequency sweep of your active filter. You should get a frequency response like the figure shown below with a cutoff frequency of 1kHz.
| Start Frequency | 1Hz |
|---|---|
| Stop Frequency | 50kHz |
| Steps/Interval | 50 |
| Interval Type | Decade |
| Preset Graph Plots | Custom: Gain = VDB(OUT) - VDB(IN) |
Designing a Second-Order Active Bandpass Filter
The following is a list of parts needed for this part of the tutorial lesson:
| Part Name | Part Type | Part Value |
|---|---|---|
| VCC | DC Voltage Source | 15V |
| VEE | DC Voltage Source | -15V |
| V1 | AC Voltage Source | 1V |
| R1 | Resistor | 11.25k |
| R2 | Resistor | 22.5k |
| C1 | Capacitor | 10n |
| C2 | Capacitor | 10n |
| X1 | LM741 Op-Amp | Defaults |
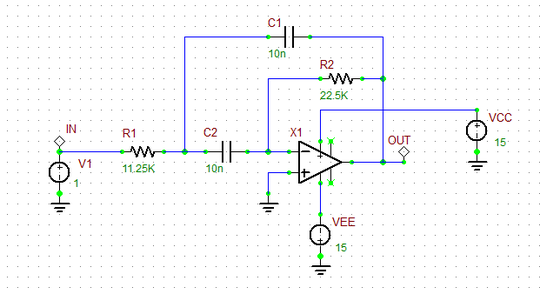
The basic second-order bandpass Sallen-Key active filter is shown in the above figure. The transfer function of this filter is given by:
[math]H(j\omega) = \frac{V_{out}} {V_{in}} = \frac {(j\omega)^2 R_1 R_2 C_1 C_2} {1-\omega ^2 R_1 R_2 C_1 C_2 + j\omega R_1 \left( C_1 + C_2 \right) } [/math]
Setting s = jω, one can write:
[math]H(s) = \frac {-\omega_0 ^2 R_2 C_2 s} {s^2 + s(\omega_0 / Q) + \omega_0 ^2} = \frac {-\omega_0 ^2 R_2 C_2 s} { \left( s - s_1 \right) \left( s - s_2 \right) } [/math]
where
[math]\omega_0 = \frac {1}{\sqrt{ R_1 R_2 C_1 C_2 } }[/math]
[math]Q = \sqrt{\frac{R_2}{R_1}} \left( \frac{\sqrt{ C_1 C_2 }}{C_1 + C_2} \right) [/math]
The same definitions of the poles s1 and s2 given earlier for the case of the lowpass filter are still valid for this case, too. The above equations represent a biquad transfer function with one zero and two poles.
In particular, at the passband center frequency &omega0, we have:
[math] \left| H(j\omega_0) \right| = \left| \frac{V_{out}} {V_{in}} \right|_{\omega =\omega_0} = \frac {R_2 C_2} { R_1 \left( C_1 + C_2 \right) } = \sqrt{ \frac{R_2 C_2}{R_1 C_1} }Q [/math]
The half-power bandwidth of the filter is defined as BW = ω2 - ω1. It can be shown that for large Q values, BW ≅ ω0 / Q. The above expressions can be further simplified by setting C1 = C2 = C. Then, you will get the same relationships as in the highpass case:
[math]\omega_0 = \frac {1}{C \sqrt{ R_1 R_2 } }[/math]
[math]Q = \frac{1}{2} \sqrt{\frac{R_2}{R_1}} [/math]
At the passband center frequency &omega0, you will have:
[math] \left| H(j\omega_0) \right| = \left| \frac{V_{out}} {V_{in}} \right|_{\omega =\omega_0} = \frac{1}{2} \frac {R_2} {R_1} [/math]
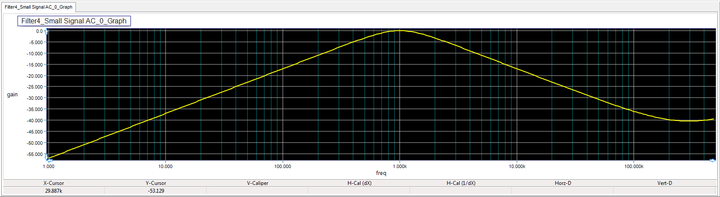
In this part of the tutorial lesson, you will design a bandpass filter with a center frequency of f0 = ω0 / 2π = 1kHz and a maximally flat Q = 1/√2. Assuming C1 = C2 = C = 10nF, the above equations yield R2 = 2Q/(ω0C) = 22.5k and R1 = 1/(2Qω0R) = 11.25k . Place and connect the parts with the specified values as shown in the above figure. Run an AC frequency sweep of your active filter. But this time set the stop frequency of the sweep to 500kHz. You should get a frequency response like the figure shown below with a passband center frequency of 1kHz. Note that at 1kHz, the gain is 0dB because |H(jω0)| = R2/(2.R1) = (22.5k) / (2)(11.25k) = 1.
| Start Frequency | 1Hz |
|---|---|
| Stop Frequency | 500kHz |
| Steps/Interval | 50 |
| Interval Type | Decade |
| Preset Graph Plots | Custom: Gain = VDB(OUT) - VDB(IN) |